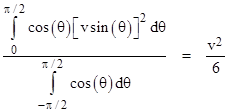Kinetic Pressure and Tetrode’s Star

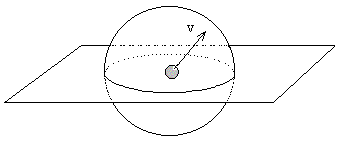
As discussed in another note, the outward pressure on the walls of a container due to elastic collisions of kinetic particles within the container can be deduced from the time intervals between successive reflections of the particles off the walls. This derivation strictly applies only to enclosed regions. A more direct derivation, and one not restricted to enclosed regions, can be given by simply evaluating the average momentum, normal to a given plane, of particles passing through that plane. In general, each particle is assumed to have a direction of motion taken from a spherically uniform distribution, as depicted below:

If every particle was moving directly upward (normal to the surface) with speed v, the rate of momentum flow per unit area through the surface would be ρv² where ρ is the mean volumetric density of the flux of particles. To determine the mean momentum flux upward normal to the surface, we integrate the square of the vertical component over the upper hemisphere, divided by the integral of unity over the entire sphere, which gives

Likewise the mean squared speed in the downward normal direction is v²/6. Now, if we imagine a solid elastic surface forming a boundary of the uniform flux of particles, this surface must be absorbing momentum per unit area of ρv²/6 from the incoming particles, and imparting ρv²/6 to the outgoing particles. Hence the total pressure on the surface equals ρv²/3.

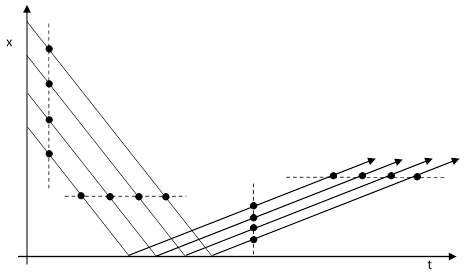
In the late 1680s Nicholas Fatio attempted to reconcile the Cartesian insistence on contact forces and the Newtonian theory of gravitation by positing a radiation field of imperceptibly small particles, moving at high speed in all directions, throughout space. He also supposed that the collisions are somewhat inelastic, so those particles rebounding from collisions with ordinary matter have a lower speed than when they approached. It’s interesting that, in 1690, Fatio said he had been “detained” for three years by uncertainty over whether the flux surrounding an ordinary body would really exert a net inward force. The outward-going particles would be moving more slowly, but Fatio realized they would also be closer together, and he wasn’t sure if this might compensate for the slower speed. The situation is illustrated for one spatial dimension in the figure below:

The reflected particles are indeed more closely spaced than the incident particles, as shown by the closer spacing in the vertical direction, but the time interval between successive particles is the same for the incident and reflected particles, as shown by the horizontal distributions. In retrospect we can see Fatio’s uncertainty was due to confusion over the concepts of force, momentum, and kinetic energy. In a sense he anticipated the 18th century dispute over the concepts of vis viva and vis mortua. Recall that one of Galileo’s greatest accomplishments was his recognition that the speed of falling bodies increases linearly with time, not with distance. Thus v = g Δt and so v²/2 = g Δs. In Newtonian terms, the force of gravity on an object of mass m is F = mg, so multiplying through these two relations by m, we get

Thus the integral of force with respect to time represents momentum, whereas the integral of force with respect to distance represents (kinetic) energy. Both Descartes and Newton tended to regard the “quantity of motion” of a falling object as being proportional to the time of fall (from rest), whereas Leibniz and his followers argued (in effect) that the “true” measure of the “quantity of motion” is proportional to the distance fallen.  This dispute can be seen as an argument over whether the conservation of momentum or the conservation of energy is more fundamental. Today these conservation laws have been consolidated (as have the concepts of space and time), so energy and momentum are seen as simply different components of a single four-vector in space-time.

Eventually, by about 1690, Fatio concluded that the pressure represented by the reflected particles was indeed less than the pressure of the incident particles, assuming the reflection was inelastic, so the reflected particles move more slowly than the incident particles. Of course, this implies that the collisions convey not just momentum (vis mortua), but also kinetic energy (vis viva). From this standpoint, it could be said that Fatio’s uncertainty was related to the thermodynamic objection to Fatio’s theory raised by Thomson and Maxwell nearly two hundred years later, in the late 19th century.

From a historical standpoint, the concept that the universe might be filled with small irreducible particles streaming ceaselessly through the void of space goes back to the origin of atomistic theories in ancient times, but the Fatio-Lesage model of gravitation represented one of the first attempts to apply Newton’s quantitative dynamics to this conception. In this respect it was a forerunner of the later kinetic theory of gases. Indeed, as noted above, Fatio’s expression for the pressure exerted by the gravitational corpuscles moving with speed v was identical – except for a factor of 2 – to the equation for the pressure of a gas whose molecules are moving with a mean speed v. Of course, Newton had already (in the Scholium at the end of Part 1 of Book 2 of the Principia) explained that the inertial force exerted by a fluid with relative speed v and density ρ is proportional to ρv², so it only remained to determine the coefficient to account for the oblique angles of incidence of  particles moving in all directions. Fatio got this coefficient wrong (by underestimating the impulse of reflections), so his contribution to the technical development of kinetic theory of gases was negligible, being limited to, at most, providing an early effort for others (like Bernoulli) to criticize and correct.

On the other, the idea that gravity might be explained by streams of small corpuscles moving in all directions through empty space served to attract the interest of several later scientists to this atomistic conceptual framework, loosening the grip of the Cartesian doctrine of continuous matter. It’s certainly true that some of the scientists who actually contributed significantly to the development of the kinetic theory of gases were originally drawn to the subject by their interest in it as a possible mechanical explanation of gravity and/or the other forces of nature. This is similar to how the modern disciplines of both fluid mechanics and the mechanics of solids were developed largely as by-products of attempts to model the elementary forces of nature in terms of flows, stresses, and strains in such continuous media.

However, it must also be noted that the flux of ultramundane corpuscles in the Fatio-Lesage model differs in many important respects from a gas. The real beginning of the kinetic theory of gases, in the sense of an independent discipline rather than just a handful of trivial deductions from Newton’s laws, came with the introduction of the Maxwell distribution for the velocities of molecules of a gas at equilibrium. The existence of equilibrium implies a thorough-going interaction between the molecules. All the non-trivial aspects of kinetic theory and the associated thermodynamics follow from this premise. In contrast, the corpuscles of Fatio and Lesage are necessarily not in equilibrium, at least not in the vicinity and on the scale of the observable matter of the universe, because if the corpuscles were in thermodynamic equilibrium with ordinary matter, there would be no net force of gravity. Both Fatio and Lesage recognized this, because they stipulated that the corpuscles originate from “beyond the world”, i.e., outside the world of ordinary matter. The very name “ultramundane” coined by Lesage makes it clear that the corpuscles are not in equilibrium with ordinary matter. It’s conceivable that they are at equilibrium with themselves on some cosmological scale, but only if ordinary matter occupies just a finite “island” in an infinite universe. In either case, the implication is the same: According to Fatio-Lesage, gravity is powered by an infinite supply of disequilibrium from “beyond the world” of ordinary matter. The proposed intervening mechanism is really just a secondary aspect of the theory, serving mainly to distract attention from the fundamentally occult and ad hoc nature of the posited “explanation”.

Rather than being consider an early (and faulty) version of the kinetic theory of gases, it would actually be more accurate to regard the ultramundane flux of Fatio-Lesage theory as an anticipation of Faraday’s concept of “radiant matter”, and perhaps of collisionless plasma, which is sometimes called a fourth state of matter (distinct from solids, liquids, and gases). Poincare commented on this distinction in his essay on “The Milky Way and the Theory of Gases”, which coincidentally appears immediately following his essay on Lesage gravity in the 1908 book Science and Method.

Before going further we must consider the problem under another aspect. Is the Milky Way, thus constituted, really the image of a gas properly so called? We know that Crookes introduced the notion of a fourth state of matter, in which gases, becoming too rarefied, are no longer true gases, but become what he calls radiant matter. In view of the slightness of its density, is the Milky Way the image of gaseous or of radiant matter? A gaseous molecule's trajectory may be regarded as composed of rectilineal segments connected by very small arcs corresponding with the successive collisions. The length of each of these segments is what is called the mean free path… Matter will be radiant when the mean path is greater than the dimensions of the vessel in which it is enclosed, so that a molecule is likely to traverse the whole vessel in which the gas is enclosed without experiencing a collision, and it remains gaseous when the contrary is true.

Although he was referring here to the collection of stars in a galaxy, clearly the identical comments apply to Lesage’s flux of ultramundane corpuscles, which essentially never interact with each other. Lesage himself said that an ultramundane corpuscle could traverse the entire known universe and rarely if ever collide with another corpuscle. (This lack of interaction is necessary in order for the shadowing effect to yield a net gravitational force.) Hence, the ultramundane flux of Fatio and Lesage is more properly called radiant matter, a term invented by Faraday in 1816 to describe extremely rarified collection of particles that essentially never collide with each other (over the scale of interest). Crookes borrowed the term to describe what was later understood to be plasma, i.e., highly ionized gas. (It should be noted, however, that even a collisionless plasma involved interactions between the ions due to their Coulomb fields, so it doesn’t correspond precisely to the Faraday-Crookes notion of radiant matter.) Interestingly, recent work in the field of dusty plasmas (i.e., plasmas in which small grains of dust are suspended) has shown that an inverse-square force of attraction between the dust grains arises due to the Lesage shadowing mechanism involving the slightly inelastic bombardment of the ions.

In the 20th century, the Fatio-Lesage concept of gravity attracted the interest of Richard Feynman, who used it more than once to illustrate various aspects of theoretical models. For example, in a series of public lectures given in 1964, published as “The Character of Physical Law” in 1965, Feynman described Fatio’s model as an example of the kind of theory that might satisfy someone’s desire for an “explanation” – rather than just a description – of gravity. Feynman’s notion of a mechanism was something that “gets rid of the mathematics”. For example, regarding the Newtonian mathematical formula F = Mm/r² which described the force of attraction of the sun on a planet, Feynman asks rhetorically

What does the planet do? Does it look at the sun, see how far away it is, and decide to calculate on its internal adding machine the inverse of the square of the distance, which tells it how much to move?

He then describes Fatio’s model of gravity, in which Newton’s mathematical law is a consequence of a large number of more primitive actions – primitive in the sense that they have mathematically trivial descriptions. Each particle simply moves inertially until colliding with some other object, and then it rebounds according to a very simple law. The inverse-square dependence of the force arises naturally from the geometry of space and the effects of a large number of primitive operations.

Therefore, the strangeness of the mathematical relation will be very much reduced, because the fundamental operation is much simpler than calculating the inverse of the square of the distance. This design, with the particles bouncing, does the calculation.

Feynman goes on to discount this model, on the grounds that it implies unacceptable drag on astronomical bodies, so their stable orbits could not have persisted for so long. (Presumably he regarded this as sufficient allusion, in a popular lecture, to the complicated problem of aberration with the light-speed constraint on the particle speeds.) Then he continues

‘Well’, you say, ‘it was a good one, and I got rid of the mathematics for awhile. Maybe I could invent a better one’. Maybe you can, because nobody knows the ultimate. But up to today, from the time of Newton, no one has invented another theoretical description of the mathematical machinery behind this law which does not either say the same thing over again, or make the mathematics harder, or predict some wrong phenomena. So there is no model of the theory of gravitation today, other than the mathematical form.

This is quite an interesting declaration, for several reasons. First, it seems to very pointedly omit any mention of Einstein’s geometrical model of gravitation. Presumably Feynman would contend that the mathematics of general relativity are “harder”, but this is a questionable contention, because the large-scale macroscopic phenomena of gravitation have whatever complexity they have, regardless of our model. Supposedly Feynman was discussing the possibility that these “hard” high-level phenomena might be the result of a large number of very primitive and mathematically trivial local actions taking place within the geometrical framework of space and time. From this point of view, general relativity is surely an example (maybe the example) of an extremely simple local explanation for the highly complex large-scale phenomena of gravitation. It is (at least arguably) much simpler even than Fatio’s model – not to mention that it has the benefit of logical coherence and consistency with observation, both of which are lacking in Fatio’s model.

It may be worth remembering that Feynman was a proponent of the field interpretation (rather than the geometrical interpretation) of general relativity, so it’s perhaps not surprising that he didn’t refer here to the conceptual simplicity of the geometrical interpretation. On the other hand, the field theoretic view of gravitation in terms of the actions of spin-2 massless “particles” could also be regarded as a primitive mechanism underlying the “hard” mathematics. It’s ironic that Feynman seemed to be so pessimistic about the prospects for primitive models underlying complex phenomena, considering that among his greatest contributions to modern physics were things like Feynman diagrams, the concept of the sum over all paths, and the description of quantum electrodynamics in terms of a simple set of “rules”. In fact, his entire career consisted largely of devising simple models based on very primitive actions, which, in the aggregate, resulted in the phenomena of field theories. In another series of popular lectures, published as the book “QED, The Strange Theory of Light and Matter”, he described three simple actions: (1) a photon goes from place to place, (2) an electron goes from place to place, and (3) an electron emits or absorbs a photon.

It is hard to believe that nearly all the vast apparent variety in Nature results from the monotony of repeatedly combining just these three basic actions. But it does… You might wonder how such simple actions could produce such a complex world. It’s because phenomena we see in the world are the result of an enormous intertwining of tremendous numbers of photon exchanges and interferences.

Compare this with his description of how Fatio’s model leads to the seemingly complicated mathematical law of gravity

There will be an impulse on the earth towards the sun that varies inversely as the square of the distance. And this will be the result of large numbers of very simple operations, just hits, one after the other, from all directions.

So it’s odd that Feynman seems to argue that no one has ever invented a successful way of accounting for the mathematical effects of field theories in terms of a large number of simple actions, such as in the shadowing theory of gravitation. Elsewhere he distinguishes between gravity and the other forces of nature, so perhaps his pessimistic view was limited to explanations of gravity. On the other hand, he applied the example of gravity to all of physics, arguing that all physical laws are irreducibly complicated and mathematical.

The more we investigate, the more laws we find, and the deeper we penetrate nature, the more this disease persists. Every one of our laws is a purely mathematical statement in rather complex and abstruse mathematics… It gets more and more abstruse and more and more difficult as we go on. Why? I have not the slightest idea. It is only my purpose to tell you about this fact.

So his pessimism about the prospects of reducing physics to a simple set of actions seems to apply to all physics, not just gravitation… or at least this is the impression one would get from this part of the book. However, just a few pages later, after describing the general nature of field theories based on local differential equations, and minimal theories based on global integral equations, he confides

It always bothers me that, according to the laws as we understand them today, it takes a computing machine an infinite number of logical operations to figure out what goes on in no matter how tiny a region of space, and no matter how tiny a region of time… so I have often made the hypothesis that ultimately physics will not require a mathematical statement, that in the end the machinery will be revealed, and the laws will turn out to be simple…

Thus after laboring for an entire chapter to convince us that the laws of physics are unavoidably (and increasingly) complex and mathematical, he speculates that they will ultimately be revealed to be simple and non-mathematical. Nevertheless, he concludes by quoting Jeans to the effect that ‘the Great Architect seems to be a mathematician’. Perhaps the best expression of Feynman’s view of the subject is when we says ‘it is good not to be too prejudiced about these things’.

One of the most striking examples of Feynman’s propensity for devising simple conceptual models for seemingly complex theories was the Wheeler-Feynman model of classical electrodynamics. In this model the field is entirely eliminated, and all the observed phenomena, including the effect of ‘propagating waves’, are actually due to direct action-at-a-distance between particles. This idea is quite old, being the theoretical framework for many of the pioneers in electromagnetism, including Coulomb, Ampere, and Weber. In the 20th century, Hugo Tetrode wrote about this approach. According to Tetrode in a paper written in 1922

The sun would not radiate if it were alone in space and no other bodies could absorb its radiation… If for example I observed in my telescope yesterday evening that star which let us say is 100 light years away… the star or individual atoms of it knew already 100 years ago that I, who then did not even exist, would view it yesterday evening at such and such a time.

This idea is sometimes expressed in terms of modern quantum field theory by saying that “every photon is virtual”, i.e., every photon (at least those of which we have any knowledge) is both emitted and absorbed. We have no experience of “free photons”, so ultimately it is possible (if we wish) to eliminate photons from our models, and describe physics entirely in terms of interactions between material particles.

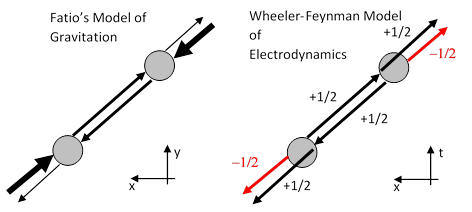
Einstein remembered Tetrode’s writings when he heard Feynman give a talk on the “absorber theory” in Princeton around 1946. The theory of Wheeler and Feynman was called “absorber theory” because it accounted for the radiation reaction on an accelerating charge by supposing that all of the retarded radiation emitted by the charge is ultimately (like the light from Tetrode’s star) absorbed by some distant particles in the future, and this causes those particles to accelerate slightly, resulting in the symmetrical emission of both retarded and advanced radiation. This combines, through constructive or destructive interference, with the half advanced and half retarded radiation from the original particle, yielding as a net result only the fully retarded radiation from the source. There’s an intriguing correspondence between this theory and the Fatio-Lesage model of gravitation, as shown in the two figures below.

In both models, an apparent interaction strictly between two particles is actually just the net result of actions extending far beyond and outside of those two particles. In Fatio’s model, each particle is subject to large forces in both directions, but there is a slight deficit in the force from the direction of the other particle. The large forces cancel out, leaving only an apparent force of attraction between the two particles. Similarly in the Wheeler-Feynman model each particle emits radiation in both directions, but 180 degrees out of phase. The combined radiation streams outside the interval between the two particles cancel out, leaving only an apparent retarded interaction between the particles. I’m not aware that Feynman ever commented on, or even noticed, the parallel between his absorber theory and Fatio’s model of gravitation.

Return to MathPages Main Menu