Controversies Over the Equivalence Principle

In attempting to generalize the (then) restricted theory of relativity in 1907, Einstein was strongly influenced by the evident fact that a person in a gravitational free-fall does not feel their own weight. In other words, for someone falling freely in a gravitational field, it is as if the gravitational field does not exist. This idea, which Einstein called "the happiest thought of my life", is strikingly similar to Galileo's realization (three hundred years earlier) that, for someone moving uniformly in a straight line, it is as if the motion does not exist. This insight of Galileo's was the basis of special relativity, and it's easy to see why Einstein regarded his theory of gravity as a generalization of relativity.

The idea that gravity "does not exist" with respect to a freely falling system of reference was raised by Einstein to the status of a principle, which he called the Equivalence Principle. (Interestingly, just as in the case of the relativity principle itself, the original primitive version of the principle of equivalence was given by Galileo, who argued that all objects undergo the same acceleration due to gravity.) Einstein gave various statements of the equivalence principle over the years, and many other people have proposed interpretations of it as well. Einstein’s original statement of this idea, in his 1907 review article on relativity, was disarmingly simple:

We consider two systems Σ₁ and Σ₂… Let Σ₁ be accelerated in the direction of its X axis, and let γ be the (temporally constant) magnitude of that acceleration. Σ₂ shall be at rest, but it shall be located in a homogeneous gravitational field that imparts to all objects an acceleration –γ in the direction of the X axis. As far as we know, the physical laws with respect to Σ₁ do not differ from those with respect to Σ₂; this is based on the fact that all bodies are equally accelerated in a gravitational field. At our present state of experience we have thus no reason to assume that the systems Σ₁ and Σ₂ differ from each other in any respect, and in the discussion that follows we shall therefore assume the complete physical equivalence of a gravitational field and a corresponding acceleration of the reference system.

An essentially identical statement of the principle of equivalence is given in Einstein’s 1911 paper on the bending of light, where he talks again about a homogeneous gravitational field, and of course he immediately applies this principle to the gravitational field of the Sun, so there can be no doubt that he had in mind “real” gravitational fields produced by masses. In an article on the fundamental ideas of relativity theory, written in 1920, Einstein recalled his epiphany in greater detail:

When I was busy (in 1907) writing a summary of my work on the theory of special relativity, I also had to try to modify the Newtonian theory of gravitation such as to fit its laws into the theory… At that moment I got the happiest thought of my life in the following form: The gravitational field has a relative existence only in a manner similar to the electric field generated by magneto-electric induction. Because for an observer in free-fall from the roof of a house there is during the fall – at least in his immediate vicinity – no gravitational field. This is to say, if the observer lets go of any bodies, they remain, relative to him, in a state of rest or uniform motion…

This is similar to most modern statements of the principle, in the sense that it asserts a gravitational field – over a sufficiently small region (“immediate vicinity”) – can be “transformed away” by a suitable choice of free-falling coordinate system. Nevertheless, some modern scholars have claimed that Einstein never endorsed this “infinitesimal” form of the equivalence principle in arbitrary gravitational fields. For example, John Norton (1985) accuses Pauli of misrepresenting the principle by stating it in this form, and yet Einstein himself explicitly tells us that this is how he first conceived the idea, and how he continued to view it in 1920. Of course, in the same 1920 article he went on to say

One can also start with a space that has no gravitational field. A material point in this space, when sufficiently distant from other masses, behaves free of acceleration relative to an inertial system K. However, if one introduces a uniformly accelerated coordinate system K′ relative to K (uniformly accelerated parallel translation), … we can also view K′ as an admissible system (at rest) and attribute the acceleration of masses relative to K′ to a static gravitational field that fills the entire space that is under consideration.

This is similar to Einstein’s actual statement of the principle in the 1907 review article, and also to the formulation in his 1916 paper on the general theory, but it’s worth noting that he presents it here as a secondary alternative, another side of the same coin. That he considered both of these as entailed by the equivalence principle can be seen from his autobiographical notes, written in 1949:

Now it came to me, the fact of the equality of inertial and gravitational mass, i.e., the fact of the independence of the gravitational acceleration from the nature of the falling substance, may be expressed as follows: In a gravitational field (of small spatial extension) things behave as they do in a space free of gravitation, if one introduces into it, in place of an “inertial system”, a frame of reference accelerated relative to the former.

We also find in Einstein’s obituary for Ernst Mach (1916) a clear expression of the idea that it is not possible to distinguish – locally – a gravitational field from an accelerating coordinate system. He wrote that, although Mach clearly recognized many of the weaknesses of classical mechanics and the principle of inertia

…the vivid consciousness was missing that the equivalence of inertial and gravitational mass elicits a postulate of relativity in a wider sense, because we are not in a position to decide by experiments if the falling of a body relative to a coordinate system is caused by the presence of a gravitational field or by a state of acceleration of the coordinate system.

In some ways the clearest expression of the principle is the one given in Einstein’s 1918 paper on the foundations of the general theory, where he wrote

Inertia and gravity are phenomena identical in nature. From this and from the special theory of relativity it follows necessarily that the symmetric fundamental [metric] tensor g_μν determines the metric properties of space, the inertial behavior of bodies in this space, as well as the gravitational effects.

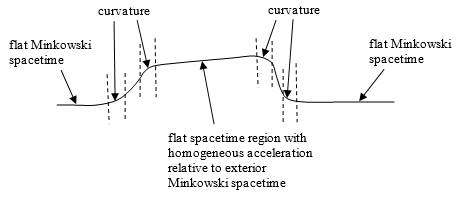
This and many other similar statements show that, unlike many modern scholars, Einstein did not regard “flat” Minkowski spacetime as being free of a gravitational field. He regarded the inertial field and the gravitational field as identical, represented by the metric tensor. In particular, he did not identify curvature with gravitation, which is why in his 1907 review article he was able to speak about a “homogeneous gravitational field”. According to some modern physicists this is a contradiction in terms, because they maintain that a gravitational field is identical with intrinsic curvature of the spacetime manifold, whereas (by definition) curvature is absent from a homogeneous gravitational field. Nevertheless, it is possible – at least in principle – to construct such a thing, by a suitable arrangement of masses – a fact which strangely doesn’t seem to embarrass those who identify gravity with curvature. Admittedly this is not a trivial proposition, as can be seen from considering the gravitational field of an infinite wall, which is perfectly homogeneous in Newtonian theory but contains subtleties in general relativity. Still, the curvature inside a massive spherical shell is zero, and yet clocks “run slow” inside the shell compared with outside clocks. This illustrates that gravity is not a local phenomenon, which is another way of expressing the equivalence principle. An even more stark example is depicted crudely in the figure below.

There are enough degrees of freedom in the placement of masses that it’s possible to produce a wide variety of fields and set the components of the curvature to zero within some region. Obviously this situation requires the existence of some curvature somewhere, and would exist only transiently, but the interior region can be intrinsically flat (similar to the interior of a spherical shell), even though free objects in the interior accelerate relative to the flat exterior spacetime. Would we really say there is no gravitational field in the “flat” interior region? This shows that it is too simplistic to identify gravity with curvature. It is analogous to claiming an absolute distinction between electric and magnetic fields. The approach advocated by Einstein – regarding the metric tensor as both the gravitational and the inertial field, regardless of whether there is curvature at any given point – is much more intelligible.

In Einstein’s 1921 Princeton lectures (published in book form as “The Meaning of Relativity” in many subsequent authorized editions up to 1955) we find another clear assertion of the infinitesimal version of the equivalence principle:

In the immediate neighborhood of an observer, falling freely in a gravitational field, there exists no gravitational field. We can therefore always regard an infinitesimally small region of the space-time continuum as Galilean.

Despite all these clear statements, Norton (1985) argues that Einstein not only didn’t endorse the “infinitesimally flat” interpretation of the equivalence principle, but actually gave a “devastating” argument against it. This refers to Einstein’s 1917 correspondence with Moritz Schlick on how (and whether) the geodesic equations of motion of general relativity can be derived from the assumption of local inertial motion together with the equivalence principle. Schlick had written an exposition (which Einstein generally admired) of relativity theory, but on this one point Einstein objected:

[Your] derivation of the law of motion of a point mass... is based on the premise that the point moves in a straight line as seen from the local coordinate system. However, from this nothing can be derived. The local coordinate system is generally significant only at the infinitesimal level, and at the infinitesimal level every continuous line is straight.

Taken out of context, Einstein’s claim that “every continuous curve is infinitesimally straight” would be rather puzzling. It's true that the difference between the tangent directions at two points on a continuous curve goes to zero as the points are brought arbitrarily close together, but the measure of deviation from straightness is not this difference, but rather this difference divided by the path distance between the two points. In other words, the deviation from straightness is represented by the rate at which the tangent direction changes per unit distance along the curve. This rate does not go to zero in the infinitesimal limit. Of course, to evaluate this rate in an unambiguous way, we need to be able to single out a suitable coordinate system at the given point. In Riemannian geometry this is represented by Riemann normal coordinates, which can be defined at any given point O to not only have vanishing Christoffel symbols at that point, but to also be such that the ratios of the coordinates of any other given point P in the vicinity of O are equal to the ratios of the differential components of the geodesic path OP at the origin, and such that the sum of the squares of the coordinates equals the square of the extremal path distance from the origin. In a flat manifold such coordinates can be extended indefinitely, but even on a curved manifold they are well-defined out to some finite distance from the given point O, with this distance being dependent on the amount of curvature. (Beyond that distance the coordinates overlaps and hence are no longer well-defined.) It can be shown that the geodesic curves of the manifold are precisely the curves that are unaccelerated in terms of the Riemann normal coordinates at every point along the curve. Hence the idea that we arrive at geodesic motion by combining Galileo’s law of inertia with the equivalence principle is basically valid.

Nevertheless, Einstein was justified in taking exception to Schlick’s derivation, because Schlick didn’t introduce Riemann normal coordinates, but rather based his argument on the assertion that Minkowski coordinates can be defined in an infinitesimal region. Moreover, he then proceeded to treat the infinitesimal line element  ds  as if it was of non-zero extent, by claiming that the “law of motion” of an inertial path is expressed by the line element

This could be construed as a valid equation for a straight line only if the differentials were replaced with finite increments and the metric was Minkowskian over a finite region. Needless to say, the terms of this “line element” are actually infinitesimals, and this relation between the differentials applies to any curve in spacetime, not just to straight or inertial paths. Thus Einstein was correct in pointing out that nothing can be inferred from this about the “law of motion” of inertial particles. When he said every curve is infinitesimally straight, he just meant that the line element (which Schlick was presenting as the equation of an inertial path) applies to all paths, whether they are inertial or not.

Having recognized the vacuity of Schlick’s argument, the question is how to repair it. We could point out the existence of Riemann normal coordinates, give the actual condition for “straightness” (i.e., the vanishing of the second derivatives) in terms of such coordinates, and then show how those conditions transform into the geodesic equations in terms of arbitrary coordinates. This would carry through, in a legitimate way, the basic idea that Schlick seemed to be trying to express, which is that “straightness” in the infinitesimal implies geodesics in the finite regime. However, this approach requires more mathematical sophistication than may have been desirable in a popular book of this kind. So, Einstein apparently tried to take a shortcut, making use of nothing but the line element, which is the only mathematical entity that Schlick had introduced (aside from a brief glimpse of the variational condition in a footnote, which is not invoked in the discussion). Einstein wrote

The correct derivation runs as follows: In principle there can exist finite (matter-free) parts of the world for which ds² = dx₁² + ... + dx₄² with an appropriate choice of the reference system. (If this were not the case, then the Galilean law of inertia and the special theory of relativity could not have held good.) In such a part of the world, the Galilean law of inertia holds with this choice of reference system; and the world line is a straight line, and therefore a geodesic, with an arbitrary choice of coordinates.

This is certainly true as far as it goes, but it doesn’t really address the issue, because it is limited to regions of flat spacetime, since it relies on the Minkowski metric being applicable over a finite region. So, to this point, Einstein has only asserted that the stationary paths are independent of coordinate system (up to diffeomorphism). Then he concludes his “correct derivation” by saying

That the worldline of a point is a geodesic in other cases too (if none other than gravitational forces act) is an hypothesis, even if a very obvious one.

Needless to say, this is not the promised “correct derivation” of the proposition that particles follow geodesic paths in curved spacetime, because he ends up claiming instead that there is no derivation, i.e., that the proposition is an independent hypothesis. This may seem surprising, in view of the fact that (as explained above) the geodesic equations of motion can be explicitly derived from the premise that the geodesic paths are precisely the paths that are linear (unaccelerated) in terms of the Riemann normal coordinates at each point. But of course that derivation relies on the hypothesis that the space is actually a Riemannian manifold, which corresponds precisely to the Equivalence Principle in general relativity. Hence, Einstein’s correction to Schlick is valid, provided we understand that the needed hypothesis to which he refers is nothing  other than the Equivalence Principle.

To substantiate this interpretation, we need only read the “corrected” version of the derivation as presented in later editions of Schlick’s book. We see immediately that his confusion was due to a basic misunderstanding of the Equivalence Principle. He actually enunciates two separate principles, one devoid of content and called by him the Equivalence Principle, and the other actually embodying the meaning of the Equivalence Principle but called by a different name. It is the latter that he invokes (with Einstein’s approval) to fulfill the required hypothesis and complete the derivation of geodesic motion.

According to Schlick, the Principle of Equivalence is the proposition that the acceleration of a free particle may, with equal justification, be interpreted as an effect of inertia or of gravity. Well, this sounds superficially somewhat like an attempt to express the Equivalence Principle, but it is too vague to carry any real meaning. The statement that acceleration can equally well be "interpreted" as the effect of either of two conventionally distinguished "causes" doesn't have much scientific content. For example, it doesn't specify what it means to "interpret" something as being an effect of inertia or an effect of gravity.  Inertia is understood to manifest itself in the lack of acceleration of a free particle, so if we say we can interpret the acceleration of a particle as an effect of inertia, we must mean something more complicated, such as the idea expressed by Einstein's elevator example. In other words, we must mean the apparent accelerated motion of a particle with reference to one system of coordinates can be interpreted as inertial (un-accelerated) motion with reference to a different (accelerated) system of coordinates. Likewise the "gravity interpretation" will have meaning only if it is expressed in terms of coordinate systems.

If Schlick had pursued this to its conclusion, he would have found (as did Einstein and most modern authors on the subject) that the real content of the Equivalence principle can be expressed by simply saying that special relativity applies in every sufficiently small region of spacetime (i.e., the very definition to which Norton objects). In fact, Schlick himself does indeed come to understand that this proposition is a crucial principle underlying general relativity. He says

…for infinitely small domains, and for systems of reference, in which the bodies under consideration possess no acceleration, the special theory of relativity holds.

Compare this with, for example, Weinberg’s statement of the Equivalence Principle

At every spacetime point in an arbitrary gravitational field it is possible to choose a locally inertial coordinate system such that, within a sufficiently small region of the point in question, the laws of nature take the same form [as in special relativity] in the absence of gravitation.

Unfortunately, instead of referring to this as the correct statement of the equivalence principle, Schlick assigns it a separate name, dubbing it the “principle of continuity”. The source of this was presumably Ernst Mach, who, along with Einstein, is usually cited as inspiring the logical positivism of Schlick and the rest of the Vienna Circle. In “The Science of Mechanics” Mach wrote

In all his reasonings, Galileo followed, to the greatest advantage of science, a principle which might appropriately be called the principle of continuity. Once we have reached a theory that applies to a particular case, we proceed gradually to modify in thought the conditions of that case, as far as it is at all possible, and endeavor in doing so to adhere throughout as closely as we can to the conception originally reached. There is no method of procedure more surely calculated to lead to that comprehension of all natural phenomena which is the simplest and also attainable with the least expenditure of mentality and feeling.

Schlick regarded the proposition that special relativity applies in infinitely small regions as an example of the principle of continuity – or rather, he regarded the thought process leading to this proposition as an example of that principle, but the proposition itself is nothing other than the equivalence principle. This is what he invokes to repair his argument about geodesic motion (in response to Einstein's criticism). He failed to recognize that this “principle of continuity” subsumes what he earlier called the principle of equivalence.  In essence, Schlick chose to bifurcate the equivalence principle into one meaningless part and one meaningful part, and call the meaningful part by a different name. Everywhere he uses the term “principle of continuity” he means what is commonly known today as the equivalence principle. Furthermore, it is the infinitesimal form of the principle, i.e., the form that Norton contends is dealt a devastating blow in the Einstein-Schlick letters. Far from supporting Norton’s claim, those letters (and the rest of the writings of Schlick and Einstein) conclusively refute it, and prove that the infinitesimal form is precisely what they had in mind, and certainly what is needed to complete the derivation of geodesic motion (given the premise of inertial motion in special relativity).

To be clear, we do not claim to be able to derive geodesic motion “from scratch”, but simply that the combination of the (naive) law of inertia for flat spacetime together with the equivalence principle (which allows us to carry over all the intrinsic properties of flat spacetime to infinitesimal regions of curved spacetime) is sufficient to imply that inertial particles follow geodesics. In view of this, Norton’s use of the Schlick-Einstein discussion to argue against the infinitesimal form of the equivalence principle is unfounded.

It’s interesting that Einstein didn’t detect Schlick’s “error” on first reading, and in fact had only praise for the treatise. He wrote to Schlick on February 6

Your exposition is of matchless clarity and perspicuity… I have absolutely nothing to criticize, but can only admire the pertinence of your way of thinking and expression.

Not until six weeks later, on March 21, did he write a follow-up note, containing the objection discussed above. He wrote:

Upon re-reading your fine essay in Naturwissenschaften I do find another small inaccuracy. I am informing you of it in case your article is reprinted elsewhere…

Schlick dutifully altered the passage in question when his essay was republished a couple of years later, paraphrasing (as best he could) Einstein’s “correction”.  In the revised version, Schlick wrote

If we could now regard the domains of the 'local' system as being infinitesimal, the whole world-line in it would shrink to an element ds, [so] the reflection made above would become meaningless, and we could draw no further inferences. However, since the Law of Inertia and the Special Theory of Relativity have been so widely confirmed by experience, it is clear that there must in reality be finite regions, for which, if we choose a suitable system of reference, [the Minkowski line element is valid], viz. those parts of the world in which, with this chosen system, no perceptible influence of gravitating matter exists. In it the world-line is for this system a straight line, and consequently for arbitrary systems a geodetic line.

Up to this point he is talking purely about flat spacetime, and repeating Einstein’s explanation about how the straight lines in terms of Minkowski coordinates generalize to geodesics in terms of arbitrary coordinates. Hence there is no physical content, it merely describes the mathematical consequences of changing the coordinate system. Then Schlick continues

We now again recall our Principle of Continuity (according to which the new laws are to be assumed, in such a way that the old laws are contained in them unchanged as nearly as possible, and the new ones resolve into the latter for the limiting case) ; and we then make the hypothesis that the relation obtained in this way is valid quite generally for every motion of a point under the influence of inertia and gravitation, i.e. that the world-line of the point is always a geodetic even when matter is present. This gives us the desired fundamental law.

As he describes it here, especially in the parenthetical comment echoing Mach, the “principle of continuity” has no specific content, but is just a methodological prescription for extending existing theories. One could argue that this “principle” is hopelessly ambiguous for extrapolating the trajectory of an existing theory into a new domain.

Nevertheless, as we saw previously, Schlick contends that, in this context, the principle of continuity warrants the proposition that “for infinitely small domains… the special theory of relativity holds” (and tacitly that spacetime can be represented by a pseudo-Riemannian manifold), which is nothing but the equivalence principle. So, in this step of his explanation, he is simply invoking the equivalence principle, albeit under a different name. Admittedly he doesn’t explicitly mention (in the main text) the actual condition of “stationarity” which allows us to extend the infinitesimal geodesics to arbitrary lengths, but he does present the variational integral in a footnote, which is perhaps sufficient for a popular account. As an aside, we note that Mach’s statement of the principle of continuity (echoed in Schlick’s parenthetical description) anticipates Bohr’s “correspondence principle”.

Torretti (1983) repeated the claim that “every curve is straight in the infinitesimal”, and to support this he notes that lines of constant latitude on the Earth’s surface are generally not geodesics, even though they may be considered (by local townspeople) to be “approximately straight” in a small region. But this is a false analogy, precisely because lines of constant latitude are not straight lines on the Earth’s surface, despite how they may be informally regarded, and the deviation from “straightness” of these lines is independent of how small a region we consider. It is perfectly possible at any point on the surface of a sphere to define – by means of local absolute measurements – a set of Riemann normal coordinates, in terms of which the geodesics through the origin are precisely the straight lines, i.e., the curves whose second derivatives vanish. Lines of constant latitude are not straight in this sense, and their non-straightness is independent of how small a region we consider. Granted there may be practical difficulties in making measurements on a very small scale, just as it may be practically unfeasible to measure the speed of a moving object over an arbitrarily short duration of time, but it does not follow that all objects are motionless.

Torretti (like Norton) confuses properties of the manifold with properties of the coordinate systems. Recall that Einstein explicitly distinguished between these two things, at least for flat manifolds, in his letter to Schlick, when he said the straight lines are the curves with zero second derivatives in terms of Minkowskian coordinates, and he then asserted that these lines are also straight even if we express them in terms of any other coordinate system, because straightness is invariant. By saying this, Einstein is stipulating that he is not defining straightness as a coordinate-dependent thing (such as one might define lines of constant latitude as “straight”). He recognizes that we can always define coordinates (even in a flat manifold) that curve in tandem with any given path, such that the curve’s second derivative is zero in terms of these coordinates, but this is of no significance, because straightness is a coordinate-independent quality, based purely and unambiguously on the metrical properties of the manifold. Lines of constant latitude on a sphere are not straight in this coordinate-independent sense, regardless of how small a region we consider, so Torretti’s argument is based on a misconception. Einstein was correct in saying that the proposition that particles move along geodesics in spacetime was a hypothesis, but he was wrong in saying that it was a separate hypothesis from the combination of the principle of inertia in flat spacetime and the equivalence principle. These two principles already entail the general geodesic hypothesis, because even in flat spacetime we can define physical straightness only in terms of the metrical properties of the manifold, and these properties are carried over, locally, to curved spacetime by the equivalence principle. Hence we must conclude that Einstein (not to mention Norton, Ohanian, and Torretti) was mistaken in thinking that a separate hypothesis is needed.

Ironically, in later years Einstein continued to be vexed by this issue, and he tried to show that the geodesic hypothesis is actually unnecessary, because it is implicit in the field equations themselves. It’s true that the field equations of general relativity entail geodesic motion for mass-energy (in the absence of non-gravitational forces) but, as explained elsewhere, this is really just a consequence of the fact that Einstein chose for his field equations a gravitational tensor whose covariant derivative vanishes identically, to ensure local conservation of energy-momentum, and this requirement is essentially equivalent to the geodesic hypothesis. Weinberg, for one, downplayed the investigations of Einstein and others into the question of whether the equations of motion in general relativity follow from the field equations (a by-product of which was the development of the post-Newtonian approximation for celestial mechanics), commenting that “the equations of motion in general relativity should be derived from the equations of motion in special relativity and the Equivalence Principle”.

Incidentally, it’s interesting that Einstein often expressed his basic principles in terms of "impossibilities", such as the impossibility of distinguishing between inertia and gravity in suitable circumstances. He apparently borrowed this approach from thermodynamics, whose first and second laws he characterized as assertions of the impossibility of perpetual motion machines of the first and second kind. Perhaps this was due to his experience as a patent examiner.

The validity of Einstein’s strong version of the equivalence principle has been (and continues to be) challenged by many authors, usually based on the claim that tidal effects and/or intrinsic curvature make it possible to distinguish gravity from acceleration, even over arbitrarily small regions of spacetime. One of the most outspoken critics was J. L. Synge, who famously wrote (in his 1960 text on general relativity)

I have never been able to understand this Principle… Does it mean that the effects of a gravitational field are indistinguishable from the effects of an observer’s acceleration? If so, it is false. In Einstein’s theory, either there is a gravitational field or there is none, according as the Riemann tensor does not or does vanish. This is an absolute property; it has nothing to do with any observer’s world-line. Spacetime is either flat or curved… The Principle of Equivalence performed the essential office of midwife at the birth of general relativity, but… I suggest that the midwife be now buried with appropriate honors and the facts of absolute space-time faced.

Clearly Synge was a proponent of the idea that gravity is to be identified with curvature, an idea which, as discussed above, is fundamentally contrary to the meaning and content of general relativity. Carrying on with this tradition, Ohanian argued that we can easily detect the presence of gravitation in a freely falling region by noticing the tidal distortion exhibited by a non-viscous drop of liquid in free fall. He observes that this distortion does not go to zero as the size of the droplet approaches zero. However, this reasoning is fallacious, because the equivalence principle is understood to refer to sufficiently small regions of spacetime, not just of space. We must consider a small spatial region in the free-falling frame over a sufficiently short duration of time. (This can also be regarded as a spatial limitation from the standpoint of the “stationary” frame.) When Ohanian's water droplet enters this region, the molecules are already configured with the tidal bulge, and when those molecules depart the region they are in the very same configuration. This is just a re-statement of Einstein’s story about the man falling from a roof, who finds that, if he lets go of some objects, they remain relatively stationary or move uniformly. This does not disprove the equivalence principle, it confirms it. The molecules of the droplet have exhibited no acceleration relative to this free-falling system of coordinates. The particular way in which those molecules were configured when they entered the region is irrelevant.

In his book “Gravitation and Spacetime”, Ohanian  describes an actual measurement technique which he claims falsifies the equivalence principle. He describes a small (a fraction of a meter) device capable of detecting extremely small amounts of tidal distortion while in free fall. However, he blithely mentions that the measurement precision is proportional to the “settling time”, which he says is roughly 10 seconds. Well, this time interval represents three billion meters, which hardly qualifies as infinitesimally small, and Ohanian admits that the detected tidal effects go to zero as the time interval goes to zero. Far from falsifying the equivalence principle, this (again) merely confirms it.

It is sometimes argued that the equivalence principle is true but trivial, because on an infinitesimal basis we can choose a coordinate system that makes any curve “straight”, but this is just a repetition of Einstein’s objection to Schlick’s derivation of geodesic motion. We cannot make any arbitrary curve “straight” in the sense of being stationary under continuous variations. Of course, as noted above, we can choose a coordinate system that is accelerated in tandem with a given particle, but if (for example) we match the acceleration of an electron in an electric field, we will find that a neutron is generally not in uniform motion with respect to those coordinates, even at the very same point. Hence the acceleration produced by an electric field cannot be “transformed away” by a change of coordinate systems. In contrast, if we choose a coordinate system to match the gravitational free fall of a particle, then every other particle has the same acceleration at that point. This is by no means a trivial fact. (Einstein called it “extremely strange” in his “Ideas and Methods” paper.)

The equivalence principle signifies that there is no gravitational force, per se. In a region of spacetime where gravity exists, there is nothing "there" other than spacetime, and the inertial motion of mass-energy. Gravitation is an attribute of spacetime, rather than something that exists within spacetime. All the other forces in nature, such as electromagnetism, seem to exist within space and time, as do all other forms of mass-energy. This is one of the fundamental reasons that gravitation doesn't fit easily into the framework of the other fundamental forces and particles. It also helps explain the approach taken by the minority of researchers (including Einstein) who treat gravitation, inertia, and spacetime as the primary objects of study, rather than following the majority who take non-gravitational forces and particles (which seem to exist within spacetime) as the main focus of interest.

By the way, Einstein had occasion to respond directly to the charge that the equivalence principle is trivial because it applies in general only over infinitesimal regions. In reply to a paper by Ernst Reichenbacher in 1920 he wrote

[Reichenbacher] raises the objection against the principle of equivalence that gravitational fields for finite spacetime domains in general cannot be transformed away. He fails to see that this is of no importance whatsoever. What is important is only that one is justified at any instant and at will (depending upon the choice of a system of reference) to explain the mechanical behavior of a material point either by gravitation or by inertia. More is not needed; to achieve the essential equivalence of inertia and gravitation it is not necessary that the mechanical behavior of two or more masses must be explainable by the mere effect of inertia by the same choice of coordinates. After all, nobody denies, for example, that the theory of special relativity does justice to the nature of uniform motion, even though it cannot transform all acceleration-free bodies together to a state of rest by one and the same choice of coordinates.

He had made the very same point in a footnote to his 1911 paper on light deflection:

Of course we cannot replace any arbitrary gravitational field by a state of motion of the system without a gravitational field, any more than, by a transformation of [special] relativity, we can transform all points of a medium in any kind of motion to rest.

Disagreements about the meaning and significance of the equivalence principle are, in a sense, extensions of the old debates about the principle of least action. Some scientists, from Maupertius to Planck, have regarded the principle of least (or stationary) action with almost mystical reverence, as some kind of expression of divine will, whereas others have seen it as merely a descriptive device, applicable in many (but not all) contexts, with no profound underlying significance. (The “sum over all paths” formulation, advanced by Feynman, goes some way towards “explaining” why stationary action is so prevalent, but only by means of quantum superposition, which then leads to the measurement problem of quantum mechanics.) It’s interesting that the non-local and even teleological aspects of general relativity were already present in the ancient debates over least action, and the same concerns can be seen in Einstein’s “correction” of Schlick. The claim that “every continuous path is infinitesimally straight”, and therefore it is not possible to distinguish straight paths from curved paths on an infinitesimal basis, is essentially equivalent to the claim that “infinitesimal stationarity” cannot be the cause of anything. In other words, if we claim that over a sufficiently small interval the difference between the motion of a particle moving on a curved path cannot be physically distinguished from a particle moving on a straight path, then we cannot account for the fact that the particle moves in a straight path (even in flat spacetime) – unless we invoke the principle of least action over a finite interval.

Hence we are led to a non-local application of the principle if we insist that it can have no causative effect over infinitesimal intervals. Indeed the sum-over-all paths explanation is explicitly non-local, which of course is what leads to the measurement problem. An alternative approach is to simply reject any sort of causal implications, and regard geodesic motion (stationary action) as purely descriptive, or else to suggest that it is tautological for free objects to move along geodesics because we ultimately define geodesics (and the rest of our spatio-temporal model) by the paths of free objects. The question then becomes one of consistency, i.e., why there so much coherence in the motions of objects, such that it is possible to define a single system of space and time coordinates (not necessarily flat) in terms of which the motions of such a large number of entities are (at least approximately) geodesics.

Return to Math Pages Main Menu