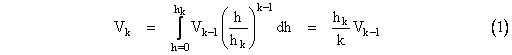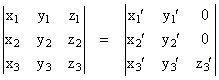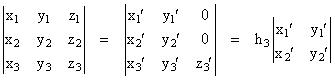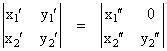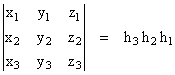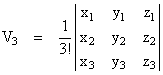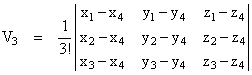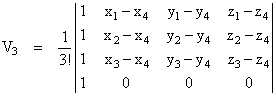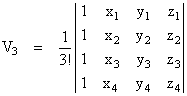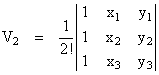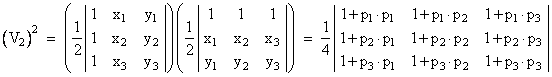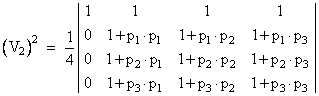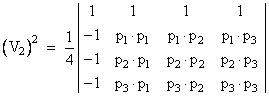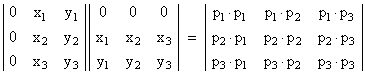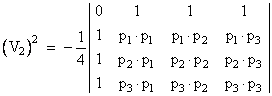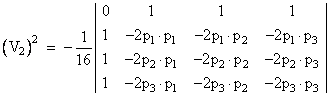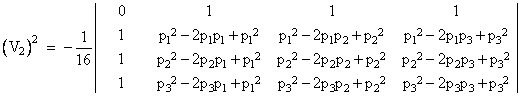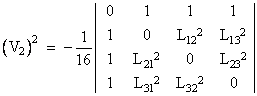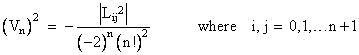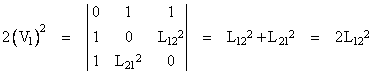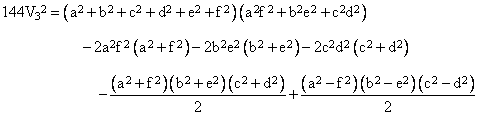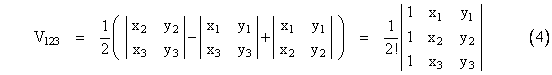|
Simplex Volumes and the Cayley-Menger Determinant |
|
|
|
A simplex in n-dimensional Euclidean space is a convex solid with n+1 vertices. Thus in one-dimensional space a simplex is just the line segment between two specified points. A simplex in two-dimensional space is a triangle three vertices), a simplex in three-dimensional space is a tetrahedron (four vertices), and so on. The content of a simplex (viz, the length of a one-dimensional simplex, the area of a two-dimensional simplex, the volume of a three-dimensional simplex, and so on) can be expressed very simply as a function of the coordinates of the n+1 vertices. First, note that any vertex of a simplex in k-dimensional space can be regarded as the apex of a “pyramid” on a (k-1)-dimensional base defined by the other vertices. Letting Vk-1 denote the content of the base, and h the perpendicular distance of the apex from the sub-space containing the base, the content Vk of the pyramid is given by |
|
|
|
|
|
|
|
Therefore, applying this formula to the vertices (in any order) recursively, beginning with k = n, we have |
|
|
|
|
|
|
|
where h1 is simply the distance between the first two vertices, h2 is the height of the third vertex above the line containing those two vertices, h3 is the height of the fourth vertex above the plane containing the first three vertices, and so on. Thus the content of a n-dimensional simplex is 1/n! times the “heights” of the vertices (taken in any linear sequence) above the sub-space containing the previous vertices. |
|
|
|
Now, to determine the required “heights”, we begin by noting that, without affecting the content, the entire arrangement of vertices can be rigidly translated in space so that one vertex is located at the origin. We can then construct an n x n matrix consisting of the n coordinates of each of the remaining n vertices. For example, with n = 3 we construct the matrix |
|
|
|
|
|
|
|
where (xi,yi,zi) with i = 1,2,3 are the coordinates of three vertices, remembering that the fourth vertex is located at the origin. Any rigid rotation of these points about the origin will leave the determinant of this matrix unchanged (because the determinant of a rotation matrix is 1 by definition). In general we can apply an n-dimensional rotation that places n-1 of the vertices into a sub-space orthogonal to one of the axes. Thus in our example we can rotate the configuration so that the first two vertices are in the xy plane, resulting in a transformed matrix with the same determinant but with zeros in all but the last element of the last row, so we have |
|
|
|
|
|
|
|
Here the z3’ coordinate is the height of the third vertex above the subspace containing the other three vertices (including the origin). By co-factor decomposition of the last column, and letting h3 denote z3’, this determinant can be written as |
|
|
|
|
|
|
|
The 2 x 2 matrix in the right hand expression contains the coordinates of two of the vertices of a two-dimensional simplex in the xy plane (remembering that the third vertex is at the origin). Without affecting the value of this determinant, we can apply a rotation that places the first vertex on the x axis, so we have |
|
|
|
|
|
|
|
Here the y2” coordinate is the height of the second vertex above the subspace (i.e., the line) containing the other two vertices (including the origin). By co-factor decomposition of the last column, and letting h2 denote y2”, this determinant can be written as h2 x1”. Noting that x1” is the height h1 of the first vertex over the origin, we have |
|
|
|
|
|
|
|
Substituting into equation (2), we find that the content of the original three-dimensional simplex with one vertex at the origin is given in terms of the coordinates of the other three vertices by |
|
|
|
|
|
|
|
This derivation immediately generalizes to simplexes in any number of dimensions. Also, we can immediately write the volume of an n-dimensional simplex with (n+1) arbitrary vertices, without requiring one of them to be at the origin. In our three-dimensional example we can imagine four arbitrary vertices, including a fourth at (x4,y4,z4), and we can write the content of this simplex as |
|
|
|
|
|
|
|
Furthermore, we know by co-factor decomposition that we can write this as the determinant of an n+2 dimensional matrix |
|
|
|
|
|
|
|
Now we can make use of the fact that adding a multiple of any column (or row) to another column (or row) doesn’t change the determinant. To see why this is so, note that if any column vector ci is replaced with ci + kcj where cj is one of the other column vectors, then each co-factor is multiplied by an element of ci + kcj, and hence it’s clear that the determinant is the sum of the original determinant plus the determinant of the original matrix with ci replaced by kcj. But the latter determinant is identically zero, because one column is a multiple of another. So, applying this proposition to the above matrix, we can add x4 times the first column to the second column, and so on, to give |
|
|
|
|
|
|
|
This derivation is completely general, and applies to simplexes in n dimensions, enabling us to compute the content in terms of the coefficients of the (n+1) vertices. |
|
|
|
However, it is sometimes of interest to express the volume of a simplex in terms of the edge lengths rather than the vertex coordinates. To illustrate how we can derive such an expression, consider a two-dimensional simplex with vertices pi = (xi,yi), i = 1,2,3. We know the content is given by the determinant |
|
|
|
|
|
|
|
Since a matrix and its transpose have the same determinant, we also have |
|
|
|
|
|
|
|
where pi ∙ pj = xixj + yiyj. We can express this as the determinant of a matrix of dimension increased by one, as follows. |
|
|
|
|
|
|
|
To see that this equals the previous determinant, simply note that the first element in the first column is 1 and its co-factor is the previous matrix. All the other elements in the first column are zero, so the overall determinant is equal to the previous determinant. |
|
|
|
Now we again make use of the fact that the determinant of a matrix is unchanged if any multiple of a row is added to any other row. Thus we can subtract the first row from each of the other rows to give |
|
|
|
|
|
|
|
Notice that the determinant of the co-factor of the upper left element is zero, as can be seen from the fact that |
|
|
|
|
|
|
|
The determinants on the left are obviously zero, so the right side is also zero. Hence the upper-left element of the prior matrix has no effect on the value of the determinant, so we can set it to zero. Also, making use of the fact that multiplying the elements of any column (or row) by a constant has the effect of multiplying the determinant by that constant, we can negate the first column to give |
|
|
|
|
|
|
|
If we now multiply each of the last three columns by -2, and then multiply the first row by -1/2, this expression becomes |
|
|
|
|
|
|
|
Now, for i = 1 to 3, we add the first column multiplied by pi ∙ pi to the (i+1)th column, and we add the first row multiplied by pi ∙ pi to the (i+1)th row, to give the expression |
|
|
|
|
|
|
|
where all the products of the pi are understood to be dot products. Noting that the square of the distance between pi and pj is |
|
|
|
|
|
|
|
we have the expression, called the Cayley-Menger determinant, for the area of a triangle in terms of the edge lengths |
|
|
|
|
|
|
|
Writing this out in full, and letting a,b,c denote the three edge lengths, this gives |
|
|
|
|
|
|
|
which of course is Heron’s formula for the area of a triangle. The derivation is completely general, giving the content of a simplex in n dimensional space for any n, with the understanding that the leading coefficient is the square of the factor 1/n! (from the determinant expression based on equation (2)), multiplied by -1 to compensate for the sign reversal of the first column, and by 1/(-2)n+1 to compensate for the n+1 column multiplications, and by 1/(-1/2) to compensate for the row multiplication. Therefore, if we define fictitious lengths L00 = 0 and L0j = Lj0 = 1 for j = 1 to n+1, the Cayley-Menger determinant giving the squared content of an n-dimensional simplex can be written succinctly as |
|
|
|
|
|
|
|
Thus the squared content of a one-dimensional simplex (i.e., a line segment between two vertices) can trivially be expressed in terms of the edge length as |
|
|
|
|
|
|
|
Likewise the volume of a tetrahedron is given in terms of the edge lengths by |
|
|
|
|
|
|
|
Letting a,b,c,d,e,f denote the lengths L12, L13, L14, L23, L24, L34 respectively, this formula gives |
|
|
|
|
|
|
|
which is equivalent to the formula found in the 15th century by Piero della Francesca, except that he transposed the edges a and f and negated the sign of the last term. As one would expect, the first terms of this formula are symmetrical, and the last term is anti-symmetrical, in the pairs (a,f), (b,e), and (c,d), which correspond to the side pairs (L12, L34), (L13, L24), and (L14, L23), which represent the pairs of opposite edges. (It’s interesting to compare this expression for the squared volume of a tetrahedron with the one based on the vector triple product – and its square – in the note on a “quarky formula”.) |
|
|
|
In two dimensions the equation for the content of a simplex is completely symmetrical in the three edge lengths, so there is a unique content for any multi-set of edge lengths. However, as discussed in the note on Piero della Francesca’s formula, the equation for the content of a four-dimensional simplex is not fully symmetrical, so it can give up to 30 distinct arrangements (and therefore contents) for a given multi-set of edge lengths. |
|
|
|
Incidentally, we can think about the transition from central simplexes to arbitrarily-positioned simplexes in two different ways. To illustrate, recall that the signed area of a triangular region of the plane with one vertex at the origin and the other two vertices at (x1,y1) and (x2,y2) is |
|
|
|
|
|
|
|
In the preceding discussion we generalized this to triangles with three arbitrary vertices p1 = (x1,y1), p2 = (x2,x1), and p3 = (x3,y3), by simply noting that we can subtract the coordinates of p3 from each of the points, thereby effectively shifting p3 to the origin, and write the area using the central formula |
|
|
|
|
|
|
|
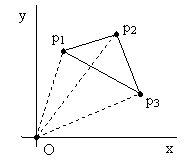
A different (but equivalent) conceptual approach is to evaluate the areas of the three central triangles formed by combining the origin with any two of the given vertices, as shown in the figure below. |
|
|
|
|
|
|
|
We can express the area of triangle p1p2p3 as the sum of the areas of the central triangles Op1p2 and Op2p3 minus the area of the central triangle Op1p3. Thus we can write |
|
|
|
|
|
|
|
where again we’ve used of the fact that the determinant of a matrix is the sum of the elements, with alternating signs, of a single column multiplied by their respective co-factors. We’ve already shown algebraically that the determinants on the right hand side of equations (3) and (4) are equivalent, so this is a legitimate conceptual approach, although the previous approach is simpler, since it avoids the need to verify the signs of the co-factor terms. |
|
|