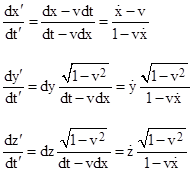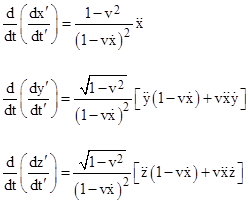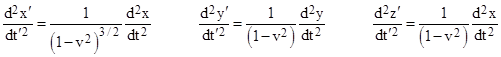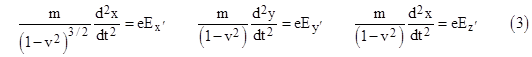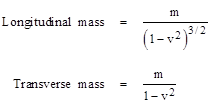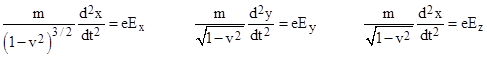|
Transverse Mass in Einstein’s Electrodynamics |
|
|
|
Some controversy exists on the subject of Einstein’s expression for the “transverse mass” of a particle in his 1905 paper on the electrodynamics of moving bodies. The expression in question appears in Section 10 of the paper, where Einstein notes that if a particle (which he calls an “electron”) of mass m with electric charge e is initially at rest at a location where the components of the electric field are Ex, Ey, and Ez, then by definition the “force” on the particle has the components eEx, eEy, and eEz, and the subsequent motion of the particle during the first incremental period of time is given by the equations |
|
|
|
|
|
|
|
where x,y,z,t are inertial coordinates in terms of which the particle is initially at rest. Now consider the same charged particle at the same location but moving in the positive x direction with speed v. The particle is now momentarily at rest with respect to a system of inertial coordinates x′,y′,z′,t′, in terms of which the components of the electric field are |
|
|
|
|
|
|
|
where Bz and By are the components of the magnetic field (at the location of the particle) in terms of the original coordinates. (See the note on Force Laws and Maxwell’s Equations for the derivation of these expressions.) Now, in accord with the principle of relativity, the components of the force on this particle in terms of the momentarily co-moving x′,y′,z′,t′ coordinates are eEx′, eEy′, and eEz′., and the motion of the particle during the first incremental period of time is given in terms of these coordinates by equations of the same form as (1), which is to say |
|
|
|
|
|
|
|
The objective is to transform these equations of motion back into the original (unprimed) coordinates x,y,z,t to give the equations of motion of a moving particle. In units such that c = 1, the two systems of coordinates are related by the Lorentz transformation |
|
|
|
|
|
|
|
and we also know that the particle initially has dx/dt = v and dy/dt = dz/dt = 0. The transformation equations give the total differentials |
|
|
|
|
|
|
|
from which we get the ratios |
|
|
|
|
|
|
|
where dots denote derivatives with respect to t. Differentiating again with respect to t gives |
|
|
|
|
|
|
|
We also have |
|
|
|
|
|
so we can divide through the previous three equations by this expression, and then insert the values dx/dt = v and dy/dt = dz/dt = 0 to give the results |
|
|
|
|
|
|
|
Substituting into equations (2), this gives |
|
|
|
|
|
|
|
All this is perfectly straightforward and unobjectionable. Notice that the right hand sides of these equations are the components of the force on the particle in terms of the co-moving coordinates x′,y′,z′,t′, and the second derivative on the left hand sides are in terms of the original (un-primed) coordinates x,y,z,t, so these equations are “mixed”, i.e., they involve quantities defined in terms of different systems of coordinates. In his 1905 paper, Einstein says (correctly) that the right hand sides |
|
|
|
…are the components of the ponderomotive force acting upon the electron, and are so indeed as viewed in a system moving at the moment with the electron, with the same velocity as the electron. (This force might be measured, for example, by a spring balance at rest in the last-mentioned system). |
|
|
|
Thus he clearly and correctly identified the expressions eEx′, etc., as the forces in terms of the co-moving system of coordinates. He is right to specify this, because we know that forces are not invariant under Lorentz transformations, so we cannot talk unambiguously about the force; we must specify the system of reference. At this point, referring to “the ordinary point of view”, Einstein remarks that |
|
|
|
If we call this force simply “the force acting upon the electron”, and maintain the equation mass x acceleration = force, and if we also decide that the accelerations are to be measured in the stationary system, we derive from the above equations |
|
|
|
|
|
|
|
These expressions come directly from the left hand sides of the previous equations, with the longitudinal mass corresponding to the equation of motion in the x direction, and the transverse mass corresponding to the equations of motion in the y and z directions. The equation for the “transverse mass” has led many authors to criticize Einstein, intimating that he “erred” (expecting the denominator to be raised to the 1/2 power), but this is based on a misunderstanding. All the above statements are perfectly accurate and correct, since Einstein has explicitly stated that these are the expressions for longitudinal and transverse mass given the three stipulations (1) we define “mass” as the “force” divided by the “acceleration” in the instant when it is beginning to accelerate from rest with respect to the momentarily co-moving coordinates, (2) we use the force on the particle as would be measured in the momentarily co-moving coordinates of the particle, and (3) we use the acceleration expressed in terms of the “stationary” coordinates. Of course, there is a large amount of arbitrariness in these definitions, because (for example) we could just as well use the force components expressed in terms of the “stationary” coordinates, in which case the denominator of the expression for transverse mass would be (1−v2)1/2, as explained below. We could also define the acceleration in terms of the co-moving coordinates and arrive at different expressions. Indeed this is precisely what Einstein says |
|
|
|
With a different definition of force and acceleration we should naturally obtain other values for the masses. This shows us that in comparing different theories of the motion of the electron we must proceed very cautiously. |
|
|
|
In view of this, it’s difficult to support the idea that Einstein was mistaken or confused on the subject. He clearly pointed out the arbitrariness in the “ordinary view” of relativistic mass. The confusion and lack of clarity seems to be more on the part of subsequent critics, who think the issue relates to the definition of force rather than mass. Part of the confusion may have resulted from a footnote that was added when the paper was re-printed in 1913. The note is attributed to Sommerfeld, and it’s unknown if Einstein approved it. In any case, following the words “If we call this force simply ‘the force acting upon the electron’ ”, Sommerfeld’s note says |
|
|
|
The definition of force here given is not advantageous, as was first shown by M. Planck. It is more to the point to define force in such a way that the laws of momentum and energy assume the simplest form. |
|
|
|
This note is a non-sequitur, because Einstein’s words don’t constitute a definition of force. He was merely specifying the system of coordinates relative to which the force was to be evaluated, which is necessary because (as already mentioned) force is not an invariant quantity. No one disputes that the force to which Einstein referred, given by the quantities eEx′, etc., represents the physical force that would be measured by a co-moving spring balance (for example). Now, it so happens that the force component in the direction of motion is the same with respect to both systems of coordinates, but the transverse components are not. The well-known transformation for forces is |
|
|
|
|
|
|
|
as discussed in the note on Force Laws and Maxwell’s Equations. Therefore, if we re-write equations (3) in terms of the force components eEx, etc, which represent the physical force as measured with respect to the stationary coordinates, we get |
|
|
|
|
|
|
|
Here the components of both the force and the acceleration are expressed in terms of the same (stationary) system of coordinates. Adhering to the “ordinary” terminology mass x acceleration = force, we have the same longitudinal mass as before, but now the transverse mass is |
|
|
|
|
|
|
|
The reason this expression differs from the previous one has nothing to do with a more “advantageous” definition of force such that the laws of energy and momentum assume their simplest form. Both expressions use the same definition of force. The difference is only that the first one used the force in terms of the co-moving coordinates, whereas the second one uses the force in terms of the stationary coordinates. Neither of these has more right than the other to be called the true force, just as neither system of coordinates has the right to be called the true coordinates. Both sets of equations express exactly the same physical phenomena, provided we take care to recognize the coordinates in terms of which each variable is defined. The assignment of a name such as “transverse mass” to some particular quantity is arbitrary (as Einstein pointed out), and has no effect on the physical content of the equations. |
|
|
|
Of course, one can argue that if we’re going to define a term such as “transverse mass” we should do it in the context of an equation that expresses both the acceleration and the force in terms of the same coordinates, rather than using the acceleration expressed in terms of one system of coordinates and the force expressed in terms of another. (This ambiguity doesn’t arise in Newtonian mechanics, where both force and acceleration are invariant under transformations from one inertial coordinate system to another, whereas in special relativity these quantities are coordinate-dependent.) This is a valid reason for preferring to give the name “transverse mass” to the second expression rather than the first, but it has nothing to do with the issue that Sommerfeld raised in his footnote, which is the same issue that most authors have tried to somehow link to Einstein’s unusual expression for transverse mass. If the definition of force were really the issue, the footnote should have been attached to the subsequent clause in Einstein’s paper, in which he talks about maintaining the equation “mass x acceleration = force”. This is the point that Planck addressed in 1906, when he argued that it is more advantageous to define force not as m(dv/dt) but rather as d(mv)/dt, since we are allowing m to vary. But this is not a legitimate critique of Einstein’s argument, because Einstein explicitly applies the formulation f = ma only to the nascent acceleration from rest relative to momentarily co-moving coordinates, and in this context the quantity m represents the rest mass, which is the constant of proportionality between f and a at the initial instant of acceleration. This is why he explicitly and carefully wrote “If at a certain instant of time the electron is at rest, then in the next instant of time the electron’s motion is described by [f = ma]”. At every point along the path of an accelerating particle we can construct momentarily co-moving system of inertial coordinates, in terms of which the equation of motion f = ma momentarily applies, and we can then transform to any other relatively moving system of coordinates, thereby yielding a complete electrodynamics of moving bodies. |
|
|
|
Interestingly, Einstein skillfully exploited the very same kind of reasoning about nascent acceleration relative to momentarily co-moving inertial coordinates in his next paper on the inertia of energy, and there too essentially the same misguided criticism has been raised. (See the note Einstein on the Inertia of Energy.) It’s true that Planck (and later Tolman and Lewis) introduced some very useful conventions and definitions involving relativistic mechanics, and those conventions (as Sommerfeld said) make the laws of momentum and energy assume the simplest form for arbitrary motions. However, those innovations don’t invalidate the clear and careful reasoning on the subject in Einstein’s 1905 papers, and in fact they are entirely equivalent to the formulas that Einstein gave. |
|
|