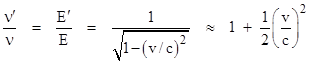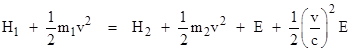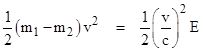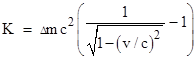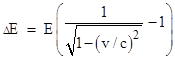|
Einstein on the Inertia of Energy |
|
|
|
Although the complete convertibility between mass and (massless) energy is not a direct logical consequence of special relativity, it is undeniable that special relativity is highly suggestive of a fundamental equivalence between mass and energy, one that is not apparent in the pre-relativistic context. In fact, this equivalence is often regarded as the most important theoretical consequence of special relativity. Ironically, the first argument given by Einstein in support of this fundamental equivalence, in a short paper published at the end of 1905, has been criticized as a petitio principii, i.e., as being based on the assumption of the thing to be proven. This charge has been debated in academic circles, but it is completely unfounded, based on misunderstanding of how the argument actually works. |
|
|
|
The argument put forward by Einstein took as its starting point the transverse Doppler effect, which in turn relies on relativistic aberration, both derived in section 7 of his previous paper on the electrodynamics of moving bodies. Furthermore, in section 8 he had shown that if a “light complex” of frequency ν and energy E is emitted from a resting body, then in terms of a coordinate system moving with speed v transversely (in terms of the rest frame coordinates) to the direction of the emitted light, both the frequency ν′ and the energy E′ of the pulse are greater than the corresponding values in the rest frame of the emitting body. Specifically, for this special purely transverse condition, we have |
|
|
|
|
|
|
|
This “transverse” shift is a uniquely relativistic effect, one that even Whittaker (a proponent of the view that Lorentz and Poincare actually discovered relativity) credits to Einstein, and it immediately leads to a very important consideration. |
|
|
|
First, we should note that the total energy E of a body consists of two parts, intrinsic and extrinsic. The intrinsic part of a body’s energy arises from internal degrees of freedom, and does not depend on the speed of motion of the overall object, whereas the extrinsic part of a body’s energy is the part that does depend on the overall motion of the body. Both parts are proportional to the quantity of mass in a given state (i.e., a specific intrinsic state and a given state of motion). |
|
|
|
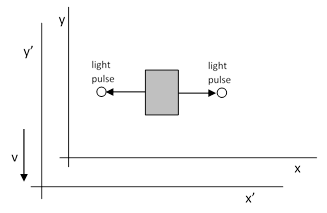
Suppose an object at rest emits two pulses of light in opposite directions. After these emissions the object is still at rest (by symmetry), so it still has no extrinsic energy, but it’s internal energy has been diminished by the amount of energy of the two pulses. Now consider the same situation in terms of a system of inertial coordinates moving with arbitrarily small speed –v in a direction transverse to the directions of the light pulses. These two cases are illustrated in the figure below. |
|
|
|
|
|
|
|
Since, by definition, the internal energy of the object doesn’t depend on the speed of the object, it is the same regardless of which system of reference we use. Letting H1 and H2 denote the internal energy of the object before and after the light emissions, and letting E denote the combined energy of those emissions, the total energy of the system in terms of the resting coordinates is |
|
|
|
|
|
|
|
In terms of the moving coordinates we still require conservation of energy, so we can equate the total energy before and after the emissions, which gives (up to second order) |
|
|
|
|
|
|
|
where we have used the classical approximation mv2/2 for the kinetic energy, and we have subscripted the mass before and after the emissions, to allow for the possibility that the inertial mass of the object may change due to the emission of energy. The crucial last term on the right hand side is the contribution of the transverse Doppler effect noted above. Subtracting the first equation from the second, we get |
|
|
|
|
|
|
|
which can be solved for E to give |
|
|
|
|
|
|
|
This signifies that the inertial mass of the object is reduced by E/c2 when it emits light pulses with combined energy E. |
|
|
|
This is clearly not a petitio principii. Einstein’s argument was criticized by Planck for its reliance on the Newtonian approximation mv2/2 for kinetic energy for a body of mass m and velocity v. However, the value of v in Einstein’s argument can be as small as we like, and surely the kinetic energy equals the Newtonian expression in the limit as v goes to zero, so its use is fairly unobjectionable. Furthermore, the use of the Newtonian approximation is not essential to the argument. In section 10 of Einstein’s paper on the electrodynamics of moving bodies he had already deduced that the kinetic energy of a particle of mass Δm moving with speed v is |
|
|
|
|
|
|
|
and the exact expression for the difference between the combined energy of the two electromagnetic pulses in terms of the stationary and the moving frames is |
|
|
|
|
|
|
|
Equating these two, as before, gives the exact relation E = Δmc2. Thus Einstein’s 1905 argument shows that the inertia of energy is a direct consequence of the transverse Doppler shift, which is a uniquely relativistic effect. Even those who downplay Einstein’s contribution to relativity acknowledge that the relativistic Doppler formula in his paper on electrodynamics was new. Since the unique transverse feature of that formula (a consequence of relativistic aberration and time dilation) determines the relation between inertia and energy in Einstein’s second paper, it is hard to support the claim that his argument is a petitio principii. Admittedly in later years (beginning already in 1906) he published several additional derivations, as did others (including Planck, Lorentz, Sommerfeld, Tolman and Lewis), but none of these represented refutations of earlier arguments. They were all attempts to further broaden and generalize the equivalence. Einstein’s original 1905 argument was actually quite powerful, since it applied to any radiant energy, so presumably it accounted for the convertibility of all the mass of an object until the object reached a temperature of absolute zero, and was in the lowest possible energy state (whatever that might be), with no further capacity to radiate energy to any surroundings. |
|
|
|
Another possible objection is to Einstein’s equating of the energy ratio E′/E with the frequency ratio ν′/ν. As Einstein remarked in his previous paper on electrodynamics “It is remarkable that the energy and the frequency of a light complex vary with the observer’s state of motion according to the same law”. He presumably had in mind the fundamental quantum relation E = hν, which he himself had just proposed in another paper, but apparently he preferred not to rely on that relation as the basis for establishing the inertia of energy. So, he derived the energy ratio based on the volume of a transformed ellipsoid multiplied by the squared amplitude of the transformed electric field. Einstein admits that this was based on Maxwell’s expression for electromagnetic energy, but the use of Maxwell’s equations does not render the derivation otiose. It’s true that those equations already imply the relation E = pc, where E is the energy and p is the momentum of an electromagnetic wave, and hence if we insert the classical definition of momentum p = mc we get E = mc2 (as had already been noted previously by others, such as Poincare and Thompson), but this doesn’t really establish any connection between radiant energy and mechanical inertia. It is merely an analogy. |
|
|
|
One might also challenge the premise that the internal energy of a body is independent of its state of motion. If, instead, we were to postulate that mass (for example) is independent of the state of motion, then the same argument would force us to conclude that the internal energy of a body varies with motion. However, the invariance of internal energy with motion is not really a postulate, it is a definition. We are certainly free to say the total energy of an object consists of two parts, one of which varies with motion and the other of which does not. This then returns us to consideration of the part that does vary with motion, and the assumption that it has the form mv2/2 in the limit as v goes to zero. This form follows directly from the definition of inertial mass as the resistance to acceleration, and the idea that work equals force times distance. Hence the objection is not valid. |
|
|
|
How, then, did the idea arise that Einstein’s 1905 derivation of mass-energy equivalence was a petitio principii? I suspect it may have originated with the American engineer and inventor Herbert Ives who, beginning around 1937, published a series of articles in “The Journal of the Optical Society of America”, declaring the Einstein’s special relativity was “not only ununderstandable, but contradicted by the facts”. Ironically, one of Ives’ experiments (performed with G. R. Stilwell) designed to discredit special relativity actually furnished the first direct measurement of time dilation, so it represented one of the strongest early confirmations of special relativity. Despite this, Ives denied the intelligibility of Einstein’s theory, and advocated a return to a Lorentzian interpretation, according to which one particular system of inertial coordinates is deemed to be “true”, and all the others merely apparent. Unfortunately, Ives’ view was limited to optics, so he never understood the mechanical origins of the concept of an inertial coordinate system, and hence he could not grasp the physical content of the Lorentz transformations. He also succumbed to the popular misconception that special relativity consists of the phrase “everything is relative”, an admittedly fatuous notion, to which he valiantly objected, but which bears no resemblance to the actual content of special relativity. In 1952 (a year before his death), he published an article entitled “Derivation of the Mass-Energy Relation”, whose abstract informs us that |
|
|
|
The reasoning in Einstein's 1905 derivation, questioned by Planck, is defective. [Einstein] did not derive the mass-energy relation. |
|
|
|
The reasoning that Ives presents in support of this assertion is patently specious. He uses the notation from Einstein’s 1905 paper, in which H is the total energy, E is the internal (rest) energy, K is the kinetic energy, L is the total energy of the emitted radiation, and the subscripts 0 and 1 signify respectively “before” and “after” the emission. In these terms, Ives concedes that Einstein has established the relation |
|
|
|
|
|
|
|
and he concedes that the celebrated result L = (m–m′)c2 follows from this if |
|
|
|
|
|
|
|
However, he argues that Einstein has merely assumed this, and hence Einstein merely assumed that which he supposedly was trying to derive. Ives concluded with the words |
|
|
|
This is the very relation the derivation was supposed to yield. It emerges from Einstein's manipulation of observations by two observers because it has been slipped in by the assumption which Planck questioned. The relation E= mMc2 was not derived by Einstein. |
|
|
|
These two sentences are wrong in several different ways. First, equation (1) was not “slipped in by assumption”, as Ives knows full well, because he previously quoted the very passage in which Einstein justified this relation. The relevant passage is |
|
|
|
Both differences of the form H – E occurring in this expression have simple physical meanings. H and E are the energy values of the same body, related to two coordinate systems in relative motion, the body being at rest in one of the systems (system (x, y, z)). Hence it is clear that the difference H – E can differ from the body's kinetic energy K with respect to the other system (system (ξ,η,ζ)) only by an additive constant C, which depends on the choice of the arbitrary additive constants in the energies H and E. We can therefore set H0 – E0 = K0 + C and H1 – E1 = K1 + C since C does not change during the emission of light. |
|
|
|
Since the constant C is arbitrary, Einstein’s assertion is simply H = E + K, which is to say, the total energy equals the internal (rest) energy plus the kinetic energy, up to an arbitrary additive constant. Furthermore, for consistency of the energy scales, the constant must not change during the emission of the light. Hence we have (1), which, combined with the previous expression, implies the mass-energy relation. Ives’ objection is entirely fatuous, despite his attempt to attribute it to Planck. He says in regard to the preceding quote |
|
|
|
Now it is by no means "clear that, etc." Thus we find Planck in 1907, after deriving the relation in question, as already described, making the following comment :"Einstein has already drawn essentially the same conclusion by the application of the relativity principle to a special radiation process, however under the assumption permissible only as a first approximation, that the total energy of a body is composed additively of its kinetic energy and its energy referred to a system with which it is at rest." |
|
|
|
Hence the justification of equation (1), described by Einstein as “clear”, was not clear to Ives, so Ives concluded that it had no justification, and that Einstein had merely smuggled it in. To support his view, Ives quoted Planck, who had (correctly) pointed out with regard to Einstein’s derivation that it assumed the simple additivity of the kinetic energy and the rest energy. This amounts to saying that Einstein used the Newtonian approximation mv2/2 for the kinetic energy, neglecting all higher order terms, which is true. But we’ve already seen that the derivation achieves its objective with an arbitrarily small value of v, and furthermore that it’s trivial to replace the Newtonian expression with the full relativistic expression without affecting the result. Ives was obviously confusing the relativistic effect of “increasing mass as a function of velocity” with the relativistic reduction in the rest mass of an object when it emits some radiant energy. The latter effect is the subject of Einstein’s derivation, whereas the former effect can (in principle) be made arbitrarily small without affecting this result. Planck’s comment in no way impugned the validity of Einstein’s derivation, but simply pointed out how one approximation could be eliminated from the derivation. Planck certainly never implied that Einstein’s equation (1) was unjustified. |
|
|
|
One further comment on Ives’ article: He referred to the relation E = mMc2, where the subscript M signifies mass. Earlier in the paper he discussed the relation E = mRc2, where the subscript R signifies radiant. According to Ives |
|
|
|
The equation relating mass to energy, E = mc2, appears in two guises. In one guise it applies to radiation existing in space, and is applicable to the interaction of this radiation in pressure and impact phenomena where the radiation retains its identity as such. In these phenomena the "m" in the relation E = mc2 is the mass equivalent of free radiation. In the second guise the relation E = mc2 applies to radiation as emitted or absorbed by matter; in this case the "m" is the mass of matter, and the significance of the equation is that it describes the gain or loss of mass by matter when absorbing or emitting radiation. If we designate the two masses as mR and mM we then have two relations E = mRc2 and E = mMc2 to be established. |
|
|
|
He doesn’t seem to have even been acquainted with the fundamental relation |
|
|
|
|
|
|
|
and how this encompasses both the energy and the momentum of any kind of entity, both matter and radiation (the latter having zero rest mass). It’s no wonder he was so confused. As discussed in The Inertia of Energy, this formula is nothing but a scaled version of the invariant spacetime interval |
|
|
|
None of this is to suggest that Einstein was fully satisfied with his 1905 derivation, which was after all just a heuristic argument for a tremendously profound principle. In 1906 he published another argument in support of the proposition that a body’s inertia depends on its energy content. This argument was based on a consideration of the center of mass of a rigid hollow cylinder, with an electromagnetic pulse emitted at one end and absorbed at the other, as illustrated below. |
|
|
|
|
|
|
|
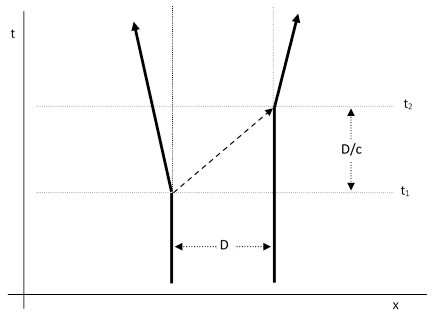
This is an ingenious argument, although it is rendered somewhat problematic by the use of a “rigid body”, with forces acting at different times on each end. A simpler form of the argument, and one that avoids the reliance on rigid bodies, is to consider two particles, each of mass m, initially at rest (in some inertial frame) and separated by a distance D. The first particle emits a directed pulse of light at time t1 which arrives at the second particle at time t2 after an elapsed time of D/c, as indicated in the space-time diagram below. |
|
|
|
|
|
|
|
From Maxwell’s equations, and more fundamentally from the invariant space-time interval, we know that the energy E and momentum p of a massless particle (e.g., a photon) are related by pc = E. Also, the center of mass at time t2 is the same as at time t1, because otherwise two particles interacting only with each other could accelerate their mutual center of mass. The momentum of the left-hand particle after the emission is (m–Δm)v, where Δm is the mass lost by the particle during emission, and v is the particle’s speed (in the leftward direction). The leftward momentum of the particle equals the rightward momentum of the light pulse, so we have E/c = (m–Δm)v. The right hand particle at time t2 is still at a distance D/2 from the center of mass, whereas the left hand particle is at a distance D/2 + (D/c)v, so it follows that |
|
|
|
|
|
|
|
Solving for the momentum p gives p = Δmc, and substituting E/c for the momentum, we get (again) the result E = Δmc2. |
|
|
|
This derivation is sometimes presented as the entirety of Einstein’s argument in the 1906 paper, but if this were so, it would be a somewhat weak argument, since it would apply only to the energy of light (whose inertia is already entailed by the electromagnetic relation E = pc), rather than to all forms of energy. However, Einstein’s paper actually describes a complete cyclical process, consisting first of the emission and absorption of the light pulse at opposite ends of a tube, and then the conveyance of that energy in any form whatsoever back to the emitting end of the tube by some arbitrary mechanism. If we were to assume that the energy itself conveys no mass or momentum on the return leg of the cycle, it would follow from the known momentum of the energy on the electromagnetic leg of the cycle that the tube will undergo a net impulse over this cycle, even though it has not been subjected to any external forces, and its internal state is restored on each cycle. As Einstein notes, this is not logically self-contradictory, but it clearly violates the conservation of momentum. We can restore momentum conservation if and only if the energy transfer in the return direction (with the energy in an arbitrary form, such as thermal energy in a pellet, for example) has the same momentum and equivalent mass as does the energy transfer by the electromagnetic pulse, which, as we’ve seen, is given by the relation E = Δmc2. |
|
|
|
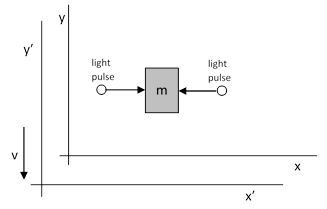
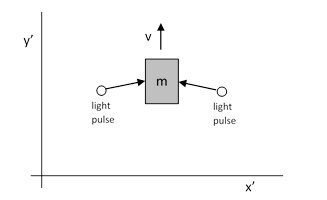
Einstein continued to devise various derivations of the mass-energy equivalence relation throughout his life, always striving to reduce this result of “extraordinarily theoretical importance” to the simplest possible terms. Interestingly, the last such derivation he published (1949) was essentially identical to the first (1905), except in reverse. He considered an object of mass m at rest with respect to a certain inertial coordinate system [x,y,t], and imagined two identical pulses of light striking this object from opposite directions and being absorbed by the object, as shown below. |
|
|
|
|
|
|
|
This is identical to the scenario in his 1905 paper, except that the directions of the light pulses have been reversed, i.e., they are being absorbed rather than emitted by the object. Now, just as in 1905, he considers the same situation with respect to the relatively moving system of inertial coordinates [x′,y′,t′]. In terms of these coordinates, the object is moving in the positive y’ direction with speed v, and the pulses of light also have a component of velocity in the positive y′ direction (aberration), as shown below. |
|
|
|
|
|
|
|
Again making use of the result from Maxwell’s equations that the momentum of a light pulse of energy E/2 is p = E/(2c), and noting that the component of this momentum in the positive y’ direction is (by Bradley’s aberration formula for small speeds) v/c times the whole momentum of the pulse, it follows that the absorbed momentum in the positive y′ direction from the two pulses is vE/c2. However, the velocity of the object doesn’t change when the pulses are absorbed, so, in order for the total momentum to be conserved, we must conclude that the inertial mass of the object has been increased by an amount Δm, increasing the momentum of the object by Δmv, which must equal the absorbed momentum vE/c2. Hence Δm = E/c2. |
|
|
|
This is a nice derivation, because it shows clearly how the finite speed of light and the consequent aberration leads directly to the conclusion that absorbed energy must contribute to the inertia of a material body. Of course, it still relies on the Maxwellian result that electromagnetic energy has momentum, and also on the conservation of momentum. To me, the most interesting thing about this derivation is not the similarity to the 1905 derivation, but the difference. In the earlier paper the object emits light in two opposite directions simultaneously, which shows that Einstein was already conceiving of electromagnetic radiation as a directed process, rather than the purely Maxwellian concept of spherical waves emanating in all directions. Of course, it has always been known that a ray of light can be directed, but on an elementary level (i.e., emission from excited atoms) it was not widely accepted in 1905 that light is a directed and localized phenomenon. Indeed it was Einstein’s own paper on the photo-electric effect in 1905 that introduced the idea of light quanta. |
|
|
|
One of the arguments that Einstein later used in support of light quanta was the argument of reversibility. He noted that, although we have reason to believe all fundamental physical processes are reversible in time, the usual conception of a spherical light waves emanating from a source does not appear to be an elementary reversible process. We can imagine an expanding spherical wave emanating outward from a source, but not a shrinking spherical wave converging on a receiver. He argued that it would make more sense to conceive of the elementary process of radiation as consisting of a reversible point-to-point exchange. Oddly enough, at another time (when debating with Ritz) he argued that a converging wave was not impossible, but simply very improbable, because it would require the coordinated actions of many separate sources, but he seems to have been ambivalent about this explanation. In any case, the 1905 derivation is based on the usual forward process of simultaneous emission in multiple directions from a single source, whereas the derivation published in 1949 is based on the reverse process of simultaneous absorption, presumably from coordinated sources. It’s interesting how the same themes recur in Einstein’s writings throughout his life. |
|
|