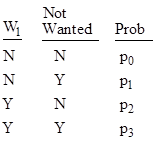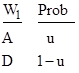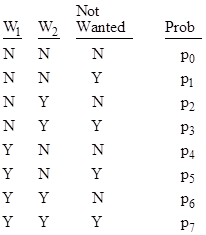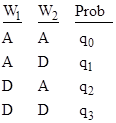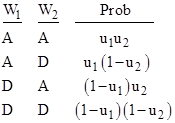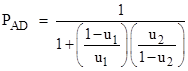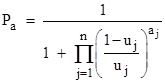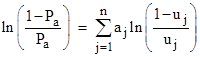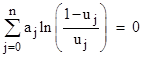Witness Words

Season your admiration for a while

With an attent ear till I may deliver,

Upon the witness of these gentlemen,

This marvel to you.

                                       Shakespeare

Suppose we want to create a filter to block unwanted messages, and we examine a large number of previous messages, classifying each one as wanted or unwanted. We also create a list of n “witness words”, W₁ to W_n, and we determine whether each of those words was or was not in each message. In principle we could then classify each message as one of the 2ⁿ⁺¹ possibilities represented by the presence or absence of each witness word and whether the message was wanted or unwanted. For example, with just a single witness word we have the four possibilities shown below.

Here the four probabilities are related by p₀ + p₁ + p₂ + p₃ = 1. Suppose we are only interested in whether the witness word is or is not a correct indicator. In that case each pair of complementary states is aggregated into a single state, so we have just two states, for Agree and Disagree, with probabilities u = p₀ + p₃ and 1 – u = p₁ + p₂ respectively, as tabulated below.

With two witness words we have the eight possibilities shown below:

Again if we focus purely on whether the words agree or disagree with the wantedness of the message, we aggregate the pairs of complementary states, and get the four states

where q₀ = p₀ + p₇, and so on. If we further assume that the probabilities of agreement for the words are statistically independent, then it follows that the probabilities for these four states can be expressed in terms of the individual probabilities of agreement for the words, which we will denote by u₁ and u₂ respectively. On this basis the probabilities are as shown below.

Now we ask the question:  If both of the witness words are giving the same testimony for a given message (i.e., if both are present or both are absent), what is the probability P_AA that their testimony is correct? The states for which both words give the same testimony are AA and DD, and the state for which they are both correct is AA, so the answer is the probability of AA divided by the probability of (AA or DD). Thus we have

Now suppose we ask a seemingly similar question:  If both witness words are present in a given message, what is the probability P_YY that their testimony is correct? To answer this question we must return to the fully articulated table of eight states, and note that the states with both words present are YYN and YYY, so the probability is

Recalling that q₀ = p₀ + p₇ and q₃ = p₁ + p₆, we see that P_YY equals P_AA if the probabilities of the two states in each complementary pair are equal to each other. (This implies, among other things, that the probability of W₁ being present given that the message is unwanted equals the probability that the message is unwanted given that W₁ is present.) If this complementarity holds, we can determine all the other probabilities for various combinations of presence or absence of the witness words. For example, if W₁ and W₂ disagree, the probability P_AD that W₁ is correct is equal to the probability of AD divided by the probability of (AD or DA), so we have

Dividing through by the numerator this can also be written as

If the complementarity condition holds, the same formula gives the probability of being unwanted given the presence of W₁ and absence of W₂. This immediately generalizes to any number n of witness words, and any specified combination of presences. Letting a_j = +1 or –1 accordingly as W_j is or is not present in a given message, we have

Re-arranging terms and taking the logarithm, it is sometimes convenient to write this in the additive form

Notice that values of u_j equal to 1/2 have no effect on the result. The overall symmetry is also notable, since we could let u₀ denote P_a and put a₀ = –1, and write the above equation as

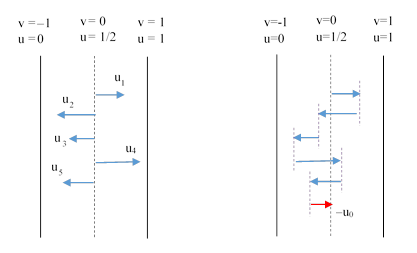
This shows that the probabilities of the individual words being present (or having valid testimony) are formally symmetrical with the probability of the overall message not being wanted. As discussed in another note, this equation is formally identical to the relativistic composition of velocities in one space dimension if we define v = 2u – 1. This maps the probability 1/2 to the velocity 0, and the overall probability range from 0 to 1 is mapped to the velocity range from -1 to +1. Pictorially we can depict each of the testimonies as a probability relative to the unwantedness null information state of 1/2, or equivalently as a velocity relative to the “frame” of the unwantedness as shown on the left below.

In the right hand figure the probabilities are “added” together using the formula derived above, and equivalently the velocities are “added” using the relativistic speed composition formula, to yield the final result u₀, and we can complete the set by including the last negative arrow from u₀ back to null. These effects, composed in any order, have a null “sum”, consistent with the symmetry of the formula.

Return to MathPages Main Menu