1.1  From Experience to Spacetime

I might revel in the world of intelligibility which still remains to me, but although I have an idea of this world, yet I have not the least knowledge of it, nor can I ever attain to such knowledge with all the efforts of my natural faculty of reason. It is only a something that remains when I have eliminated everything belonging to the senses… but this something I know no further… There must here be a total absence of motive - unless this idea of an intelligible world is itself the motive… but to make this intelligible is precisely the problem that we cannot solve.  

                                                                                                                     Immanuel Kant

We ordinarily take for granted the existence through time of objects moving according to fixed laws in three-dimensional space, but this is a highly abstract model of the objective world, far removed from the raw sense impressions that comprise our actual experience. This model may be consistent with our sense impressions, but it certainly is not uniquely determined by them. For example, Ptolemy and Copernicus constructed two very different conceptual models of the heavens based on essentially the same set of raw sense impressions. Likewise Weber and Maxwell synthesized two very different conceptual models of electromagnetism to account for a single set of observed phenomena. The fact that our raw sense impressions and experiences are (at least nominally) compatible with widely differing concepts of the world has led some philosophers to suggest that we should dispense with the idea of an "objective world" altogether, and base our physical theories on nothing but direct sense impressions, all else being merely the products of our imaginations. Berkeley expressed the positivist identification of sense impressions with objective existence by the famous phrase "esse est percipi" (to be is to be perceived). However, all attempts to base physical theories on nothing but raw sense impressions, avoiding arbitrary conceptual elements, invariably founder at the very start, because we have no sure means of distinguishing sense impressions from our thoughts and ideas. In fact, even the decision to make such a distinction represents a significant conceptual choice, one that is not strictly necessary on the basis of experience.

The process by which we, as individuals, learn to recognize sense impressions induced by an external world, and to distinguish them from our own internal thoughts and ideas, is highly complicated, and perhaps ultimately inexplicable. As Einstein put it (paraphrasing Kant) “the eternal mystery of the world is its comprehensibility”. Nevertheless, in order to examine the epistemological foundations of any physical theory, we must give some consideration to how the elements of the theory are actually derived from our raw sense impressions, without automatically interpreting them in conventional terms. On the other hand, if we suppress every pre-conceived notion, including ordinary rules of reasoning, we can hardly hope to make any progress. We must choose a level of abstraction deep enough to give a meaningful perspective, but not so deep that it can never be connected to conventional ideas.

As an example of a moderately abstract model of experience, we might represent an idealized observer as a linearly ordered sequence of states, each of which is a function of the preceding states and of a set of raw sense impressions from external sources. This already entails two profound choices. First, it is a purely passive model, in the sense that it does not invoke volition or free will. As a result, all conditional statements in this model must be interpreted only as correlations (as discussed more fully in section 3.2), because without freedom it is meaningless to talk about the different consequences of alternate hypothetical actions. Second, by stipulating that the states are functions of the preceding but not the subsequent states we introduce an inherent directional asymmetry to experience, even though the justification for this is far from clear.

Still another choice must be made as to whether the sequence of states and experiences is continuous or discrete. In either case we can parameterize the sequence by a variable l, and for the sake of definiteness we might represent each state S(l) and the corresponding sense impressions E(l) by strings of binary bits. Now, because of the mysterious comprehensibility of the world, it may happen that some functions of S are correlated with some functions of E. (Since this is a passive model by assumption, we cannot assert anything more than statistical correlations, because we do not have the freedom to arbitrarily vary S and determine the resulting E, but in principle we could still passively encounter enough variety of states and experiences to infer the most prominent correlations.) These most primitive correlations are presumably “hard-wired” into higher-level categories of senses and concepts (i.e., state variables), rather than being  sorted out cognitively. In terms of these higher-level variables we might find that over some range of l the sense impressions E(l) are strictly correlated with three functions q, f, a of the state S(l), which change only incrementally from one state to the next. Also, we may find that E is only incrementally different for incremental differences in q, f, a (independent of the prior values of those functions), and that this is the smallest and simplest set of functions with this property. Finally, suppose the sense impressions corresponding to a given set of values of the state functions are identical if the values of those functions are increased or decreased by some constant.

This describes roughly how an abstract observer might infer an orientation space along with the associated modes of interaction. In conventional terms, the observer infers the existence of external objects which induce a particular set of sense impressions depending on the observer’s orientation. (Of course, this interpretation is necessarily conjectural; there may be other, perhaps more complex, interpretations that correspond as well or better with the observer’s actual sequence of experiences.) At some point the observer may begin to perceive deviations from the simple three-variable orientation model, and find it necessary to adopt a more complicated conceptual model in order to accommodate the sequence of sense impressions. It remains true that the simple orientation model applies over sufficiently small ranges of states, but the sense impressions corresponding to each orientation may vary as a function of three additional state variables, which in conventional terms represent the spatial position of the observer. Like the orientation variables, these translation variables, which we might label x, y, and z, change only incrementally from one state to the next, but unlike the orientation variables there is no apparent periodicity.

Note that the success of this process of induction relies on a stratification of experiences, allowing the orientation effects to be discerned first, more or less independent of the translation effects. Then, once the orientation model has been established, the relatively small deviations from it (over small ranges of the state variable) could be interpreted as the effects of translatory motion. If not for this stratification (either in magnitude or in some other attribute), it might never be possible to infer the distinct sources of variation in our sense impressions. (On a more subtle level, the detailed metrical aspects of these translation variables will also be found to differ from those of the orientation variables, but only after quantitative units of measure and coordinates have been established.)

Another stage in the development of our hypothetical observer might be prompted by the detection of still more complicated variations in the experiential attributes of successive states. The observer may notice that while most of the orientation space is consistent with a fixed position, some particular features of their sense impressions do not maintain their expected relations to the other features, and no combination of the observer’s translation and orientation variables can restore consistency. The inferred external objects of perception can no longer be modeled based on the premise that their relations with respect to each other are unchanging. Significantly, the observer may notice that some features vary as would be expected if the observer’s own positional state had changed in one way, whereas other features vary as would be expected if the observer’s positions had changed in a different way. From this recognition the observer concludes that, just as he himself can translate through the space, so also can individual external objects, and the relations are reciprocal. Thus, to each object we now assign an independent set of translation coordinates for each state of the observer.

In so doing we have made another important conceptual choice, namely, to regard "external objects" as having individual identities that persist from one state to the next. Other interpretations are possible. For example, we could account for the apparent motion of objects by supposing that one external entity simply ceases to exist, and another similar entity in a slightly different position comes into existence. According to this view, there would be no such thing as motion, but simply a sequence of arrangements of objects with some similarities. This may seem obtuse, but according to quantum mechanics it actually is not possible to unambiguously map the identities of individual elementary particles (such as electrons) from one event to another (because their wave functions overlap). Thus the seemingly innocuous assumption of continuous and persistent identities for material objects through time is actually, on some level, demonstrably false. However, on the macroscopic level, physical objects do seem to maintain individual identities, or at least it is possible to successfully model our sense impressions based on the assumption of persistent identities (because the overlaps between wave functions are negligible), and this success is the justification for introducing the concept of motion for the objects of experience.

The conceptual model of our hypothetical observer now involves something that we may call distance, related to the translational state variables, but it’s worth noting that we have no direct perception of distances between ourselves and the assumed external objects, and even less between one external object and another. We have only our immediate sense impressions, which are understood to be purely local interactions, involving signals of some kind impinging on our senses. We infer from these signals a conceptual model of space and time within which external objects reside and move. This model actually entails two distinct kinds of extent, which we may call distance and length. An object, consisting of a locus of sense impressions that maintains a degree of coherence over time, has a spatial length, as do the paths that objects may follow in their motions, but the conceptual model of space also allows us to conceive of a distance between two objects, defined as the length of the shortest possible path between them.

The task of quantifying these distances, and of relating the orientation variables with the translation variables, then involves further assumptions. Since this is a passive model, all changes are strictly known only as a function of the single state variable, but we imagine other pseudo-independent variables based on the observed correlations. We have two means of quantifying spatial distances. One is by observing the near coincidence of one or more stable entities (measuring rods) with the interval to be quantified, and the other is to observe the change in the internal state variable as an object of stable speed moves from one end of the interval to the other. Thus we can quantify a spatial interval in terms of some reference spatial interval, or in terms of the associated temporal interval based on some reference state of motion. We identify these references purely by induction based on experience.

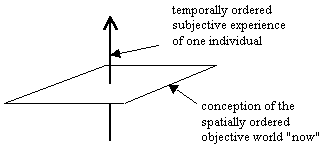
Combining the rotational symmetries and the apparent translational distances that we infer from our primary sense impressions, we conventionally arrive at a conception of the external world that is, in some sense, the dual of our subjective experience. In other words, we interpret our subjective experience as a one-dimensional temporally-ordered sequence of events, whereas we conceive of "the objective world now" corresponding to a single perceived event as a three-dimensional expanse of space as illustrated below:

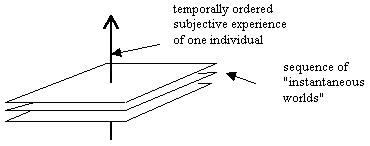
In this way we intuitively conceive of time and space as inherently perpendicular dimensions, but complications arise if we posit that each event along our subjective path resides in, and is an element of, an objective world. If the events along any path are discrete, then we might imagine a simple sequence of discrete "instantaneous worlds":

One difficulty with this arrangement is that it isn't clear how (or whether) these worlds interact with each other. If we regard each "instant" as a complete copy of the spatial universe, separate from every other instant, then there seems to be no definite way to identify an object in one world with "the same" object in another, particularly considering qualitatively identical objects such as electrons. If we have two electrons assigned the labels A and B in one instant of time, and if we find two electrons in the next instant of time, we have no certain way of deciding which of them was the "A" electron from the previous instant. (In fact, we cannot even map the spatial locations of one instant to "the same" locations in any other instant.) This illustrates how the classical concept of motion is necessarily based on the assumption of persistent identities of objects from one instant to another.  Since it does seem possible (at least in the classical realm) to organize our experiences in terms of individual objects with persistent and unambiguous identities over time, we may be led to suspect that the sequence of existence of an individual or object in any one instant must be, in some sense, connected to or contiguous with its existence in neighboring instants. If these objects are the constituents of "the world", this suggests that space itself at any "instant" is continuous with the spaces of neighboring instants. This is important because it implies a definite connectivity between neighboring world-spaces, and this, as we'll see, places a crucial constraint on the relativity of motion.

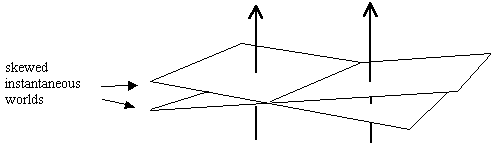
Another complication concerns the relative orderings of world-instants along different paths.  Our schematic above implied that the "instantaneous worlds" are well-ordered in the sense that they are encountered in the same order along every individual's path, but of course this need not be the case. For example, we could equally well imagine an arrangement in which the "instantaneous worlds" are skewed, so that different individuals encounter them in different orders, as illustrated below.

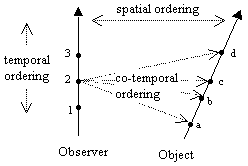
The concept of motion assumes the world can be analyzed in two different ways, first as the union of a set of mutually exclusive "events", and second as a set of "objects" each of which participates in an ordered sequence of events. In addition to this ordering of events encountered by each individual object, we must also assume both a co-lateral ordering of the events associated with different objects, and a transverse ordering of events from one object to another. These three kinds of orderings are illustrated schematically below.

This diagram suggests that the idea of motion is actually quite complex, even in this simple abstract model. Intuitively we regard motion as something like the derivative of the spatial "position" with respect to "time", but we can't even unambiguously define the distance between two worldlines, because it depends on how we correlate the temporal ordering along one line to the temporal ordering along the other. Essentially our concept of motion is overly ambitious, because we want it to express the spatial distance from the observer to the object for each event along the observer's worldline, but the intervals from one worldline to another are not confined to the worldlines themselves, so we have no definite way of assigning those intervals to events along our worldline. The best we can do is correlate all the intervals from a particular point on the observer's worldline to the object's worldline.

When we considered everything in terms of the sense impressions of just a single observer this was not an issue, since only one parameterization was needed to map the experiences of that observer, interpreted solipsistically. Any convenient parameterization was suitable. When we go on to consider multiple observers and objects we can still allow each observer to map his experiences and internal states using the most convenient terms of reference (which will presumably include his own state-index as the temporal coordinate), but now the question arises as to how all these private coordinate systems are related to each other. To answer this question we need to formalize our parameterizations into abstract systems of coordinates, and then consider how the coordinates of any given event with respect to one system are related to the coordinates of the same event with respect to another system. This is discussed in the next section.

Considering how far removed from our raw sense impressions is our conceptual model of the external world, and how many unjustified assumptions and interpolations are involved in its construction, it’s easy to see why some philosophers have advocated the rejection of all conceptual models. However, the fact remains that the imperative to reconcile our experience with some model of an objective external world has been one of the most important factors guiding the development of physical theories. Even in quantum mechanics, arguably the field of physics most resistant to complete realistic reconciliation, we still rely on the "correspondence principle", according to which the observables of the theory must conform to the observables of classical realistic models in the appropriate limits. Naturally our interpretations of experience are always provisional, being necessarily based on incomplete induction, but conceptual models of an objective world have proven (so far) to be indispensable.

Return to Table of Contents