1.3  Inertia and Relativity

These or none must serve for reasons, and it is my great happiness that examples prove not rules, for to confirm this opinion, the world yields not one example.

                                                                                                                John Donne

In his treatise "On the Revolution of Heavenly Spheres" Copernicus argued for the conceivability of a moving Earth by noting that

...every apparent change in place occurs on account of the movement either of the thing seen or of the spectator, or on account of the necessarily unequal movement of both. No movement is perceptible relatively to things moved equally in the same direction - I mean relatively to the thing seen and the spectator... As the ship floats along the calm, all external things seem to have the motion that is really that of the ship, while those within the ship feel that they and all its contents are at rest....

The first part of this quote suggests a purely kinematical and relational conception of relativity (like that of Aristarchus), based simply on the idea that we judge the positions of objects only in relation to other objects. However, the “thought experiment” involving a ship floating “along the calm” hints at a more sophisticated concept of relativity based on the principle of inertia, even though Copernicus was in no position to justify this analogy with a theory of dynamics. Hence the hypothesis of a moving Earth was vulnerable to the objection that we do not directly “sense” any such motion. Partly to answer this objection, Galileo began the development of the modern concept of inertia, on the basis of which Copernicus’s claim about the behavior of objects inside a ship moving at some constant speed in a straight line can be justified. Galileo pointed out that

... among things which all share equally in any motion, [that motion] does not act, and is as if it did not exist... in throwing something to your friend, you need throw it no more strongly in one direction than in another, the distances being equal... jumping with your feet together, you pass equal spaces in every direction...

Thus Galileo's approach was based on a dynamical rather than a merely kinematic analysis, because he refers to forces acting on bodies, asserting that the dynamic behavior of bodies is homogeneous and isotropic in terms of (suitably defined) measures in any uniform state of motion. This soon led to the modern principle of inertial relativity, although Galileo himself seems never to have fully grasped the distinction between accelerated and unaccelerated motion. He believed, for example, that circular motion was a natural state that would persist unless acted upon by some external agent. This shows that the resolution of dynamical behavior into inertial and non-inertial components – which we generally take for granted today – is more subtle than it may appear. As Newton wrote:

...the whole burden of philosophy seems to consist in this: from the phenomena of motions to infer the forces of nature, and then from these forces to deduce other phenomena...

Newton’s doctrine implicitly assumes that forces can be inferred from the motions of objects, but establishing the correspondence between forces and motions is not trivial, because the doctrine is, in a sense, circular. We infer “the forces of nature” from observed motions, and then we account for observed motions in terms of those forces. This assumes we can distinguish between forced and unforced motion, but there is no a priori way of making such a distinction. For example, the roughly circular motion of the Moon around the Earth might suggest the existence of a force (universal gravitation) acting between these two bodies, but it could also be taken as an indication that circular motion is a natural form of unforced motion, as Galileo believed. Different definitions of unforced motion lead to different sets of implied “forces of nature”. The task is to choose a definition of unforced motion that leads to the identification of a set of physical forces that gives the most intelligible accounting of the phenomena. By indirect reasoning, the natural philosophers of the seventeenth century eventually arrived at the idea that, in the complete absence of external forces, an object would move uniformly in a straight line, and that, therefore, whenever we observe an object whose speed or direction of motion is changing, we can infer that an external force – proportional to the rate of change of motion – is acting upon that object. This is the principle of inertia, the most successful principle ever proposed for organizing our knowledge of the natural world. Notice that it refers to how a free object “would” move, because no object in our experience is completely free from all external forces. Thus the conditions of this fundamental principle, as stated, are never actually met, which highlights the subtlety of Newton’s doctrine, and the aptness of his assertion that it comprises “the whole burden of philosophy”. Also, notice that the principle of inertia does not discriminate between different states of uniform motion in straight lines, so it automatically entails a principle of relativity of dynamics, and in fact the two are essentially synonymous.

One of the first explicit statements of the modern principle of inertial relativity was made by Pierre Gassendi, who is most often remembered today for reviving the ancient Greek doctrine of atomism. In the 1630's Gassendi repeated many of Galileo's experiments with motion, and interpreted them from a more abstract point of view, consciously separating out gravity as an external influence, and recognizing that the remaining "natural states of motions" were characterized not only by uniform speeds (as Galileo had said) but also by rectilinear paths. In order to conceive of inertial motion, it is necessary to review the whole range of observable motions of material objects and imagine those motions if the effects of all known external influences were removed. From this resulting set of ideal states of motion, it is necessary to identify the largest possible "equivalence class" of relatively uniform and rectilinear motions. These motions and configurations then constitute the basis for inertial measurements of space and time, i.e., inertial coordinate systems. Naturally inertial motions will then necessarily be uniform and rectilinear with respect to these coordinate systems, by definition.

Shortly thereafter (1644), Descartes presented the concept of inertial motion in his "Principles of Philosophy":

Each thing...continues always in the same state, and that which is once moved always continues to move...and never changes unless caused by an external agent... all motion is of itself in a straight line...every part of a body, left to itself, continues to move, never in a curved line, but only along a straight line.

Similarly, in Huygens' "The Motion of Colliding Bodies" (composed in the mid 1650's but not published until 1703), the first hypothesis was that

Any body already in motion will continue to move perpetually with the same speed in a straight line unless it is impeded.

Ultimately Newton incorporated this principle into his masterpiece, "Philosophiae Naturalis Principia Mathematica" (The Mathematical Principles of Natural Philosophy), as the first of his three “laws of motion"

1) Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by the forces impressed upon it.

2) The change of motion is proportional to the motive force impressed, and is made in the direction of the right line in which that force is impressed.

3) To every action there is always opposed an equal and opposite reaction; or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.

These “laws” express the classical mechanical principle of relativity, asserting equivalence between the conditions of "rest" and "uniform motion in a right line". Since no distinction is made between the various possible directions of uniform motion, the principle also implies the equivalence of uniform motion in all directions in space. Thus, if everything in the universe is a "body" in the sense of this law, and if we stipulate rules of force (such as Newton's second and third laws) that likewise do not distinguish between bodies at rest and bodies in uniform motion, then we arrive at a complete system of dynamics in which, as Newton said, "absolute rest cannot be determined from the positions of bodies in our regions". Corollary 5 of Newton’s Principia states

The motions of bodies included in a given space are the same among themselves, whether that space is at rest or moves uniformly forwards in a straight line without circular motion.

Of course, this presupposes that the words "uniformly" and "straight" have unambiguous meanings. Our concepts of uniform speed and straight paths are ultimately derived from observations of inertial motions, so the “laws of motion” are to some extent circular. These laws were historically expressed in terms of inertial coordinate systems, which in turn are defined by the laws of motion. In other words, we define an inertial coordinate system as a system of space and time coordinates in terms of which inertia is homogeneous and isotropic, and then we announce the “laws of motion”, which assert that inertia is homogeneous and isotropic with respect to inertial coordinate systems. Thus the “laws of motion” are true by definition. Their significance lies not in their truth, which is trivial, but in their applicability. The empirical fact that there exist systems of inertial coordinates is what makes the concept significant. We have no a priori reason to expect that such coordinate systems exist, i.e., that the forces of nature would resolve themselves so coherently on this (or any other finite) basis, but they evidently do. In fact, it appears that not just one such coordinate system exists (which would be remarkable enough), but that infinitely many of them exist, in all possible states of relative motion. To be precise, the principle of relativity asserts that for any material particle in any state of motion there exists an inertial coordinate system in terms of which the particle is (at least momentarily) at rest.

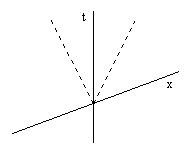
It’s important to recognize that Newton’s first law, by itself, is not sufficient to identify the systems of coordinates in terms of which all three laws of motion are satisfied. The first law serves to determine the shape of the coordinate axes and inertial paths, but it does not fully define a system of inertial coordinates, because the first law is satisfied in infinitely many systems of coordinates that are not inertial coordinates in the sense defined above. The system of oblique xt coordinates illustrated below is an example of such a system.

The two dashed lines indicate the paths of two identical objects, both initially at rest with respect to these coordinates and propelled outward from the origin by impulses of equal magnitude (acting against each other). Every object not subject to external forces moves with uniform speed in a straight line with respect to this coordinate system, so Newton's First Law of motion is satisfied, but the second law clearly is not, because the speeds imparted to these identical objects by equal forces are not equal. In other words, inertia is not isotropic with respect to these coordinates. In order for Newton's Second Law to be satisfied, we not only need the coordinate axes to be straight and uniformly graduated relative to freely moving objects, we need the space axes to be aligned in time such that mechanical inertia is the same in all spatial directions (so that, for example, the objects whose paths are represented by the two dashed lines in the above figure have the same speeds). This effectively establishes the planes of simultaneity of inertial coordinate systems. In an operational sense, Newton's Third Law is also involved in establishing the planes of simultaneity for an inertial coordinate system, because it is only by means of the Third Law that we can actually define "equal forces" as the forces necessary to impart equal "quantities of motion" (to use Newton’s phrase). Of course, this doesn't imply that inertial coordinate systems are the "true" systems of reference. They are simply the most intuitive, convenient, and readily accessible systems, based on the inertial behavior of material objects.

In addition to contributing to the definition of an inertial coordinate system, the third law also serves to establish a fundamental aspect of the relationships between relatively moving inertial coordinate systems. Specifically, the third law implies (requires) that if the spatial origin of one inertial coordinate system is moving at velocity v with respect to a second inertial coordinate system, then the spatial origin of the second system is moving at velocity -v with respect to the first. This property is sometimes called reciprocity, and is important for the various derivations of the Lorentz transformation to be presented in subsequent sections.

Based on the definition of an inertial coordinate system, and the isotropy of inertia with respect to such coordinates, it follows that two identical objects, initially at rest with respect to those coordinates and exerting a mutual force on each other, recoil by equal distances in equal times (in accord with Newton’s third law). Assuming the lengths of stable material objects are independent of their spatial positions and orientations (spatial homogeneity and isotropy), it follows that we can synchronize distant clocks with identical particles ejected with equal forces from the mid-point between the clocks. This operational definition of simultaneity is not new. It is precisely what Galileo described in his illustration of inertial motion onboard a moving ship. When he wrote that an object thrown with equal force will reach equal distances [in the same time], he was implicitly defining simultaneity at separate locations on the basis of inertial isotropy. This is crucial to understanding the significance of inertial coordinate systems. The requirement for a particular object to be at rest with respect to the system suffices only to determine the direction of the "time axis", i.e., the loci of constant spatial position. Galileo and his successors realized (although they did not always explicitly state) that it is also necessary to specify the loci of constant temporal position, and this is achieved by choosing coordinates in such a way that mechanical inertia is isotropic. (This means the inertia of an object does not depend on any absolute reference direction in space, although it may depend on the velocity of the object. It is sufficient to say the resistance to acceleration of a resting object is the same in all spatial directions.)

Conceptually, to establish a complete system of space and time coordinates based on inertial isotropy, imagine that at each point in space there is an identically constructed cannon, and all these cannons are at rest with respect to each other. At one particular point, which we designate as the origin of our coordinates, is a clock and numerous identical cannons, each pointed at one of the other cannons out in space. The cannons are fired from the origin, and when a cannonball passes one of the external cannons it triggers that external cannon to fire a reply back to the origin. Each cannonball has identifying marks so we can correlate each reply with the shot that triggered it, and with the identity of the replying cannon. The ith reply event is assigned the time coordinate t_i = [t_return(i) - t_send(i)]/2 seconds, and it is assigned space coordinates x_i, y_i, z_i based on the angular direction of the sending cannon and the radial distance r_i = t_i cannon-seconds. This procedure would have been perfectly intelligible to Newton, and he would have agreed that it yields an inertial coordinate system, suitable for the application of his three laws of motion.

Naturally given one such system of coordinates, we can construct infinitely many others by simple spatial re-orientation of the space axes and/or translation of the spatial or temporal axes. All such transformations leave the speed of every object unchanged. An equivalence class of all such inertial coordinate systems is called an inertial reference frame. For characterizing the mutual dynamical states of two material bodies, the associated inertial rest frames of the bodies are more meaningful than the mere distance between the bodies, because any inertial coordinate system possesses a fixed spatial orientation with respect to any other, enabling us to take account of tangential motion between bodies whose mutual distance is not changing. For this reason, the physically meaningful "relative velocity of two material bodies" is best defined as their reciprocal states of motion with respect to each others' associated inertial rest frame coordinates.

The principle of relativity does not tell us how two relatively moving systems of inertial coordinates are related to each other, but it does imply that this relationship can be determined empirically. We need only construct two relatively moving systems of inertial coordinates and compare them. Based on observations of coordinate systems with relatively low mutual speeds, and with the limited precision available at the time, Galileo and Newton surmised that if (x,t) is an inertial coordinate system then so is (xʹ,tʹ), where

and v is the mutual speed between the origins of the two systems. This implies that relative speeds are simply additive. In other words, if a material object B is moving at the speed v in terms of inertial rest frame coordinates of A, and if an object C is moving in the same direction at the speed u in terms of inertial rest frame coordinates of B, then C is moving at the speed v + u in terms of inertial rest frame coordinates of A. This conclusion may seem plausible, but it's important to realize that we are not free to arbitrarily adopt this or any other transformation and speed composition rule for the set of inertial coordinate systems, because those systems are already fully defined (up to conventional scale factors) by the requirements for inertia to be homogeneous and isotropic and for momentum to be conserved. These properties suffice to determine the set of inertial coordinate systems and (therefore) the relationships between them. Given these conditions, the relationship between relatively moving inertial coordinate systems, whatever it may be, is a matter of empirical fact.

Of course, inertial isotropy is not the only possible basis for constructing spacetime coordinate systems. We could impose a different constraint to determine the loci of constant temporal position, such as a total temporal ordering of events. However, if we do this, we will find that mechanical inertia is generally not isotropic in terms of the resulting coordinate systems, so the usual symmetrical laws of mechanics will not be valid in terms of those coordinate systems (at least not if restricted to ponderable matter).  Indeed this was the case for the ether theories developed in the late 19th century, as discussed in subsequent sections. Such coordinate systems, while extremely awkward, would not be logically inconsistent. The choices we make to specify a coordinate system and to resolve spacetime intervals into separate spatial and temporal components are to some extent conventional, provided we are willing to disregard the manifest symmetry of physical phenomena. But since physics consists of identifying and understanding the symmetries of nature, the option of disregarding those symmetries does not appeal to most physicists.

By the end of the nineteenth century a new class of phenomena involving electric and magnetic fields had been incorporated into physics, and the concept of inertia was found to be applicable to these phenomena as well. For example, Maxwell’s equations imply that a pulse of light conveys momentum. Hence the principle of inertia ought to apply to electromagnetism as well as to the motions of material bodies. In his 1905 paper “On the Electrodynamics of Moving Bodies” Einstein adopted this more comprehensive interpretation of inertia, basing the special theory of relativity on the proposition that

The laws by which the states of physical systems undergo changes are not affected, whether these changes of state be referred to the one or the other of two systems of [inertial] coordinates in uniform translatory motion.

This is nearly identical to Newton’s Corollary 5. It’s unfortunate that the word "inertial" was omitted, because, as noted above, uniform translatory motion is not sufficient to ensure that a system of coordinates is actually an inertial coordinate system in the full sense. However, Einstein made it clear that he was indeed talking about inertial coordinate systems when he previously characterized them as coordinate systems “in which the equations of Newtonian mechanics hold good”. Admittedly this is a somewhat awkward assertion in the context of Einstein’s paper, because one of the main conclusions of the paper is that the equations of Newtonian mechanics do not precisely “hold good” with respect to inertial coordinate systems. Recognizing this inconsistency, Sommerfeld added a footnote in subsequent published editions of Einstein’s paper, qualifying the statement about Newtonian mechanics holding good “to the first approximation”, but this footnote does not really clarify the situation. Fundamentally, the class of coordinate systems that Einstein was trying to identify (the inertial coordinate systems) are those in terms of which inertia is homogeneous and isotropic, meaning that free objects move at constant speed in straight lines and (just as importantly) the force required to accelerate an object from rest to a given speed is the same in all directions. As discussed above, these conditions are just sufficient to determine a coordinate system in terms of which the symmetrical equations of mechanics hold good, but without pre-supposing the exact form of those equations.

Since light (i.e., an electromagnetic wave) carries momentum, and the procedure for constructing an inertial coordinate system described previously was based on the isotropy of momentum, it is reasonable to expect that pulses of light could be used in place of cannonballs, and we should arrive at essentially the same class of coordinate systems. In his 1905 paper this is how Einstein described the construction of inertial coordinate systems, tacitly asserting that the propagation of light is isotropic with respect to the same class of coordinate systems in terms of which mechanical inertia is isotropic. In this respect it might seem as if he was treating light as a stream of inertial particles, and indeed his paper on special relativity was written just after the paper in which he introduced the concept of photons. However, we know that light is not exactly like a stream of material particles, especially because we cannot conceive of light being at rest with respect to any system of inertial coordinates. The way in which light fits into the framework of inertial coordinate systems is considered in the next section. We will find that although the principle of relativity continues to apply, and the definition of inertial coordinate systems remains unchanged, the relationship between relatively moving systems of inertial coordinate systems must be different than what Galileo and Newton surmised.

Return to Table of Contents