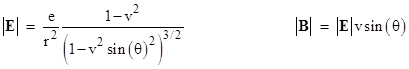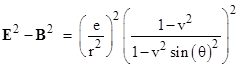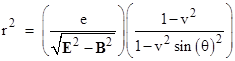1.5  Corresponding States

It would be more satisfactory if it were possible to show by means of certain fundamental assumptions – and without neglecting terms of any order – that many electromagnetic actions are entirely independent of the motion of the system. Some years ago I already sought to frame a theory of this kind. I believe it is now possible to treat the subject with a better result.

                                                                   H. A. Lorentz, 1904

It appears that the impossibility of detecting the absolute motion of the Earth by experiment may be a general law of nature; we are naturally inclined to admit this law, which we will call the ‘Postulate of Relativity’, without restriction. Whether or not this postulate, which up to now agrees with experiment, may later be corroborated or disproved by experiments of greater precision, it is interesting in any case to ascertain its consequences.

                                                                    H. Poincare, 1905

In 1889 Oliver Heaviside deduced from Maxwell’s equations that the electric and magnetic fields on a spherical surface of radius r surrounding a uniformly moving electric charge e are radial and circumferential respectively, with magnitudes

where θ is the angle relative to the direction of motion with respect to the stationary frame of reference. (We have set c = 1 for clarity.) The left hand equation implies that, in comparison with a stationary charge, the electric field strength at a distance r from a moving charge is less by a factor of 1–v² in the direction of motion, and greater by a factor of 1/(1–v²)^1/2 in the perpendicular directions. Thus the strength of the electric field of a moving charge is anisotropic. These equations imply that

which Heaviside recognized as the convection potential, i.e., the scalar field whose gradient is the total electromagnetic force on a co-moving charge at that relative position. This scalar is invariant under Lorentz transformations, and it follows from the above formula that the cross-section of surfaces of constant potential are described by

This is the equation of an ellipse, so Heaviside’s formulas imply that the surfaces of constant potential are ellipsoids, shortened in the direction of motion by the factor (1–v²)^1/2. From the modern perspective the contraction of characteristic lengths in the direction of motion is an immediate corollary of the fact that Maxwell’s equations are Lorentz covariant, but at the time the idea of anisotropic changes in length due to motion was regarded as a peculiar and somewhat unexpected attribute of electromagnetic fields. It wasn’t until 1896 that Searle explicitly pointed out that Heaviside’s formulas imply the contraction of surfaces of constant potential into ellipsoids, but already in 1889 it seems that Heaviside’s findings had prompted an interesting speculation as to the deformation of stable material objects in uniform motion.

George Fitzgerald corresponded with Heaviside, and learned of the anisotropic variations in field strengths for a moving charge, and this was at the very time when he was struggling to understand the null result of the latest Michelson and Morley ether drift experiment (performed in 1887). It occurred to Fitzgerald that the null result would be explained if the material comprising Michelson’s apparatus contracts in the direction of motion by the factor (1–v²)^1/2, and moreover that this contraction was not entirely implausible, because, as he wrote in a brief letter to the American journal Science in 1889

We know that electric forces are affected by the motion of the electrified bodies relative to the ether and it seems a not improbable supposition that the molecular forces are affected by the motion and that the size of the body alters consequently.

A few years later (1892) Lorentz independently came to the same conclusion, and proceeded to explain in detail how the variations in the electromagnetic field implied by Maxwell’s equations actually result in a proportional contraction of matter – at least if we assume the forces responsible for the stability of matter are affected by motion in the same way as the forces of electromagnetism. This latter assumption Lorentz called the “molecular force hypothesis”, admitting that he had no real justification for it (other than the fact that it accounted for Michelson’s null result). On the basis of this hypothesis, Lorentz showed that the description of the equilibrium configuration of a uniformly moving material object in terms of its “local coordinates” is identical to the description of the same object at absolute rest in terms of the ether rest frame coordinates. He called this the theorem of corresponding states.

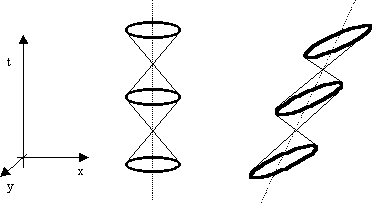
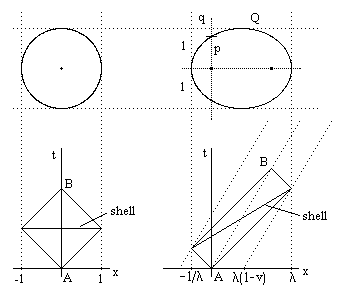
To illustrate, consider a small bound spherical configuration of matter at rest in the ether. We assume the forces responsible for maintaining the spherical structure of this particle are affected by uniform motion through the ether in exactly the same way as are electromagnetic forces, which is to say, they are covariant with respect to Lorentz transformations. These forces may propagate at any speed (at or below the speed of light), but it is most convenient for descriptive purposes to consider forces that propagate at precisely the speed of light (in terms of the fixed rest frame coordinates of the ether), because this automatically ensures Lorentz covariance. A wave emanating from the geometric center of the particle at the speed c would expand spherically until reaching the radius of the configuration, where we can imagine that it is reflected and then contracts spherically back to a point (like a spatial filter) and re-expands on the next cycle. This is illustrated by the left-hand cycle below.

Only two spatial dimensions are shown in this figure. (In four-dimensional spacetime each shell is actually a sphere.) Now, if we consider an intrinsically identical configuration of matter in uniform motion relative to the putative rest frame of the ether, and if the equilibrium shape is maintained by forces that are Lorentz covariant, just as is the propagation of electromagnetic waves, then it must still be the case that an electromagnetic wave can expand from the center of the configuration to the perimeter, and be reflected back to the center in a coherent pattern, just as for the stationary configuration. This implies that the absolute shape of the configuration must change from a sphere to an ellipsoid, as illustrated by the right-hand figure above. The spatial size of the particle in terms of the ether rest frame coordinates is just the intersection of a horizontal time slice with the region swept out by the perimeter of the configuration. For any given characteristic particle, since there is no motion relative to the ether in the transverse direction, the size in the transverse direction must be unaffected, so the widths of the configurations in the "y" direction are equal. The figure below shows more detailed side and top views of one cycle of a stationary and a moving particle (with motions referenced to the rest frame of the putative ether).

It's understood that these represent corresponding states, i.e., intrinsically identical equilibrium configurations of matter, whose spatial shapes are maintained by Lorentz covariant forces. In each case the geometric center of the configuration progresses from point A to point B in the respective figure. The right-hand configuration is moving with a speed v in the positive x direction. It can be shown that the transverse sizes of the configurations are equal if the projected areas of the cross-sectional side views (the lower figures) are equal. This is also a consequence of the fact that the enclosed space-time volume is invariant, which it must be for a linear transformation that depends only on v and that is the same at all places and in all directions. (As an aside, we recall that one of the early rivals to Lorentz’s electron theory was the theory of Bucherer and Langevin, who proposed that an electron contracts in the direction of motion and expands in the transverse directions so as to maintain constant spatial volume. In retrospect we can see that Lorentz’s theory also implies a constant volume for the electron – but it is a constant spacetime volume.) Thus, light emanating from point A of the moving particle extends a distance 1/λ to the left and a distance λ to the right, where λ is a constant function of v. Specifically, we must have

where we have set c = 1 for clarity. The leading edge of the shaft swept out by the moving shell crosses the x axis at a distance λ(1–v) from the center point A, which implies that the object's instantaneous spatial extent from the center to the leading edge is only

Likewise it's easy to see that the elapsed time (according to the putative ether rest frame coordinates) for one cycle of the moving particle, i.e., from point A to point B, is simply

compared with an elapsed time of 2 for the same particle at rest. Hence we unavoidably arrive at Fitzgerald's length contraction and Lorentz's local time dilation for objects in motion with respect to the x,y,t coordinates, provided only that all characteristic spatial and temporal intervals associated with physical entities are maintained by forces that are Lorentz covariant.

The above discussion did not invoke Maxwell’s equations at all, except to the extent that those equations suggested the idea that all the fundamental forces are Lorentz covariant. Furthermore, we have so far omitted consideration of one very important force, namely, the force of inertia. We assumed the equilibrium configurations of matter were maintained by certain forces, but if we consider oscillating configurations, we see that the periodic shapes of such configurations depend not only on the binding force(s) but also on the inertia of the particles. Therefore, in order to arrive at a fully coherent theorem of corresponding states, we must assume that inertia itself is Lorentz covariant. As Lorentz wrote in his 1904 paper

…the proper relation between the forces and the accelerations will exist… if we suppose that the masses of all particles are influenced by a translation to the same degree as the electromagnetic masses of the electrons.

In other words, we must assume the inertial mass (resistance to acceleration) of every particle is Lorentz covariant, which implies that the mass has transverse and longitudinal components that vary in a specific way when the particle is in motion. Now, it was known that some portion of a charged object’s resistance to acceleration is due to self-induction, because a moving charge constitutes an electric current, which produces a magnetic field, which resists changes in the current. Not surprisingly, this resistance to acceleration is Lorentz covariant, because it is a purely electromagnetic effect. At one time it was thought that perhaps all mass (even of electrically neutral particles) might be electromagnetic in origin, and some even hoped that gravity and the unknown forces governing the stability of matter would also someday be shown to be electromagnetic, leading to a totally electromagnetic world view. (Ironically, at this same time, others were trying to maintain the mechanical world view, by seeking to explain the phenomena of electromagnetism in terms of mechanical models.) If in fact all physical effects are ultimately electromagnetic, one could plausibly argue that Lorentz had succeeded in developing a constructive account of relativity, based on the known properties of electromagnetism. Essentially this would have resolved the apparent conflict between the Galilean relativity of mechanics and Lorentzian relativity of electromagnetism by asserting that there is no such thing as mechanics, there is only electromagnetism. Then, since electromagnetism is Lorentz covariant, it would follow that everything is Lorentz covariant.

However, it was already known (though perhaps not well known) when Lorentz wrote his paper in 1904 that the electromagnetic world view is not tenable. Poincare pointed this out in his 1905 Palermo paper, in which he showed that the assumption of a purely electromagnetic electron was self-consistent only with the degenerate solution of no charge density at all. Essentially, the linearity of Maxwell’s equations implies that they can not possibly yield stable bound configurations of charge. Poincare wrote

We must then admit that, in addition to electromagnetic forces, there are also non-electromagnetic forces or bonds. Therefore, we need to identify the conditions that these forces or bonds must satisfy for electron equilibrium to be undisturbed by the [Lorentz] transformation.

In the remainder of this remarkable paper, Poincare derives general conditions that Lorentz covariant forces must satisfy, and considers in particular the force of gravity. The most significant point is that Poincare had recognized that Lorentz had reached the limit of his constructive approach, and instead he (Poincare) was proceeding not to deduce the necessity of relativity from the phenomena of electromagnetism or gravity, but rather to deduce the necessary attributes of electromagnetism and gravity from the principle of relativity. In this sense it is fair to say that Poincare originated a theory of relativity in 1905 (simultaneously with Einstein). On the other hand, both Poincare and Lorentz continued to espouse the view that relativity was only an apparent fact, resulting from the circumstance that our measuring instruments are necessarily affected by absolute motion in the same way as are the things being measured. Thus they believed that the speed of light was actually isotropic only with respect to one single inertial frame of reference, and it merely appeared to be isotropic with respect to all the others. Of course, Poincare realized full well (and indeed was the first to point out) that the Lorentz transformations form a group, and the symmetry of this group makes it impossible, even in principle, to single out one particular frame of reference as the true absolute frame (in which light actually does propagate isotropically). Nevertheless, he and Lorentz both argued that there was value in maintaining the belief in a true absolute rest frame, and this point of view has continued to find adherents down to the present day.

As a historical aside, Oliver Lodge claimed that Fitzgerald originally suggested the deformation of bodies as an explanation of Michelson’s null result

…while sitting in my study at Liverpool and discussing the matter with me. The suggestion bore the impress of truth from the first.

Interestingly, Lodge interpreted Fitzgerald as saying not that objects contract in the direction of motion but that they expand in the transverse direction. We saw in the previous section how Voigt’s derivation of the Lorentz transformation left the scale factor undetermined, and the evaluation of this factor occupied a surprisingly large place in the later writings of Lorentz, Poincare, and Einstein. In his book The Ether of Space (1909) Lodge provided an explanation for why he believed the effect of motion should be a transverse expansion rather than a longitudinal contraction. He wrote

When a block of matter is moving through the ether of space its cohesive forces across the line of motion are diminished, and consequently in that direction it expands…

Lodge’s reliability is suspect, since he presents this as an “explanation” not only of Fitzgerald’s suggestion but also of Lorentz’s theory, which it definitely is not. But more importantly, Lodge’s misunderstanding highlights one of the drawbacks of conceiving of the deformation effect as arising from variations in electromagnetic forces. In order to give a coherent account of phenomena, the lengths of objects must vary in exactly the same proportion as the distances between objects. It would be quite strange to suppose that the transverse distances between (neutral and widely separated) objects would increase by virtue of being set in motion along parallel lines. In fact, it is not clear what this would even mean. If three or more objects were set in parallel motion, in which direction would they be deflected? And what could be the cause of such a deflection? Neutral objects at rest exert a small attractive force on each other (due to gravity), but diminishing this net force of cohesion would obviously not cause the objects to repel each other.

Oddly enough, if Lodge had focused on the temporal instead of the spatial effects of motion, his reasoning would have approximated a valid justification for time dilation. This justification is often illustrated in terms two mirrors in parallel motion, with a pulse of light bouncing between them. In this case the motion of the mirrors actually does diminish the frequency of bounces, relative to the stationary ether frame, because the light must travel further between each reflection. Thus the time intervals “expand” (i.e., dilate). Given this time dilation of the local moving coordinates, it’s fairly obvious that there must be a corresponding change in the effective space coordinate (since spatial lengths are directly related to time intervals by dx = vdt). In other words, if an observer moves at speed v relative to the ground, and passes over an object of length L at rest on the ground, the length of the object as assessed by the moving observer is affected by his measure of time. Since he is moving at speed v, the length of the object is vdt, where dt is the time it takes him to traverse the length of the object – but which "dt" will he use? Naturally if he bases his length estimate on the measure of the time interval recorded on a ground clock, he will have dt = L/v, so he will judge the object to be v(L/v) = L units in length. However, if he uses his own effective time as indicated on his own co-moving transverse light clock, he will have dt′ = dt (1–v²)^1/2, so the effective length is v[(L/v)(1–v²)^1/2] = L(1–v²)^1/2. Thus, effective length contraction (and no transverse expansion) is logically unavoidable given the effective time dilation.

It might be argued that we glossed over an ambiguity in the above argument by considering only light clocks with pulses moving transversely to the motion of the mirrors, giving the relation dt′ = dt(1–v²)^1/2. If, instead, we align the axis between the mirrors with the direction of travel, we get dt′ = dt(1–v²), so it might seem we have an ambiguous measure of local time, and therefore an ambiguous prediction of length contraction since, by the reasoning given above, we would conclude that an object of rest-length L has the effective length L(1–v²). However, this fails to account for the contraction of the longitudinal distance between the mirrors (when they are arranged along the axis of motion). Since by construction the speed of light is c in terms of the local coordinates for the clock, the very same analysis that implies length contraction for objects moving relative to the ether rest frame coordinates also implies the same contraction for objects moving relative to the new local coordinates. Thus the clock is contracted in the longitudinal direction relative to the ground's coordinates by the same factor that objects on the ground are contracted in terms of the moving coordinates.

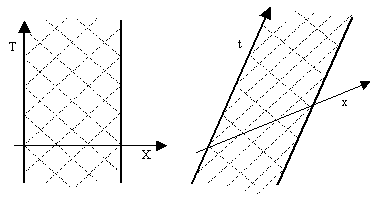
The amount of spatial contraction depends on the amount of time dilation, which depends on the amount of spatial contraction, so it might seem as if the situation is indeterminate. However, all but one of the possible combinations are logically inconsistent. For example, if we decided that the clock was shortened by the full longitudinal factor of (1–v²), then there would be no time dilation at all, but with no time dilation there would be no length contraction, so this is self-contradictory. The only self-consistent arrangement that reconciles each reference frame's local measures of longitudinal time and length is with the factor (1–v²)^1/2 applied to both. This also agrees with the transverse time dilation, so we have isotropic clocks with respect to the local (i.e., inertial) coordinates of any uniformly moving frame, and by construction the speed of light is c with respect to each of these systems of coordinates. This is illustrated by the figures below, showing how the spacetime pattern of reflecting light rays imposes a skew in both the time and the space axes of relatively moving systems of coordinates.

A slightly different approach is to notice that, according to a "transverse" light clock, we have the partial derivative ∂t/∂T = 1/(1–v²)^1/2 along the absolute time axis, i.e., the line X = 0. Integrating gives t = (T – f(X))/(1–v²)^1/2 where f(x) is an arbitrary function of X. The question is: Does there exist a function f(X) that will yield physical relativity? If such a function exists, then obviously the resulting coordinates are the ones that will be adopted as the rest frame by any observer at rest with respect to them. Such a function does indeed exist, namely, f(X) = vX, which gives t = (T–vX)/(1–v²)^1/2. To show reciprocity, note that X = vT along the t axis, so we have t = T(1–v²)/(1–v²)^1/2, which gives T = t/(1–v²)^1/2 and so ∂T/∂t = 1/(1–v²)^1/2. As we've seen, this same transformation yields relativity in the longitudinal direction as well, so there does indeed exist, for any object in any state of motion, a coordinate system with respect to which all optical phenomena are isotropic, and as a matter of empirical fact this is precisely the same class of systems invoked by Galileo's principle of mechanical relativity, the inertial systems, i.e., coordinate systems with respect to which mechanical inertia is isotropic.

Lorentz noted that the complete reciprocity and symmetry between the "true" rest frame coordinates and each of the local effective coordinate systems may seem surprising at first. As he said in his Leiden lectures in 1910

The behavior of measuring rods and clocks in translational motion, when viewed superficially, gives rise to a remarkable paradox, which on closer examination, however, vanishes.

The seeming paradox arises because the Lorentz transformation between two relatively moving systems of inertial coordinates (x,t) and (X,T) implies ∂t/∂T = ∂T/∂t, and there is a temptation to think this implies (dt)² = (dT)². This “paradox” is based on a confusion between total and partial derivatives. The parameter t is a function of both X and T, and the expression ∂t/∂T represents the partial derivative of t with respect to T at constant X. Likewise T is a function of both x and t, and the expression ∂T/∂t represents the partial derivative of T with respect to t at constant x. Needless to say, there is nothing logically inconsistent about a transformation between (x,t) and (X,T) such that (∂t/∂T)_X equals (∂T/∂t)_x, so the “paradox” (as Lorentz says) vanishes.

The writings of Lorentz and Poincare by 1905 could have been assembled into a theory of relativity that is operationally equivalent to the modern theory of special relativity, although lacking the conceptual clarity and coherence of the modern theory. Lorentz was justifiably proud of his success in developing a theory of electrodynamics that accounted for all the known phenomena, explaining the apparent relativity of these phenomena, but he was also honest enough to acknowledge that the success of his program relied on several seemingly independent hypotheses, the most significant of which was the hypothesis that inertial mass is Lorentz covariant. To place Lorentz’s achievement in context, recall that toward the end of the 19th century it appeared electromagnetism was not relativistic, because the property of being relativistic was equated with being invariant under Galilean transformations, and it was known that Maxwell’s equations (unlike Newton’s laws of mechanics) do not possess this invariance. Lorentz, prompted by experimental results, discovered that Maxwell’s equations actually are relativistic, in the sense of his theorem of corresponding states, meaning that there are relatively moving coordinate systems in terms of which Maxwell’s equations have the same form. But these systems are not related by Galilean transformations (as is easily seen by the fact that light propagates at c in any coordinate system in which Maxwell’s equations have their standard form, but there is no finite invariant speed under Galilean transformations), so it still appeared that mechanics (presumed to be Galilean covariant) and electrodynamics were not mutually relativistic, which meant it ought to be possible to discern second-order effects of absolute motion by exploiting the difference between the Galilean covariance of mechanics and Lorentz covariance of electromagnetism.

However, all experiments refuted this expectation. It was found empirically that electromagnetism and mechanics are mutually relativistic (at least to second order), so either the correct laws of electromagnetism must really be Galilean covariant, or else the correct laws of inertial mechanics must really be Lorentz covariant. At this point, in order to “save the phenomena”, Lorentz simply assumed that inertial mass is Lorentz covariant. Of course, he had before him the example of self-induction of charged objects, leading to the concept of electromagnetic mass, which is manifestly Lorentz covariant, but, as Poincare observed, in the classical context it is not possible (and doesn’t even make sense) for the intrinsic mass of elementary particles to be purely electromagnetic in origin. Hence the hypothesis of Lorentz covariance for inertia (and therefore inertial mechanics) is not a “constructive” deduction; it is not even implied by the molecular force hypothesis (because there is no reason to suppose that anything analogous to “self-induction” of the unknown molecular forces is ultimately responsible for inertia); it is simply a hypothesis, motivated by empirical facts. This does not diminish Lorentz’s achievement, but it does undercut his comment that “Einstein simply postulates what we have deduced… from the fundamental equations of the electromagnetic field”. In saying this, Lorentz overlooked the fact that the Lorentz covariance of mechanical inertia cannot be deduced from the equations of electromagnetism. He simply postulated it, no less than Einstein did. But for Lorentz it was an independent hypothesis, along with several others, and both he and Poincare failed to realize that it amounts to the hypothesis that inertial coordinate systems are related by Lorentz transformations.

Much of the confusion over whether Lorentz deduced or postulated his results is due to confusion between the two aspects of the problem. First, it was necessary to determine that Maxwell’s equations are Lorentz covariant. This was in fact deduced by Lorentz from the laws themselves, consistent with his claim. But in order to arrive at a complete theory of relativity (and in particular to account for the second-order null results) it is also necessary to determine that mechanical inertia (and molecular forces, etc.) are all Lorentz covariant. This proposition was not deduced by Lorentz (or anyone else) from the laws of electromagnetism, nor could it be, because it does not follow from those laws. It is merely postulated, just as we postulate the conservation of energy, as an organizing principle, justified by it’s logical cogency and empirical success. As Poincare clearly explained in his Palermo paper, the principle of relativity itself emerges as the only reliable guide, and this is as true for Lorentz’s approach as it is for Einstein’s, the main difference being that Einstein recognized this principle was not only necessary, but also that it obviated the detailed assumptions as to the structure of matter. Hence, even with regard to electromagnetism (let alone mechanics) Lorentz could write in the 1915 edition of his Theory of Electrons that

If I had to write the last chapter now, I should certainly have given a more prominent place to Einstein’s theory of relativity, by which the theory of electromagnetic phenomena in moving systems gains a simplicity that I had not been able to attain.

Despite this acknowledgement, Lorentz and Poincare both continued to espouse the merits of the absolute interpretation of relativity, although Poincare sometimes seemed to regard the distinction as merely conventional. For example, in a 1912 lecture he said

The new conception … according to which space and time are no longer two separate entities, but two parts of the same whole, which are so intimately bound together that they cannot be easily separated… is a new convention [that some physicists have adopted]… Not that they are constrained to do so; they feel that this new convention is more comfortable, that’s all; and those who do not share their opinion may legitimately retain the old one, to avoid disturbing their ancient habits. Between ourselves, let me say that I feel they will continue to do so for a long time still.

Sadly, Poincare died just two months later, but his prediction has held true, because to this day the “ancient habits” regarding absolute space and time persist. There are today scientists and philosophers who argue in favor of what they see as Lorentz’s constructive approach, especially as a way of explaining the appearance of relativity, rather than merely accepting relativity in the same way we accept (for example) the principle of energy conservation. However, as noted above, the constructiveness of Lorentz’s approach begins and ends with electromagnetism, the rest being conjecture and hypothesis, so this argument in favor of the Lorentzian view is misguided. But setting this aside, is there any merit in the idea that the absolutist approach effectively explains the appearance of relativity?

To answer this question, we must first clearly understand what precisely is to be “explained”. As discussed in Section 1.2, we are presented with many relativities in nature, such as the relativity of spatial orientation. It’s important to bear in mind that this relativity does not assert that the characteristic lengths of physical configurations are unaffected by orientation; it merely asserts that all such lengths are affected by orientation in exactly the same proportion. If we posit some universal anisotropy of all spatial lengths, and then note that we cannot hope to detect this anisotropy because it affects all lengths in the same proportion, so lengths will appear to be isotropic, have we thereby “explained” the apparent isotropy of spatial lengths? Not at all, we have simply explained why our hypothesis (ancient habit) of universal anisotropy has no empirical content. The empirical fact to be explained is the symmetry, i.e., why all characteristic lengths maintain exactly the same proportions, independent of their spatial orientations. Hypothesizing that this symmetry is false, but false in a special way that makes it seem true, is not very useful – except perhaps to explain why certain ancient habits were as serviceable as they were.

Similarly if we accept absolute Galilean space and time as true concepts, a priori, then it is useful to understand why nature may appear to be Minkowskian, even though it is really (by supposition) Galilean. But what is the basis for the belief in the Galilean concept of space and time, as distinct from the Minkowskian concept, especially considering that the world appears to be Minkowskian? Most physicists have concluded that there is no good answer to this question, and that it’s preferable to study the world as it appears to be, rather than trying to rationalize “ancient habits”. This does not imply a lack of interest in a deeper explanation for the effective symmetries of nature, but it does suggest that such explanations are most likely to come from studying those effective symmetries themselves, rather than from rationalizing why certain pre-conceived universal asymmetries would be undetectable.

Return to Table of Contents