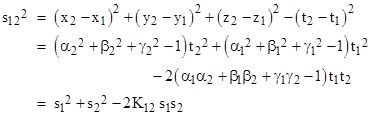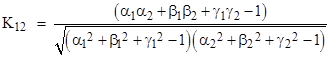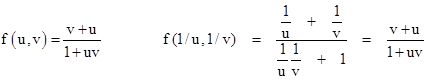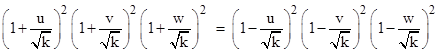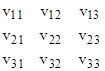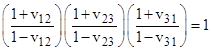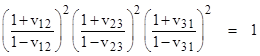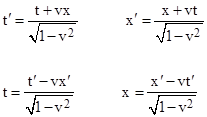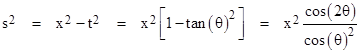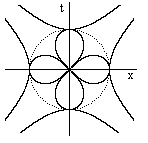1.8  More Symmetry

I cannot quite imagine it possible that any physical meaning be afforded to substitutions of reciprocal radii… It does seem to me that you are very much over-estimating the value of purely formal approaches…

                                                                                Albert Einstein to Felix Klein in 1916

We saw in previous sections that Maxwell’s equations are invariant under Lorentz transformations, as well as translations and spatial rotations. Together these transformations comprise the Poincare group. Of course, Maxwell’s equations are also invariant under spatial and temporal reflections, but it is often overlooked that in addition to all these linear transformations, Maxwell’s equations possess still another symmetry, namely, the symmetry of spacetime inversion. In a sense, an inversion is a kind of reflection about a surface in spacetime, analogous to inversions about circles in projective geometry, the only difference being that the Minkowski interval is used instead of the Euclidean line element.

Consider two events E₁ and E₂ that are null-separated from each other, meaning that the absolute Minkowski interval between them is zero in terms of an inertial coordinate system x,y,z,t. Let s₁ and s₂ denote the absolute intervals from the origin to these two events (respectively). Under an inversion of the coordinate system about the surface at an absolute interval R from the origin (which may be chosen arbitrarily), each event located on a given ray through the origin is moved to another point on that ray such that its absolute interval from the origin is changed from s to R²/s. Thus the hyperbolic surfaces outside of R are mapped to surfaces inside R, and vice versa.

To prove that two events originally separated by a null Minkowski interval are still null-separated after the coordinates have been inverted, note that the ray from the origin to the event E_j can be characterized by constants α_j, β_j, γ_j defined by

In terms of these parameters the magnitude of the interval from the origin to E_j can be written as

The squared interval between E₁ and E₂ can then be expressed as

where

Since inversion leaves each event on its respective ray, the value of K₁₂ for the inverted coordinates is the same as for the original coordinates, so the only effect on the Minkowski interval between E₁ and E₂ is to replace s₁ and s₂ with R²/s₁ and R²/s₂ respectively. Therefore, the squared Minkowski interval between the two events in terms of the inverted coordinates is

The quantity in parentheses on the right side is just the original squared interval, so if the interval was zero in terms of the original coordinates, it is zero in terms of the inverted coordinates. (More generally, the quantity s₁₂²/(s₁s₂) is invariant under spacetime inversion.) Thus inversion of a system of inertial coordinates yields a system of coordinates in which all the null intervals are preserved. It was shown in 1910 by Bateman and (independently) Cunningham that this is the necessary and sufficient condition for Maxwell’s equations to be invariant. Incidentally, Einstein was dismissive of this invariance when Felix Klein asked him about it. He wrote

I am convinced that the covariance of Maxwell’s formulas under transformation according to reciprocal radii can have no deeper significance; although this transformation retains the form of the equations, it does not uphold the correlation between coordinates and the measurement results from measuring rods and clocks.

Einstein was similarly dismissive of Minkowski’s “formal approach” to spacetime at first, but later came to appreciate the profound significance of it. In any case, it’s interesting to note that straight lines in inertial coordinate systems map to straight or hyperbolic paths under inversion. This partly accounts for the fact that, according to the Lorentz-Dirac equations of classical electrodynamics, perfect hyperbolic motion is inertial motion, in the sense that there are free-body solutions describing particles in hyperbolic motion, and a charged particle in hyperbolic motion does not radiate.

It’s also interesting that the relativistic formula for composition of two speeds is invariant under inversion of the arguments about the speed c, i.e., replacing each speed v with c²/v, which is the phase velocity of the de Broglie wave of a particle moving with speed v. Thus the composition of the velocities of two particles is the same, whether we use the particle velocities or the phase velocities of the associated matter waves. In other words, letting f(u,v) denote the composition of the (co-linear) speeds u and v, and choosing units so that c = 1, we impose the three requirements

The first two requirements are satisfied by both the Galilean and the Lorentzian composition formulas, but the third requirement is not satisfied by the Galilean formula, because that gives

However, the relativistic composition function gives

so it does comply with all three requirements. This singles out the composition law with k = 1 from the previous chapter. As indicated by Einstein’s reply to Klein, the physical significance of such ‘inversion symmetries’ is obscure. Of course, this speed inversion is not equivalent to the spacetime inversion discussed previously, but they are formally very similar. We should also note that our speed composition relationship is not symmetrical under replacement of all three speeds by their phase velocities, but only under replacement of any two of them.

To clarify this, recall that we had derived at the end of the previous chapter the relation

where u = v₁₂, v = v₂₃, and w = v₃₁. The symbol v_ij signifies the speed of the ith particle in terms of the inertial rest frame coordinates of the jth particle. With k = 0 this corresponds to the Galilean speed composition formula, which clearly is not invariant under inversion of any or all of the speeds. For any non-zero value of k, equation (1) can be re-written in the form

Squaring both sides of this equation gives the equality

If we replace each speed with its inversion in this formula, and then multiply through by (uvw)² / k³ we get

which is equivalent to the preceding formula if and only if

Hence the speed composition formula is invariant under inversion if k = ±1. The case k = –1 is equivalent to the case k = +1 if each speed is taken to be imaginary (corresponding to the use of an imaginary time axis), so without loss of generality we can choose k = +1 with real speeds. There remains, however, the ambiguity introduced by squaring both sides of equation (2), suppressing the signs of the factors. Equation (2) itself, without squaring, is invariant under inversion of any two of the speeds, but the inversion of all three speeds changes the sign of the right side. Thus by squaring both sides of (2) we make it consistent with either of the two complementary relations

The left hand relation is invariant under inversion of any two of the speeds, whereas the right hand relation is invariant under inversion of one or all three of the speeds. The question, then, is why the first formula applies rather than the second. To answer this, we should first point out that, despite the formal symmetry of the quantities u,v,w in these equations, they are not conceptually symmetrical. Two of the quantities are implicitly defined in terms of one inertial coordinate system, and the third quantity is defined in terms of a different inertial coordinate system.

In general, there are nine conceptually distinct speeds for three co-linear particles in terms of the three rest frame coordinate systems, namely

where v_ij is the speed of the ith particle in terms of the inertial rest frame coordinates of the jth particle. By definition we have v_ii = 0 and by reciprocity we have v_ij = –v_ji, so the speeds comprise an anti-symmetric array. Thus, although the three speeds v₁₂, v₂₃, v₃₁ are nominally defined in terms of three different systems of coordinates, any two of them can be expressed in terms of a single coordinate system by invoking the reciprocity relation. For example, the three quantities v₁₂, v₂₃, v₃₁ can be expressed in the form v₁₂, –v₃₂, v₃₁, which signifies that the first two speeds are both defined in terms of the rest frame coordinates of frame 2. However, the remaining speed does not have a direct expression in terms of that frame, so a composition formula is needed to relate all three quantities. We’ve seen that the relativistic composition formula yields the same value for the third speed (e.g., the speed defined in terms of frame 1) regardless of whether we use the two other speeds (e.g., the speeds defined in terms of frame 2) or their reciprocals.

To more clearly exhibit the peculiar 2+1 symmetry of this velocity composition law, note that it can be expressed in multiplicative form as

where v_ij denotes the speed of object j with respect to object i. Clearly if we replace any two of the speeds with their reciprocals, the relation remains unchanged. On the other hand, if we replace just one or all three of the speeds with their reciprocals, their product is still unity, but the sign is negated. Thus, one way of expressing the full symmetry of this relation would be to square both sides, giving the result

which is completely invariant under any replacement of one or more speeds with their respective reciprocals. Naturally we can extend the product of factors of the form (1+v_ij)/(1–v_ij) to any cyclical sequence of relative speeds between any number of co-linear points.

It’s interesting to note the progression of relations between the speeds involving one, two, and three particles. The relativity of position is expressed by the identity

for any one particle, and the relativity of velocity can be expressed by the skew symmetry

for any two systems particles. (This was referred to earlier as the reciprocity condition v_ij = –v_ji.) The next step is to consider the cyclic sum involving three particles and their respective inertial rest frame coordinate systems. This is the key relation, because all higher-order relations can be reduced to this. If acceleration were relative (like position and velocity), we would expect the cyclic symmetry v_ij + v_jk + v_ki = 0, which is a linear function of all three components. Indeed, this is the Galilean composition formula. However, since acceleration is absolute, it's to be expected that the actual relation is non-linear in each of the three components. So, instead of vanishing, we need the right side of this sum to be a symmetric function of the terms. The only other odd elementary symmetric function of three quantities is the product of all three, so we're led (again) to the relation

which can be regarded as the law of inertia. Since there is only one odd elementary symmetric function of one variable, and likewise for two variables, the case of three variables is the first for which there exists a non-tautological expression of this form.

We may also note a formal correspondence with De Morgan's law for logical statements. Letting sums denote logical ORs (unions), products denote logical ANDs (intersections), and overbars denote logical negation, De Morgan’s law states that

for any three logical variables X,Y,Z. Now, using the skew symmetry property, we can "negate" each velocity on the right hand side of the previous expression to give

From this standpoint the right hand side is analogous to the "logical negation" of the left hand side, which makes the relation analogous to setting the quantity equal to zero. The justification for regarding this relation as the source of inertia becomes more clear in Section 2.3, which describes how the relativistic composition law for velocities accounts for the increasing inertia of an accelerating object. This leads to the view that inertia itself is, in some sense, a consequence of the non-linearity of velocity compositions.

Given the composition law u′ = (u+v)/(1+uv) for co-linear speeds, what can we say about the transformation of the coordinates x and t themselves under the action of the velocity v? The composition law can be written in the form vuu′+u′–u = v, which has a natural factorization if we multiply through by v and subtract 1 from both sides, giving

If u and u′ are taken to be the spatio-temporal ratios x/t and x′/t′, the above relation can be written in the form

On the other hand, remembering that we can insert the reciprocals of any two of the quantities u, u′, v without disturbing the equality, we can take u and u′ to be the temporal-spatial ratios t/x and t′/x′ in (3) to give

These last two equations immediately give

Treating the primed and unprimed frames equivalently, and recalling that v′ = –v, we see that (4) has a perfectly symmetrical factorization, so we exploit this factorization to give the transformation equations

These are the Lorentz transformations for velocity v in the x direction. The y and z coordinates are unaffected, so we have y′ = y and z′ = z. From this it follows that the quantity t² – x² – y² – z² is invariant under a general Lorentz transformation, so we have arrived (again) at the full Minkowski spacetime metric.

For another way to depict the structure of spacetime, involving a different kind of inversion, note that for any given inertial coordinate system x,t, we can associate with each event an angle θ defined by tan(θ) = t/x. Thus the interval from the origin to the point x,t makes an angle θ with the positive x axis, and we have t = x tan(θ), so we can express the squared magnitude of a spacelike interval as

Multiplying through by cos(θ)² gives

Substituting t²/tan(θ)² for x² gives the analogous expression

Adding these two expressions gives the result

Consequently the "circular" locus of events satisfying x² + t² = r² for any fixed r can be represented in polar coordinates (s,θ) by the equation

which is the equation of two lemniscates, represented by the two perpendicular “infinity symbols” in the figure below (with real spacelike and imaginary timelike values of s).

The lemniscate was first discussed by Jakob Bernoulli in 1694, as the locus of points satisfying the equation

which is, in Bernoulli's words, "a lying eight-like figure, folded in a knot of a bundle, or of a lemniscus, a knot of a French ribbon". (The study of this curve led Fagnano, Euler, Legendre, Gauss, and others to the discovery of addition theorems for integrals, of which the relativistic velocity composition law is an example.) Notice that the lemniscate is the inverse (in the sense of inversive geometry) of the hyperbola relative to the circle of radius k. In other words, if we draw a line emanating from the origin and it strikes the lemniscate at the radius s, then it strikes the hyperbola at the radius R where sR = k². This follows from the fact that the equation for a hyperbola in polar coordinates is R² = k²/[ε² cos(θ)² - 1] where ε is the eccentricity, and for an orthogonal hyperbola we have ε =. Hence the denominator is 2cos(θ)² – 1 = cos(2θ), and the equation of the hyperbola is R² = k²/cos(2θ). Since the polar equation for the lemniscate is s² = k²cos(2θ) we have sR = k².

Return to Table of Contents