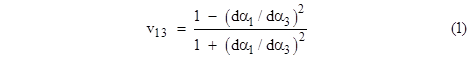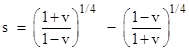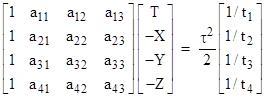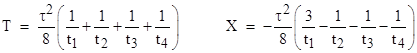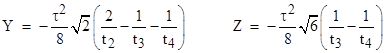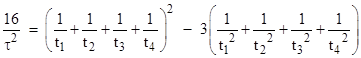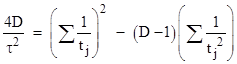1.9 Null Coordinates

Slight not what’s near through aiming at what’s far.

Euripides, 455 BC

Initially the special theory of relativity was regarded by many as just a particularly simple and elegant interpretation of Lorentz's ether theory, but it gradually became clear that there is a profound difference between the two theories, most evident when we consider the singularity implicit in the Lorentz transformation x' = γ(x−vt), t' = γ(t−vx), where γ = 1/(1−v²)^1/2. As v approaches arbitrarily close to 1, the factor γ goes to infinity. If these relations are strictly valid (locally), as all our observations and experiments suggest, then according to Lorentz's view all configurations of objects moving through the absolute ether must be capable of infinite spatial "contractions" and temporal "dilations", without the slightest distortion. This is inconsistent with a particulate substantial ether (a genuine continuum would have its own difficulties), so a Lorentzian must believe that the Lorentz transformation equations are not strictly valid, i.e., that they break down at some point. Indeed, Lorentz himself argued that his view was preferable precisely because absolute speed might eventually be found to make some difference to the intrinsic relations between physical entities. However, one hundred years after Lorentz's time, there still is no sign of any such difference. To the contrary, all tests of local Lorentz invariance have consistently confirmed it's precise validity – even at the most extreme conditions. If the Lorentz transformation really is exactly correct, the Lorentzian approach has the wrong topology, analogous to trying to define a continuous map from the surface of a sphere to a flat plane: stereographic projection can provide a nearly complete mapping, but we need to map the “north pole” of the sphere to a point at infinity. This shows that the surface of a sphere is the more natural representation of the topology. Likewise the null intervals of special relativity signal that the topology of spacetime is actually the one induced by the Minkowski interval, rather than supposing a contorted version of the Euclidean topology of Lorentz’s ether. (Section 9 discusses the implications of this relativistic topology for our ideas of causality.) It is also worth recalling from the previous section that the necessary and sufficient condition for Maxwell’s equations to be invariant under a given transformation is that the null intervals are preserved.

The singularity of the Lorentz transformation is most clearly expressed in terms of the underlying Minkowski pseudo-metric. Recall that the invariant space time interval dτ between the events (t,x) and (t+dt, x+dx) is given by

where t and x are any set of inertial coordinates. This is called a pseudo-metric rather than a metric because, unlike a true metric, it doesn't satisfy the triangle inequality, and the interval between distinct points can be zero. This occurs for any interval such that dt = dx, in which case the invariant interval dt is literally zero. It’s worth noting that quantum field theory is possible only in the context of Minkowski spacetime, with its null connections between distinct events, as discussed in Section 9.10.

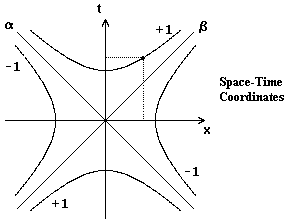
Pictorially, the locus of points whose squared distance from the origin is ±1 consists of the two hyperbolas labeled +1 and −1 in the figure below.

The diagonal axes denoted by α and β represent the paths of light through the origin, and the magnitude of the squared spacetime interval along these axes is 0, i.e., the metric is degenerate along those lines. 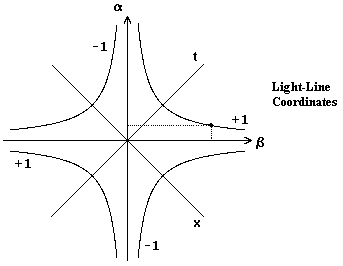This is all expressed in terms of conventional space and time coordinates, but it's also possible to define the spacetime separations between events in terms of null coordinates along the light-line axes. Conceptually, we rotate the above figure by 45 degrees, and regard the α and β lines as our coordinate axes, as shown below:

In terms of a linear parameterization α = (t+x)λ, β = (t−x)/λ of these "null coordinates" for any constant λ, the locus of points at a squared "distance" (dτ)² from the origin is an orthogonal hyperbola satisfying the equation

Since the light-lines α and β are degenerate, in the sense that the absolute spacetime intervals along those lines vanish, the absolute velocity of a worldline, given by the "slope" dβ/dα = 0/0, is strictly undefined. This indeterminacy, arising from the singular null intervals in spacetime, is at the heart of special relativity, allowing for infinitely many different scalings of the light-line coordinates. In particular, it is natural to define the rest frame coordinates α,β of any worldline in such a way that dα/dβ = 1. This expresses the principle of relativity, and also entails Einstein's second principle, i.e., that the (local) velocity of light with respect to the natural measures of space and time for any worldline is unity. The relationship between the natural null coordinates of any two worldlines is then expressed by the requirement that, for any given interval dτ, the components dα,dβ with respect to one frame are related to the components dα',dβ' with respect to another frame according to the equation (dα)(dβ) = (dα')(dβ'). It follows that the scale factors of any two frames S_i and S_j are related according to

where v_ij is the usual velocity parameter (in units such that c = 1) of the origin of S_j with respect to S_i. Notice there is no absolute constraint on the scaling of the α and β axes, there is only a relative constraint, so the "gage" of the light-lines really is indeterminate. Also, the scale factors are simply the relativistic Doppler shifts for approaching and receding sources (see Section 2.4). This accords with the view of the αβ coordinate "grid lines" as the network of light-lines emitted by a strobed source moving along the reference world-line.

To illustrate how we can operate with these null coordinate scale relations, let us derive (again) the addition rule for velocities. Given three co-linear unaccelerated particles with the pairwise relative velocity parameters v₁₂, v₂₃, and v₁₃, we can solve the "α scale" relation for v₁₃ to give

We also have

Multiplying these together gives an expression for dα₁/dα₃, which can be substituted into (1) to give the expected result

Interestingly, although neither the velocity parameter v nor the quantity (1+v)/(1−v) is additive, it's easy to see that the parameter ln[(1+v)/(1−v)] is additive. In fact, this parameter corresponds to the invariant arc length of the "τ = constant" hyperbola connecting the two world lines at unit distances from their intersection (taken to be at the origin), as shown by integrating the differential distance along that curve

Since the equation of the unit hyperbola is t² − x² = 1 we have

Substituting this into the previous expression and performing the integration gives

Since v = x/t, and noting that t² − x² = 1 implies t + x = 1 / (t − x), it follows that the quantity x + t can be written as

Hence the absolute arc length along the τ = 1 surface between two world lines that intersect at the origin with a mutual velocity v is

This shows that the arc length s is identical to the angle θ in the expression of the Lorentz transformation as a hyperbolic rotation, discussed in Section 1.7. Naturally the additivity of this logarithmic form implies that the argument is a multiplicative measure of mutual speeds. Incidentally, the absolute interval between the intersection points of the two worldlines with the dτ = 1 hyperbola can be written as

One strength of the conventional pseudo-metrical formalism is that (t,x) coordinates easily generalize to (t,x,y,z) coordinates, and the invariant interval generalizes to

The generalization of the null (lightlike) coordinates and corresponding invariant is not as algebraically straightforward, but it conveys some interesting aspects of the spacetime structure. Intuitively, an observer can conceive of the absolute interval between himself and some distant future event P by first establishing a scale of radial measure outward on his forward light cone in all directions, and then for each direction evaluate the parameterized null measure along the light cone to the point of intersection with the backward null cone of P. This will assign, to each direction in space, a parameterized distance from the observer to the backward light cone of P, and there will be (in flat spacetime) two distinguished directions, along which the null measure is maximum or minimum. These are the principle directions for the interval from the observer to E, and the product of the null measures in these directions is invariant. In other words, if a second observer, momentarily coincident with the first but with some relative velocity, determines the null measures along the principle directions to the backward light cone of E, with respect to his own natural parameterization, the product will be the same as found by the first observer.

It's often convenient to take the interval to the point P as the time axis of inertial coordinates t,x,y,z, so the eigenvectors of the null cone intersections become singular, and we can simply define the null coordinates u = t + r, v = t − r, where r = (x²+y²+z²)^1/2. From this we have t = (u+r)/2 and r = (u−v)/2 along with the corresponding differentials dt = (du+dv)/2 and dr = (du−dv)/2. Making these substitutions into the usual Minkowski metric in terms of polar coordinates

we have the Minkowski line element in terms of angles and null coordinates

These coordinates are often useful, but we can establish a more generic system of null coordinates in 3+1 dimensional spacetime by arbitrarily choosing four non-parallel directions in space from an observer at O, and then the coordinates of any timelike separated event are expressed as the four null measures radially in those directions along the forward null cone of O to the backward null cone of P. This provides enough information to fully specify the interval OP.

We can specify the ordinary orthogonal coordinates (T,X,Y,Z) of event P relative to the observer O at the origin in terms of the coordinates of four events I₁, I₂, I₃, I₄ on the intersection of the forward null cone of O and the backward null cone of P. If t_i,x_i,y_i,z_i denote the ordinary coordinates of I_i, then we have

for i = 1, 2, 3, 4. Expanding the right hand equations and canceling based on the left hand equalities, we have the system of equations

The left hand side of all four of these equations is the invariant squared proper time interval τ² from O to P, and we wish to express this in terms of just the four null measures in the four chosen directions. For a specified set of directions in space, this information can be conveyed by the four values t₁, t₂, t₃, and t₄, since the magnitudes of the spatial components are determined by the directions of the axes and the magnitude of the corresponding t. In general we can define the direction coefficients a_ij such that

with the condition a_i1² + a_i2² + a_i3² = 1. Making these substitutions, the system of equations can be written in matrix form as

We can use any four directions for which the determinant of the coefficient matrix does not vanish. One natural choice is to use the vertices of a regular tetrahedron inscribed in a unit sphere, so that the four directions are perfectly symmetrical. We can take as the coordinates of the vertices

Inserting these values for the direction coefficients a_ij, we can solve the matrix equation for T, X, Y, and Z to give

Substituting into the relation τ² = T² − X² − Y² − Z² and solving for τ² gives

Naturally if t₁ = t₂ = t₃ = t₄ = t, then this gives τ = ±2t. This expression is perfectly symmetrical in the four lightlike coordinates, but it applies only for coordinates in which the null rays are directionally symmetrical, so it is not an invariant expression because aberration alters the relative ray angles under a Lorentz transformation.

More generally, in a spacetime of 1 + (D−1) dimensions, the invariant interval in terms of D directionally symmetrical null measures t₁, t₂,..., t_D satisfies the equation

It can be verified that with D = 2 this expression reduces to τ² = 4t₁t₂ , which agrees with our earlier expression τ² = αβ with α = 2t₁ and β=2t₂. If we define u_j = 1/t_j , this equation can be written in the form

where σ is the average squared difference of the individual u terms from the average, i.e.,

Were is not for the variance term, the squared proper time (to the midpoint of the interval) would be just the harmonic mean of the coordinate times.

The product form s² = αβ for the invariant interval s² = x² − t² is reminiscent of other fundamental relations of physics that have found expression as hyperbolic relations, such as the uncertainty relation

in quantum mechanics, where h is Planck's constant. We can draw an analogy between these uncertainty relations of maximally incompatible variables and the product form of the invariant line element (of a given interval) in terms of the variables parameterizing two oppositely directed null rays in spacetime. For the quantum uncertainty relation, we can choose a basis of evaluation of a given particle that makes the variance of either the position or the momentum arbitrarily small, but then the minimal variance of the other is correspondingly large, such that the product is unchanged. Likewise for a given spacetime interval we can choose a basis of evaluation that makes either of the null ray parameters arbitrarily small, but then the other is correspondingly large, such that the product is unchanged.

In both cases we have two variables, either position and momentum or the two lightlike null ray parameters (along the eigenvectors of the Lorentz transformation), that vary as a function of the chosen basis of evaluation (system of reference), but they vary in a way that leaves their minimal product unchanged.

In quantum mechanics one might imagine that a particle possesses a precise position and momentum but we are unable to determine these due to practical limitations (disturbances) of our measurement techniques. From that point of view, it might seem that if only we had infinitely weak signals, i.e., if only h = 0, we could determine both position and momentum with infinite precision. Likewise in special relativity one might imagine that there is an absolute simultaneity between the times of two distant locations, but that we are prevented from determining it due to the practical limitations (time delays) of our measurement devices. It might seem that if only we had infinitely fast signals, i.e., if only 1/c was zero, we could determine absolute simultaneity. In both cases the premise is that nature possesses structure and information that happens to be inaccessible to us (i.e., hidden variables) due to the limitations of our measuring capabilities.

However, a more natural interpretation is that the limitations imposed by quantum mechanics (h ≠ 0) and special relativity (1/c ≠ 0) are not limitations of measurement, but expressions of an actual ambiguity and "incompatibility" in the independent meanings of those variables. One of Einstein's main contributions to modern relativity was the idea that there is no one "true" simultaneity between spatially separate events, but rather spacetime events are only partially ordered, and the decomposition of space and time into separate variables contains an inherent ambiguity on the scale of 1/c. In other words, he rejected what we might call Lorentz's "hidden variable" approach, and insisted on treating the ambiguity in the spacetime decomposition as fundamental. This is interesting in part because, when it came to quantum mechanics, Einstein's instinct was to continue trying to find ways of measuring the "hidden variables", and he was never comfortable with the idea that the Heisenberg uncertainty relations express a fundamental ambiguity in the decomposition of conjugate variables on the scale of h. In 1926, Heisenberg responded to Einstein’s skepticism by pointing out that Einstein himself had taken similarly positivistic ideas as the basis of his special theory of relativity, to which Einstein replied "Perhaps I did use such philosophy earlier, and also wrote of it, but it is nonsense all the same." He argued that there are no theory-free observations. The theory first determines what can be observed.

Return to Table of Contents