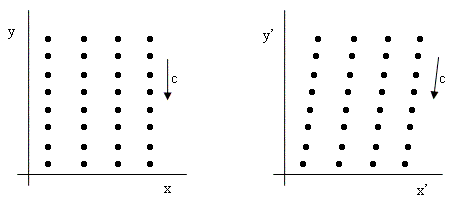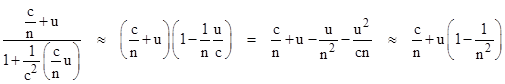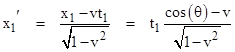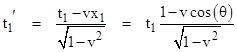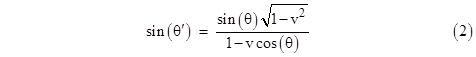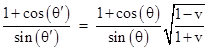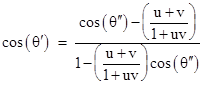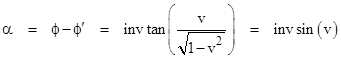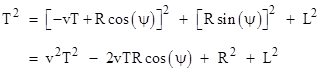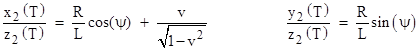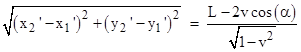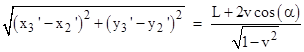2.5  Stellar Aberration

It was chiefly therefore Curiosity that tempted me (being then at Kew, where the Instrument was fixed) to prepare for observing the Star on December 17th, when having adjusted the Instrument as usual, I perceived that it passed a little more Southerly this Day than when it was observed before.

                                                                  James Bradley, 1727

The aberration of starlight was discovered in 1727 by the astronomer James Bradley while he was searching for evidence of stellar parallax, which in principle ought to be observable if the Copernican theory of the solar system is correct. He succeeded in detecting an annual variation in the apparent positions of stars, but the variation was not consistent with parallax. The observed displacement was greatest for stars in the direction perpendicular to the orbital plane of the Earth, and most puzzling was the fact that the displacement was exactly three months (i.e., 90 degrees) out of phase with the effect that would result from parallax due to the annual change in the Earth’s position in orbit around the Sun. It was as if he was expecting a sine function, but found instead a cosine function. Now, the cosine is the derivative of the sine, so this suggests that the effect he was seeing was not due to changes in the earth’s position, but to changes in the Earth’s (directional) velocity. Indeed Bradley was able to interpret the observed shift in the incident angle of starlight relative to the Earth’s frame of reference as being due to the transverse velocity of the Earth relative to the incoming corpuscles of light, assuming the latter to be moving with a finite speed c. The velocity of the corpuscles relative to the Earth equals their velocity vector c with respect to the Sun’s frame of reference plus the negative of the orbital velocity vector v of the Earth, as shown below.

In this figure, θ₁ is the apparent elevation of a star above the Earth’s orbital plane when the Earth’s velocity is most directly toward the star (say, in January), and θ₂ is the apparent elevation six months later when the Earth’s velocity is in the opposite direction. The law of sines gives

For the special case of a star located exactly perpendicular to the Earth’s orbital plane, we have sin(θ) = cos(α), so Bradley’s formula gives tan(α) = v/c. In general, since the aberration angles α are quite small, we can closely approximate sin(α) with just α, so the apparent position of a star that is roughly θ above the ecliptic ought to describe a small circle (or ellipse) around its true position, and the “radius” of this path should be sin(θ)(v/c) where v is the Earth’s orbital speed and c is the speed of light. When Bradley made his discovery he was examining the star γ Draconis, which has a declination of about 51.5 degrees above the Earth’s equatorial plane, and about 75 degrees above the ecliptic plane. Incidentally, most historical accounts say Bradley chose this star simply because it passes directly overhead in Greenwich England, the site of his observatory, which happens to be at about 51.5 degrees latitude. Vertical observations minimize the effects of atmospheric refraction, but surely this is an incomplete explanation for choosing γ Draconis, because stars with this same declination range from 28 to 75 degrees above the ecliptic, due to the Earth’s tilt of 23.5 degrees. Was it just a lucky coincidence that he chose (as Leibniz had previously) γ Draconis, a star with the maximum possible elevation above the ecliptic among stars that pass directly over Greenwich? Accidental or not, he focused on nearly the ideal star for detecting aberration. The orbital speed of the Earth is roughly v = (2.98)10⁴ m/sec, and the speed of light is c = (3.0)10⁸ m/sec, so the magnitude of the aberration for γ Draconis is (v/c)sin(75 deg) = (9.59)10^-5 radians = 19.8 seconds of arc. Bradley subsequently confirmed the expected aberration for stars at other declinations.

Ironically, although it was not the effect Bradley had been seeking, the existence of stellar aberration was, after all, conclusive observational proof of the Earth’s motion, and hence of the Copernican theory, which had been his underlying objective. Furthermore, the discovery of stellar aberration not only provided the first empirical proof of the Copernican theory, it also furnished a new and independent proof of the finite speed of light, and even enabled that speed to be estimated from knowledge of the orbital speed of the Earth. The result was consistent with the earlier estimate of the speed of light by Roemer based on observations of Jupiter’s moons (see Section 3.3).

Bradley’s interpretation, based on the Newtonian corpuscular concept of light, accounted quite well for the basic phenomenon of stellar aberration, but it requires us to believe that the velocity of light is remarkably constant from all sources in all circumstances. Indeed, commenting on the concordance between the speed of light inferred from aberration and from Roemer’s method based on the Sun’s light reflected from Jupiter’s moons, Bradley wrote

These different Methods of finding the Velocity of Light thus agreeing, we may reasonably conclude, not only that these Phaenomena are owing to the Causes to which they have been ascribed; but also, that Light is propagated (in the same Medium) with the same Velocity after it hath been reflected as before; for this will be the Consequence, if we allow that the Light of the Sun is propagated with the same Velocity, before it is reflected, as the Light of the fixt Stars. And I imagine this will scarce be questioned, if it can be made appear that the Velocity of the Light of all the fixt Stars is equal, and that their Light moves or is propagated through equal Spaces in equal Times, at all Distances from them: both which points (as I apprehend) are sufficiently proved from the apparent alteration of the Declination of Stars of different Lustre; for that is not sensibly different in such Stars as seem near together, though they appear of very different Magnitudes. And whatever their Situations are, I find the same Velocity of Light from my Observations of small Stars of the fifth or sixth, as from those of the second and third Magnitude, which in all Probability are placed at very different Distances from us.

It’s interesting that Bradley here refers to light propagating in a medium, whereas in his explanation of aberration he referred to “particles of light”, suggesting some kind of ballistic theory. However, if light consists of ballistic corpuscles their speeds ought to depend on the relative motion between the source and observer, and these differences in speed ought to be detectable, whereas no such differences were found. For example, early in the 19^th century Arago compared the focal length of light from a particular star at six-month intervals, when the Earth’s motion should alternately add and subtract a velocity component equal to the Earth’s orbital speed to the speed of light. According to the corpuscle theory, this should result in a slightly different focal length through the system of lenses, but Arago observed no difference at all. In another experiment he viewed the aberration of starlight through a normal lens and through a thick prism with a very different index of refraction, which ought to give a slightly different aberration angle according to the Newtonian corpuscular model, but he found no difference. Both these experiments suggest that the speed of light is independent of the motion of the source, so they tended to support the wave theory of light, rather than the corpuscular theory.

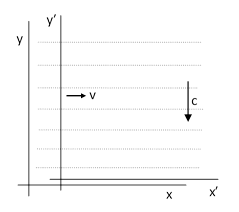
Unfortunately, the phenomenon of stellar aberration is somewhat problematic for theories that regard electromagnetic radiation as waves propagating in a luminiferous ether. It’s worthwhile to examine the situation in some detail, because it is a nice illustration of the clash between mechanical and electromagnetic phenomena within the context of Galilean relativity. If we conceive of the light emanating from a distant star reaching the Earth’s location as a set of essentially parallel streams of particles normal to the Earth’s orbit (as Bradley did), then we have the situation shown in the left-hand figure below, and if we apply the Galilean transformation to a system of coordinates moving with the Earth (in the positive x direction) we get the situation shown in the right-hand figure.

According to this model the aberration arises because each corpuscle has equations of motion of the form y = −ct and x = x₀, so the Galilean transformation x = xʹ+vt, y = yʹ, t = tʹ leads to yʹ = −ctʹ and xʹ+vt = x₀, which gives (after eliminating t) the path xʹ – v(yʹ/c) = x₀. Thus we have dxʹ/dyʹ = v/c = tan(α). In contrast, if we conceive of the light as essentially a plane wave, the sequence of wave crests is as shown below.

In this case each wavecrest has the equation y = −ct, with no x specification, because the wave is uniform over the entire wavefront. Applying the same Galilean transformation as before, we get simply yʹ = −ctʹ, so the plane wave looks the same in terms of both systems of coordinates. We might try to argue that the flow of energy follows definite streamlines, and if these streamlines are vertical with respect to the unprimed coordinates they would transform into slanted streamlines in the primed coordinates, but this would imply that the direction of propagation of the wave energy is not exactly normal to the wave fronts, in conflict with Maxwell’s equations. This highlights the incompatibility between Maxwell’s equations and Galilean relativity, because if we regard the primed coordinates as stationary and the distant star as moving transversely with speed –v, then the waves reaching the Earth at this moment should have the same form as if they were emitted from the star when it was to the right of its current position, and therefore the wave fronts ought to be slanted by an angle of v/c. Of course, we do actually observe aberration of this amount, so the wave fronts really must be tilted with respect to the primed coordinates, and we can fairly easily explain this in terms of the wave model, but the explanation leads to a new complication.

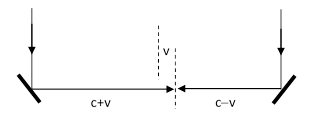
According to the early 19th century wave model with a stationary ether, an observation of a distant star consists of focusing a set of parallel rays from that star down to a point, and this necessarily involves some propagation of light in the transverse direction (in order to bring the incoming rays together). Taking the focal point to be midway between two rays, and assuming the light propagates transversely at the same speed in both directions, we will align our optical device normal to the plane wave fronts. However, suppose the effective speed of light is slightly different in the two transverse directions. If that were the case, we would need to tilt our optical device, and this would introduce a time skew in our evaluation of the wave front, because our optical image would associate rays from different points on the wave front at slightly different times. As a result, what we regard as the wave front would actually be slanted. The proponents of the wave model argued that the speed of light is indeed different in the two transverse directions relative to a telescope on the Earth pointed up at a star, because the Earth is moving sideways (through the ether) with respect to the incoming rays. Assuming light always propagates at the fixed speed c relative to the ether, and assuming the Earth is moving at a speed v relative to the ether, we could argue that the transverse speed of light inside our telescope is c+v in one direction and c−v in the other. To assess the effect of this asymmetry, consider for simplicity just two mirror elements of a reflecting telescope, focusing incoming rays as illustrated below.

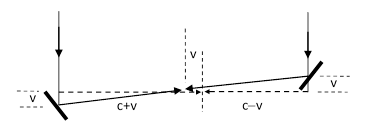
The two incoming rays shown in this figure are from the same wavecrest, but they are not brought into focus at the midpoint of the telescope, due to the (putative) fact that the telescope is moving sideways through the ether with a speed v. Both pulses strike the mirrors at the same time, but the left hand pulse goes a distance proportional to c+v in the time it takes the right hand pulse to go a distance proportional to c−v. In order to bring the wave crest into focus, we need to increase the path length of the left hand ray by a distance proportional to v, and decrease the right hand path length by the same distance. This is done by tilting the telescope through a small angle whose tangent is roughly v/c, as shown below.

Thus the apparent optical wavefront is tilted by an angle θ given by tan(θ) = v/c, which is the same as the aberration angle for the rays, and also in agreement with the corpuscle model. However, this simple explanation assumes a total vacuum, and it raises questions about what would happen if the telescope was filled with some material medium such as air or water. It was already accepted in Fresnel’s day, for both the wave and the corpuscle models of light, that light propagates more slowly in a dense medium than in vacuum. Specifically, the speed of light in a medium with index of refraction n is c/n. Hence if we fill our reflecting telescope with such a medium, then the speed of light in the two transverse directions would be c/n + v and c/n – v, and the above analysis would lead us to expect an aberration angle given by tan(θ) = nv/c. The index of refraction of air is just 1.0003, so this doesn’t significantly affect the observed aberration angle for telescopes in air. However, the index of refraction of water is 1.33, so if we fill a telescope with water, we ought to observe (according to this theory) significantly more stellar aberration. Such experiments have actually been carried out, but no effect on the aberration angle is observed.

In 1818 Fresnel suggested a way around this problem. His hypothesis, which he admitted appeared extraordinary at first sight, was that although the luminiferous ether through which light propagates is nearly immobile, it is dragged along slightly by material objects, and the higher the refractive index of the object, the more it drags the ether along with its motion. If an object with refractive index n moves with speed v relative to the nominal rest frame of the ether, Fresnel hypothesized that the ether inside the object is dragged forward at a speed (1 – 1/n²)v. Thus for objects with n = 1 there is no dragging at all, but for n greater than 1 the ether is pulled along slightly. Fresnel gave a plausibility argument based on the relation between density and refractivity, making his hypothesis seem at least slightly less contrived, although it was soon pointed out that since the index of refraction of a given medium varies with frequency, Fresnel’s model evidently requires a different ether for each frequency. Neglecting this second-order effect of chromatic dispersion, Fresnel was able on the basis of his partial dragging hypothesis to account for the absence of any change in stellar aberration for different media. He pointed out that, in the above analysis, the speed of light in the two directions has the values

For the vacuum we have n = 1, and these expressions are the same as before. In the presence of a material medium with n greater than 1, the optical device must now be tilted through an angle whose tangent is approximately

It might seem as if Fresnel’s hypothesis has simply resulted in exchanging one problem for another, but recall that our telescope is aligned normal to the apparent wave front, whereas it is at an angle of v/c to the normal of the actual wave front, so the wave will be refracted slightly (assuming n is not equal to 1). According to Snell’s law (which for small angles is n₁θ₁ = n₂θ₂), the refracted angle will be less than the incident angle by the factor 1/n. Hence we must orient our telescope at an angle of v/c in order for the rays within the medium to be at the required angle.

This is how, on the basis of somewhat adventuresome hypotheses and assumptions, physicists of the 19th century were able to reconcile stellar aberration with the wave model of light. (Accommodating the lack of effect of differing indices of refraction proved to be even more challenging for the corpuscular model.) Fresnel’s remarkable hypothesis was directly confirmed (many years later) by Fizeau, and it is now recognized as a first-order approximation of the relativistic velocity addition law, composing the speed of light in a medium with the speed of the medium

It’s worth noting that all the “speeds” discussed here are phase speeds, corresponding to the time parameter for a given wave. Lorentz later showed that Fresnel’s formula could also be interpreted in the context of a perfectly immobile ether along with the assumption of phase shifts in the incoming wave fronts so that the effective time parameter transformation was not the Galilean tʹ = t but rather tʹ = t – vx/c².

Despite the success of Fresnel’s hypothesis in matching all optical observations to the first order in v/c, many physicists considered his partially dragged ether model to be ad hoc and unphysical (especially the apparent need for a different ether for each frequency of light), so they sought other explanations for stellar aberration that would be consistent with a more mechanistically realistic wave model. As an alternative to Fresnel’s hypothesis, Lorentz evaluated a proposal of Stokes, who in 1846 had suggested that the ether is totally dragged along by material bodies (so the ether is co-moving with the body at the body’s surface), and is irrotational, incompressible, and inviscid, so that it supports a velocity potential. Under these assumptions it can be shown that the normal of a light wave incident on the Earth undergoes a total deflection during its approach such that (to first order) the apparent shift in the star’s position agrees with observation. Unfortunately, as Lorentz pointed out, the assumptions of Stokes’ theory are mutually contradictory, because the potential flow field around a sphere does not give zero velocity on the sphere’s surface. Instead, the velocity of the ether wind on the Earth’s surface would vary with position, and so too would the aberration of starlight. Planck suggested a way around this objection by supposing the luminiferous ether was compressible, and accumulated with greatly increased density around large objects. Lorentz admitted that this was conceivable, but only if we also assume the speed of light propagating through the ether is unaffected by the changes in density of the ether, an assumption that plainly contradicts the behavior of wave propagation in ordinary substances. He concluded

In this branch of physics, in which we can make no progress without some hypothesis that looks somewhat startling at first sight, we must be careful not to rashly reject a new idea… yet I dare say that this assumption of an enormously condensed ether, combined, as it must be, with the hypothesis that the velocity of light is not in the least altered by it, is not very satisfactory.

With the failure of Stokes’ theory, the only known way of reconciling stellar aberration with a wave theory of light was Fresnel’s “extraordinary” hypothesis of partial dragging, or Lorentz’s equivalent interpretation in terms of the effective phase time parameter tʹ. However, the Fresnel-Lorentz theory predicted a non-null result for the Michelson-Morley experiment, which was the first experiment accurate to the second order in v/c. To remedy this, Lorentz ultimately incorporated Fitzgerald’s length contraction into his theory, which amounts to replacing the Galilean transformation xʹ = x − vt with the relation xʹ = (x – vt)/ (1 – (v/c)²)^1/2, and then for consistency applying this same second-order correction to the time transformation, giving tʹ = (t – vx/c²)/(1 – (v/c)²)^1/2, thereby arriving at the full Lorentz transformation. By this point the posited luminiferous ether had lost all of its mechanistic properties.

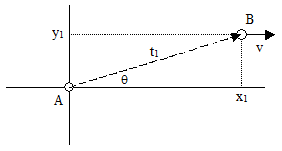
Meanwhile, Einstein's 1905 paper on the electrodynamics of moving bodies included a greatly simplified derivation of the full Lorentz transformation, dispensing with the ether altogether, and analyzing a variety of phenomena, including aberration, from a purely kinematical point of view. All the difficulties and ambiguities in the prior attempts to explain aberration instantly vanished. If a pulse of light is emitted from object A at the origin of the xyt coordinates (note that A need not be at rest in terms of these coordinates), and if the path of the light pulse makes an angle θ relative to the x axis in terms of these coordinates, then at time t₁ it will have reached the point

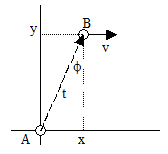
(The units have been scaled to make c = 1, so the Minkowski metric for a null interval gives x₁² + y₁² = t₁².) Now consider an object B moving in the positive x direction with velocity v, and being struck by the photon at time t₁ as shown below.

Naturally an observer riding along with B will not see the light ray arriving at an angle θ from the x axis, because in terms of the inertial rest frame coordinates of B the x axis is contracted whereas the y axis is not. Since the angle is just the arctangent of the ratio of Δy to Δx of the photon's path, and since value of Δx is different with respect to B's co-moving inertial coordinates whereas Δy is the same, it's clear that the angle of the photon's path is different with respect to B's co-moving coordinates than with respect to the original xyt coordinates. Thus aberration is simply a consequence of the kinematic transformation of angles from one system of inertial coordinates to another.

To determine the angle of the incoming ray with respect to the co-moving inertial coordinates of B, let xʹyʹtʹ be an orthogonal coordinate system aligned with the xyt coordinates but moving in the positive x direction with velocity v, so that B is at rest in the primed coordinate system. Without loss of generality we can co-locate the origins of the primed and unprimed coordinate systems, so in both systems the photon is emitted at (0,0,0). The endpoint of the photon's path in the primed coordinates can be computed from the unprimed coordinates using the standard Lorentz transformation for a boost in the positive x direction:

Just as we have cos(θ) = x₁/t₁, we also have cos(θ') = x₁ʹ/t₁ʹ, and so

which is the general relativistic aberration formula relating the angles of light rays with respect to relatively moving coordinate systems. Likewise we have sin(θʹ) = y₁ʹ/t₁ʹ, from which we get

Using these expressions for the sine and cosine of θʹ it follows that

Recalling the trigonometric identity tan(z) = sin(2z)/[1+cos(2z)] this gives

which immediately shows that aberration can be represented by stereographic projection from a sphere to the tangent plane. (This is discussed more fully in Section 2.6.)

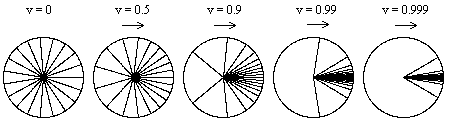
To see the effect of equation (3), suppose that, with respect to the inertial rest frame of a given particle, the rays of starlight incident on the particle are uniformly distributed in all directions. Then suppose the particle is given some speed v in the positive x direction relative to this original isotropic frame, and we evaluate the angles of incidence of those same rays of starlight with respect to the particle's new rest frame. The results, for speeds ranging from 0 to 0.999, are shown in the figure below. (Note that the angles in equation (3) are evaluated between the positive x or x' axis and the positive direction of the light ray.)

In the preceding discussion we considered light emitted from A, at rest in the unprimed coordinates, and received at B, at rest in the primed coordinate system, which is moving relative to the unprimed system. We could just as well consider light emitted from B and received at A, repeating the above derivation, except that the direction of the light ray is reversed, going now from B to A. The spatial coordinates are all the same but the emission event now occurs at −t₁, because it is in the past of event (0,0,0). The result is simply to replace each occurrence of v in the above expressions with −v. Of course, we could reach the same result simply by transposing the primed and unprimed angles in the above expressions.

Incidentally, the aberration formula used by astronomers to evaluate the shift in the apparent positions of stars resulting from the Earth's orbital motion is often expressed in terms of angles with respect to the y axis, i.e., the axis perpendicular to the relative velocity, as shown below.

This configuration corresponds to a distant star at A sending starlight to the Earth at B, which is moving nearly perpendicular to the incoming ray, so the star is far from the ecliptic plane. Aberration is greatest when α is near zero. The aberration formulas in terms of ϕ can be found simply by substituting sin(ϕ) and cos(ϕ) for cos(θ) and sin(θ) respectively (and likewise for the primed angles) in equations (1) and (2), leading to the results

For example, in the perpendicular case ϕʹ = 0 we see from the left hand equation that sin(ϕ) = v, so the aberration angle α = ϕ − ϕʹ satisfies sin(α) = v, which differs from Bradley’s formula tan(α) = v for this case, but the difference is appreciable only for large v.

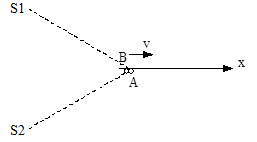
Another interesting aspect of aberration is illustrated by considering two separate light sources S₁ and S₂, and two momentarily coincident observers A and B as shown below

If observer A is stationary with respect to the sources of light, he will see the incoming rays of light striking him from the negative x direction. Thus, the light will impart a small amount of momentum to observer A in the positive x direction. On the other hand, suppose observer B is moving to the right (away from the sources of light) at nearly the speed of light. According to our aberration formula, if B is traveling with a sufficiently great speed, he will see the light from S₁ and S₂ approaching from the positive x direction, which means that the photons are imparting momentum to B in the negative x direction − even though the light sources are "behind" B in terms of the rest frame coordinates of A. This may seem paradoxical, but the explanation becomes clear when we realize that the x component of the velocities of the incoming light rays is less than c (because (vx)² = c² − (vy)²), which means that it's possible for observer B to be moving to the right faster than the incoming photons are moving to the right. Hence they exert a drag on B, i.e., a force in the negative x direction. When viewed in terms of the rest frame coordinates of B, the sources were to the right of B when they emitted those light pulses, even though the sources were to the left of B in terms of the rest frame coordinates of A. This illustrates how careful one must be to correctly account for the effective aberration of light pulses between moving objects, even if the objects are in simple uniform motion.

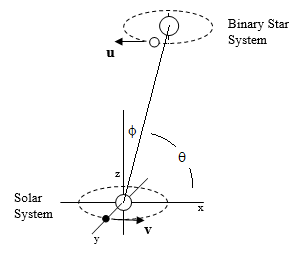
Of course, it isn’t necessary for the sources of light to be in uniform motion. For example, consider a binary star system in which one large central star is roughly stationary (relative to our Sun), and a smaller companion star is orbiting around the central star with a large orbital speed in a plane parallel to the plane of the Earth’s orbit, as illustrated in the figure below.

Let θ denote the angle of the light path (from both stars to Earth) in terms of the common rest frame of the Sun and the larger star, and let v and u denote the speeds (in opposite directions) of the Earth and the revolving star relative to that same frame. Also, let θʹ and θʺ denote the angles of the light path relative to the momentary rest frames of the Earth and the revolving star, respectively. Equation (1) gives

Now, suppose we wish to express the relationship between θʹ and θʺ directly in terms of the relative velocity between the Earth and the revolving star, without referring to the angle that the light path makes relative to the rest frame of the Sun. This is easily done, by simply solving the right hand equation above for cos(θ), and then substituting this into the left hand equation. The result is

The quantity V = (u+v)/(1+uv) is the velocity of the Earth relative to the momentary rest frame of the revolving star (in terms of which the angle of the light path is θʺ), so this can be written as

Thus equation (1) gives exactly the same result, whether the base reference frame is taken to be the Sun or the revolving star – or any other rest frame for that matter. People sometimes mistakenly try to apply equation (1) with some varying relative velocity V but using the original base angle θ, which is incorrect. The angle θ in equation (1) is defined as the angle of the light path in terms of whatever reference frame we choose as our base. Thus if we take a momentary rest frame of the revolving star as our base frame, and consider the speed V of the Earth relative to that frame, then the base angle on the right side of equation (1) must be θʺ, which is the angle of the light path in terms of that base frame. It so happens that the inertial coordinate system momentarily co-moving with the revolving star is continually changing, but regardless of which frame we choose, equation (1) gives the correct result, provided we use the corresponding base angle, i.e., the angle of the light path relative to our chosen base frame, which need not be the frame of the source. For example, we can choose as the base frame the rest frame of our Sun, or the rest frame of the Earth six months from now. The formula simply gives the relationship between the angles of a ray in terms of any two systems of inertial coordinates.

For a more detailed analysis of the aberration of light from binary stars in the perpendicular case, we must return to the basic metrical relations. In the situation described above, let us consider the special case θ = π/2, meaning the light ray from the stars is normal to the plane of the Earth’s orbit in terms of the Sun’s rest frame. The Earth is moving in its orbit with speed v relative to the frame of the Sun (and the distant central star), and the Earth is momentarily at rest at the origin of a system of inertial coordinates x,y,z,t, oriented so that the large central star of the distant binary pair at a distance L from the Earth has the coordinates x₁(t) = −vt, y₁(t) = 0, z₁(t) = L, t₁(t) = t. A pulse of light travels along null paths, so if a pulse is emitted from the star at time t = T and arrives at Earth at time t = 0, we have T² = (vT)² + L², and so T = −L/(1−v²)^1/2, from which it follows that x₁/z₁ at time T was v/(1−v²)^1/2. Thus, for the central star we have the aberration angle

The coordinates of the smaller star revolving at a radius R around the larger star in a plane perpendicular to the Earth are x₂(t) = −vt + Rcos(ψ), y₂(t) = Rsin(ψ), z₂(t) = L, and t₂(t) = t, where ψ is the angular position of the smaller star in its orbit. Again, since light travels along null paths, a pulse of light arriving on Earth at time t = 0 was emitted at time t = T satisfying the relation

Dividing through by L² and re-arranging terms, we have

Consequently, for L sufficiently great compared to R, the second two terms on the right side are negligible, so we have again T = −L/(1−v²)^1/2, and hence the tangents of the angles of incidence in the x and y directions are

The leading terms in these tangents represent just the inherent "static" angular separation between the two stars viewed from the Earth, and these angles are negligibly small for sufficiently large L. Thus the tangent of the aberration angle is (again) essentially just v/(1−v²)^1/2, and so, as before, we have sin(α) = v, which of course is the same as for the central star. As noted above, Bradley's original formula for aberration was tan(α) = v, whereas the corresponding relativistic equation is sin(α) = v. The actual aberration angles for stars seen from Earth are small enough that the sine and tangent are virtually indistinguishable.

As an aside, the experimental results of Michelson and Morley, based on beams of light pointed in various directions with respect to the Earth's motion around the Sun, can also be treated as aberration effects. Let the arm of Michelson's interferometer be of length L, and let it make an angle α with the direction of motion in the rest frame of the arm. We can establish inertial coordinates t,x,y in this frame, in terms of which the light pulse is emitted at t₁ = 0, x₁ = 0, y₁ = 0, reflected at t₂ = L, x₂ = Lcos(α), y₂ = Lsin(α), and arrives back at the origin at t₃ = 2L, x₃ = 0, y₃ = 0. The Lorentz transformation to a system x',y',t' moving with velocity v in the x direction is xʹ = (x−vt)γ, yʹ = y, tʹ = (t−vx)γ where γ² = 1/(1−v²), so the coordinates of the three events are x₁ʹ = 0, y₁ʹ = 0, t₁ʹ = 0, and x₂ʹ = L[cos(α)−v]γ, y₂ʹ = Lsin(α), t₂ʹ = L[1−vcos(α)]γ, and x₃ʹ = −2vLγ, y₃ʹ = 0, t₃ʹ = 2Lγ. Hence the total elapsed time in the primed coordinates is 2Lγ. Also, the total spatial distance traveled is the sum of the outward distance

and the return distance

so the total distance is 2Lγ, giving a light speed of 1 regardless of the values of v and α. Of course, the angle of the interferometer arm cannot be α with respect to the primed coordinates. The tangent of the angle equals the arm's y extent divided by its x extent, which gives tan(α) = Lsin(α)/[L(cos(α)] in the arm's rest coordinates. In the primed coordinates the yʹ extent of the arm is the same as the y extent, Lsin(α), but the xʹ extent is Lcos(α)γ, so the tangent of the arm's angle is tan(αʹ) = tan(α)γ. However, this should not be confused with the angle (in the primed coordinates) of the light pulse as it travels along the arm, because the arm is in motion with respect to the primed coordinates. The outward direction of motion of the light pulse is given by evaluating the primed coordinates of the emission and absorption events at x₁,y₁ and x₂,y₂ respectively. Likewise the inward direction of the light pulse is based on the interval from x₂,y₂ to x₃,y₃. These give the tangents of the outward and inward angles

Naturally these agree with the result of taking the ratio of equations (1) and (2).

Return to Table of Contents