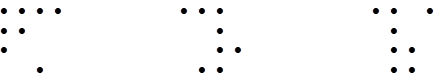4.1  Immovable Spacetime

My argument for the notion of space being really independent of body is founded on the possibility of the material universe being finite and move-able. 'Tis not enough for this learned writer [Leibniz] to reply that he thinks it would not have been wise and reasonable for God to have made the material universe finite and moveable… Neither is it sufficient barely to repeat his assertion that the motion of a finite material universe would be nothing, and (for want of other bodies to compare it with) would produce no discoverable change, unless he could disprove the instance which I gave of a very great change that would happen, viz., that the parts would be sensibly shocked by a sudden acceleration or stopping of the motion of the whole: to which instance, he has not attempted to give any answer.

                                          Samuel Clarke, 1716

Although the words "relativity" and "relational" share a common root, they refer to two quite different physical concepts. The principle of relativity asserts that for any material particle in any state of motion there exists a system of space and time coordinates in terms of which the particle is instantaneously at rest and inertia is homogeneous and isotropic. Thus the natural (inertial) decomposition of spacetime intervals into temporal and spatial components can be defined only relative to some particular frame of reference. On the other hand, the principle of relationism asserts that the absolute intervals between material objects fully characterize their extrinsic positional status, without reference to any underlying system of reference. From a purely relational point of view the concept of absolute inertia on which the principle of relativity is based has no meaning. Hence, relativity and relationism are fundamentally incompatible principles. Admittedly, during the years when Einstein was developing general relativity – and even for several years thereafter – he tended to conflate the two, since he hoped that the theory would vindicate Mach’s idea of a relational basis for inertia, but it soon became clear that general relativity is not a relational theory, at least not according to the traditional meaning of that term.

The traditional debate between proponents of relational and absolute motion (such as Leibniz and Clarke, respectively) is of questionable relevance if continuous fields are accepted as extended physical entities, permeating all of space, because this implies there are no unoccupied locations. In this context every point in the entire spacetime manifold is a vertex of actual relations between physical entities, obscuring the distinction between absolute and relational premises. Moreover, in the context of the general theory of relativity, spacetime itself constitutes a field, and this field is a dynamical elements in the theory, i.e., it is an extended physical entity which not only acts upon material objects but is also acted upon by them. This renders the distinction between absolute and relational concepts even more obscure. However, it remains (at least arguably) possible to regard fields as just abstract constructions with no ontological status, and to express all physical phenomena in terms of substantial entities possessing spatio-temporal attributes. In this context the absolute-relational question remains both relevant and unresolved.

Physicists have always recognized the appeal of a purely relational outlook, since our measurements seem to be always reducible to the determination of relations, and yet every such theory has foundered on the same problem, namely, the apparent absoluteness of acceleration. For example, when formulating the law of universal gravitation one of Newton’s greatest challenges was to account for the fact that the Moon is relationally stationary with respect to the Earth (i.e., the distance between Earth and Moon is roughly unchanging), whereas it ought to be accelerating toward the Earth due to the influence of gravity. What is holding the Earth and Moon apart? Or, to put the question differently, why is the Moon not accelerating directly toward the Earth in accord with the gravitational force that is presumably being applied to it? Newton's great insight was that the Moon is indeed accelerating directly toward the Earth, and with precisely the magnitude of acceleration predicted by the inverse-square law, but that the Moon is also moving perpendicularly to the Earth-Moon axis, with a velocity v = ωR, where R is the Earth-Moon distance and ω is the Moon's angular velocity, i.e., roughly 2π radians per moonth. If it were not accelerating toward the Earth, the Moon would just proceed tangentially away from the Earth, but the force of gravity is modifying its velocity by adding GM/R² ft/sec toward the Earth each second, which causes the Moon to turn continually in a roughly circular orbit around the Earth. The centripetal acceleration of an object revolving in a circle is v²/R = ω²R, and so (Newton reas oned) this must equal the gravitational acceleration. Thus we have ω² R³  =  GM, which of course is Kepler's third law.

But this explanation evidently depends on a strictly non-relational concept of motion. In fact, it might be said that the adoption of this non-relational view of motion was the crucial insight of Newtonian dynamics – and it applies no less in the special theory of relativity. For the purposes of dynamical analysis, motion must be referred to a particular class of rectilinear inertial coordinate systems, rather than simply to the relations between material bodies, or even to classical fields. Thus, according to Newton, we can not infer everything important about an object's state of motion simply from its distances to other objects (at least not to nearby objects). In this sense, both Newtonian and relativistic physics find it necessary to invoke a non-relational aspect of the spatio-temporal behavior of objects. The most natural way of representing this aspect seemed (to Newton) to be in terms of absolute space and time.

But this concept of absolute space presents us with an ontological puzzle, because we can empirically verify the physical equivalence of all inertial states of motion, which suggests that position and velocity have no absolute physical significance, and yet changes in velocity (i.e., accelerations) do appear to have absolute significance, independent of the relations between material bodies (at least locally). If the evident relativity of position and velocity lead us to discard the idea of absolute space, how are we to understand the apparent absoluteness of acceleration? Some have argued that in order for the change in something to be ontologically real, it is necessary for the thing itself to be real, but of course that's not the case. It's perfectly possible for "the thing itself" to be an artificial conception, whereas the "change" is the ontological entity. For example, the Newtonian concept of the physical world is a set of particles, between which there exist spatio-temporal relations. In this view, the primary ontological entities are the particles, and the relations are secondary, but it's equally possible to imagine that the separations are the "real" primary entities, and the imagined “particles” are merely a convenient bookkeeping device for organizing our knowledge about the separations. One hypothetical form for the law governing such separations is discussed in Section 4.2. However, the idea of taking separations as primary entities, dispensing with particles, leads to difficulties when we consider whether an unordered multi-set of n(n–1)/2 separations suffices to uniquely determine a configuration of n points in a space of fixed dimension. It isn't difficult to find examples of multi-sets of separations that allow for multiple distinct spatial arrangements of particles. For example, given the multi-set of ten separations

we can construct either of the two five-point configurations shown below

For another example, the following three distinct configurations of eight co-planar points each have the same multi-set of 28 point-to-point separations:

In fact, of the 12870 possible arrangements of eight points on a 4x4 grid, there are only 1120 distinct multi-sets of separations. Much of this reduction is due to rotations and reflections, but not all. Intrinsically distinct configurations of points with the same multi-set of distances are not uncommon. They are sometimes called isospectral sets, referring to the spectrum of point-to-point distances. Examples such as these may suggest that unordered separations cannot be the basis of our experience, although we can't rule out, a priori, the possibility that our interpretation of experience is non-unique, and that different states of consciousness might perceive a given physical configuration differently. Even if we reject the possibility of non-unique mapping to our conventional domain of objects, we could still imagine a separation-based ontology by stipulating the topology for those separations, assigning the connectivities corresponding to a unique configuration of particles. But by recognizing the need to specify this topology, our focus shifts back to a particle-based ontology.

As noted previously, according to both Galilean and Einsteinian (special) relativity, position and velocity are relative but acceleration is not. However, it can be argued that the absoluteness of acceleration is incongruous with Galilean spacetime, because if spacetime was Galilean there would be no reason for acceleration to be absolute. This was mentioned in the discussion of Section 1.8, where the cyclic symmetry of the velocity relations between three Galilean reference systems was noted. In a sense, the classical relationists such as Leibniz were correct in asserting that absolute space and time are inconsistent with Galilean relativity, citing the “principle of sufficient reason” in support of this claim. If time and space are separate and distinct (which no one had ever disputed) then there would be no observable distinction between accelerated and un-accelerated systems of reference, as revealed by the fact that the concept of a moveable rigid body of arbitrary size is perfectly consistent with the kinematics of Galilean relativity. Samuel Clarke had argued that if all the material in some finite universe was accelerated in tandem, maintaining all the intrinsic relations between the particles, this acceleration would still be physically real, even though no one could observe the acceleration (for lack of anything to compare with it). Leibniz replied

Motion does not indeed depend upon being observed, but it does depend upon being possible to be observed. There is no motion when there is no change that can be observed. And when there is no change that can be observed, there is no change at all. The contrary opinion is grounded upon the supposition of a real absolute space, which I have demonstratively confuted by the principle of the want of a sufficient reason of things.

It is quite right that, in the context of Galilean relativity, the acceleration of all the matter of the universe in tandem would be strictly unobservable, so Leibniz had a valid point. However, barring some Machian long-range influence which neither Clarke nor Leibniz seems to have imagined, the same argument implies that inertia should not exist at all. Thus Clarke was correct in pointing out that the very existence of inertia refutes Leibniz’s position. There is indeed an observable distinction between uniform and accelerated motion, i.e., inertia does exist. In summary, Leibniz was correct in (effectively) claiming that the existence of inertia is logically incompatible with the Galilean concept of space and time, whereas Clarke was correct in pointing out that inertia does actually exist. The only way out of this impasse would have been to discard the one premise that neither of them ever questioned, namely, the Galilean concept of space and time. It was another 200 years before a viable alternative to Galilean spacetime was recognized.

As described in Section 1, the spacetime structures of Galileo and Minkowski are formally identical if the characteristic constant c of the latter is infinite. In that case it follows that arbitrarily large rigid bodies are possible, so it is conceivable for all the material in an arbitrarily large region to accelerate in tandem, maintaining all the same intrinsic spatial relations. However, if c has some finite value, this is no longer the case. Section 2.9 described the kinematic limitation on the size of a spatial region in which objects can be accelerated in tandem. Hence the structure of Minkowski spacetime intrinsically distinguishes uniform motion as the only kind of motion that could be applied in tandem to all objects throughout space. In this context, Leibniz’s principle of sufficient reason can be used to argue that different states of uniform motion should not be regarded as physically different, but it cannot be applied to accelerated motion, because the very kinematics of Minkowski spacetime do not permit the tandem acceleration of objects over arbitrarily large regions. In this sense it is justifiable to say that the existence of inertia implies the Minkowski character of spacetime.

This goes some way towards resolving the epistemological problems that have often been raised against the principle of inertia. To the question “How are we to distinguish the inertial coordinate systems from all possible systems of reference?”, we can answer that the inertial coordinate systems are precisely those in terms of which two objects separated by an arbitrary distance can be accelerated in tandem. This doesn’t help to identify inertial coordinate systems in Galilean spacetime, but it fully identifies them in the context of Minkowski spacetime. So, it can be argued that (from an epistemological standpoint) Minkowski spacetime is the only satisfactory framework for the principle of inertia.

Still, there remain some legitimate open issues regarding any (so far) conceived relativistic spacetime. According to both classical and special relativity, the inertial coordinate systems are fully symmetrical, and each one is regarded as physically equivalent (in the absence of matter). In particular, we cannot single out one particular inertial system and claim that it is the "central" frame, because the equivalence class has no center, and all ontological qualities are uniformly distributed over the entire class. Unfortunately, from a purely formal standpoint, a purported uniform distribution over inertial frames is somewhat problematic, because the inertial systems of reference along a single line can only be linearly parameterized in terms of a variable that ranges from –∞ to +∞, such as q = log((1+v)/(1-v)), but if each value of q is to be regarded as equally probable (a priori), then we are required to imagine a perfectly uniform density distribution over the real numbers. Mathematically, no such distribution exists. To illustrate, imagine trying to select a number randomly from a uniform distribution of all the real numbers. This is the source of many well-known mathematical conundrums, such as the "High-Low Number" strategy game, whose answer depends on the fact that no perfectly uniform distribution exists over the real numbers (nor even over the integers). In trying to understand whether there was any arbitrary choice in the creation of the physical world, it’s interesting to note that the selection of our particular rest frame cannot have been perfectly arbitrary from a set of pre-existing alternatives. It might be argued that the impossibility of a choice between indistinguishable inertial reference frames implies that only an absolutist framework is intelligible. However, the identity of indiscernibles led Leibniz and Mach to argue just the opposite, i.e., that the only intelligible way to imagine the existence of objects, all in roughly the same frame of reference within a perfectly symmetrical class of possible reference systems, is to imagine that the objects themselves are in some way responsible for the class, which brings us back to pure relationism.

Alas, as we’ve seen, pure relationism has its own problematic implications. For one, there has traditionally been a close association between relationism and the concept of absolute simultaneity. This is because the “relations” were regarded as purely spatial, and it was necessary to posit a unique instant of time in which to evaluate those spatial relations. To implement a spatial relationist theory in the framework of Minkowski spacetime would evidently require that whatever laws apply to the spatial relations for one particular decomposition of spacetime must also apply to all other decompositions. (A simple example of this is discussed in Section 4.2.) Alternatively, we might say that only invariant quantities should be subject to the relational laws, but this amounts to the same thing as requiring that the laws apply to all decompositions.

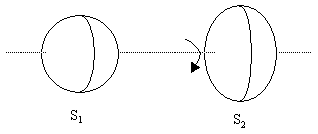
One common feature of all purely relational models based on Galilean space and time is their evident non-locality, because (as noted above) there is no way, if we limit ourselves to local observations, to identify the inertial motions of material objects purely from the kinematical relations between them. We're forced to attribute the distinction between inertial and non-inertial motion to some non-material (or non-local) interaction. This is nicely illustrated by Einstein's thought experiment (based on Newton's famous "spinning pail") involving two nominally identical fluid globes S₁ and S₂ floating in an empty region of space. One of these globes is set rotating (about their common axis) while the other remains stationary. The rotating globe assumes an oblate shape due to its rotation.

If globes are mutually stationary and not rotating, they are both spherical and symmetrical, and we cannot distinguish between them, but if one of the globes is spinning about their common axis, the principle of inertia leads us to expect that the spinning globe will bulge at the "equator" and shrink along its axis of rotation due to the centripetal forces. The "paradox" (for the relationist) is that each globe is spinning with respect to the other, so they must still be regarded as perfectly symmetrical, and yet their shapes are no longer congruent. To what can we attribute the asymmetry?

Oddly enough, it doesn’t seem to have occurred to many relationists to challenge such examples based on the law of action and re-action, or equivalently, the conservation of angular momentum. (By the same token, when responding to Clarke’s scenario of an accelerating universe having all the same intrinsic relations as a stationary one, Leibniz failed to point out that such a thing violates Newton’s law of action and reaction.) The described situation is clearly incomplete, because some other material must have acted upon the right hand globe to set it spinning, and an equal and opposite angular momentum must have been imparted to that other material, so the apparently inexplicable asymmetry between the two globes shown is simply due to the neglect of the other interacting material. In this sense, the conservation of momentum ensures that a relational account of acceleration can always be given.

Although the classical relationists didn’t appeal to action and re-action directly, they did point out that the deformed globe is rotating relative to all the distant stars, whereas the spherical globe is not. A little experimentation shows that a globe's deformation is strictly a function of its speed of rotation relative to the distant stars, and even without recognizing the link provided by the action-reaction principle, they felt entitled to suggest that this could not be a mere coincidence. Newton's explanation for this coincidence (rather than invoking his own third law) was to argue philosophically that the local globes and the distant stars all reside in the same absolute space, and it is this space that defines absolute (inertial) motion, and likewise the special relativistic theory invokes an absolutely preferred class of reference frames. Even in the general theory of relativity, when viewed from a specific cosmological perspective, there is always a preferred frame of reference, owing to the global boundary conditions that must be imposed in order to single out a solution. This came as a shock to Einstein himself at first, since (as mentioned above) he originally imagined that the field equations of general relativity represented true relationism, but his conversion began when he received Schwarzschild's exact solution for spherical symmetry, which of course exhibits a preferred coordinate system such that the metric coefficients are independent of time, i.e., the usual Schwarzschild coordinates, which are essentially unique for that particular solution.

Likewise for any given solution there is some globally unique system of reference singled out by symmetry or boundary conditions (even for asymptotically flat universes, as Einstein himself showed). For example, in the Friedman "big bang" cosmologies there is a preferred global system of coordinates corresponding to the worldlines with respect to which the cosmic background radiation is isotropic. Of course, this is not a fresh insight. The non-relational global aspects of general relativistic cosmologies have been extensively studied, beginning with Einstein's 1917 paper on the subject, and continuing with Gödel's rotating empty universes, and so on. Such examples make it clear that general relativity is not a relational theory of motion, because it does not correlate all physical effects with the relations between material bodies, but rather with the relations between objects (including fields) and the absolute background metric, which is affected by, but is not determined by, the distribution of objects (except arguably in closed cosmological models). Thus relativity, no less than Newtonian mechanics, relies on spacetime as an absolute entity in itself, exerting influence on fields and material bodies. The extra information contained in the metric of spacetime is typically introduced by means of boundary conditions or "initial values" on a spacelike foliation, sufficient to fix a solution of the field equations.

In this way relativity very quickly disappointed its early logical-positivist supporters when it became clear that it was not, and never had been, a relational theory of motion, in the sense of Leibniz, Berkeley, or Mach. Initially even Einstein was disturbed by the Schwarzschild and de Sitter solutions (see Section 7.6), which represent complete metrical manifolds with only one material object or none at all (respectively). These examples showed that spacetime in the theory of relativity cannot simply be regarded as the totality of the extrinsic relations between material objects (and non-gravitational fields), but is a primary physical entity of the theory, with its own absolute properties, most notably the metric with its related invariants, at each point. Indeed this was Einstein's eventual answer to Mach's critique of pre-relativity physics. Mach had complained that it was unacceptable for our theories to contain elements (such as spacetime) that act on (i.e., have an effect on) other things, but that are not acted upon by other things. Mach, and the other relationists before him, naturally expected this to be resolved by eliminating spacetime, i.e., by denying that an entity called "spacetime" acts in any physical way. To Mach's surprise (and unhappiness), the theory of relativity actually did just the opposite - it satisfied Mach's criticism by instead making spacetime a full-fledged dynamical element of theory, acted upon by other objects. By so doing, Einstein believed he had responded to Mach's critique, but of course Mach hated it, and said so. Early in his career, Einstein was sympathetic to the idea of relationism, and entertained hopes of banishing absolute space from physics but, like Newton before him, he was forced to abandon this hope in order to produce a theory that satisfactorily represents our observations.

The absolute significance of spacetime in the theory of relativity was already obvious from trivial considerations of the special theory. The twins paradox is a good illustration of why relativity cannot be a relational (and local) theory, because the relation between the twins is perfectly symmetrical, i.e., the spatial distance between them starts at zero, increases to some maximum value, and then decreases back to zero. The distinction between the twins cannot be expressed in terms of their mutual relations to each other, but only in terms of how each of their individual worldlines are embedded in the absolute metrical manifold of spacetime. This becomes even more obvious in the context of general relativity, because we can then have multiple distinct geodesic paths between two given events, with different lapses of proper time, so we cannot even appeal to any difference in "felt" accelerations or local physics of any kind along the two world-paths to account for the asymmetry. Hopes of accounting for this asymmetry by reference to the distant stars, ala Mach, were certainly not fulfilled by general relativity, according to which the metric of spacetime is conditioned by the presence of matter, but only to a very slight degree in most circumstances. From an overall cosmological standpoint we are unable to attribute the basic inertial field to the configuration of mass and energy, and we have no choice but to simply assume a plausible absolute inertial background field, just as in Newtonian physics, in order to actually make predictions and solve problems. This is necessarily a separate and largely independent stipulation from our assumed distribution of matter and energy. Of course, since the metrical field itself plays the role of a dynamical entity in general relativity, one could argue that the stipulation of a background spacetime has, after all, a relationist meaning. The legitimacy of this argument rests on a very subtle feature of general relativity, because although a curved metrical field can be said to possess energy, the equivalence principle implies that it is not possible to localize the energy of this field. At any given event we can consider a free-falling coordinate system, and conclude that there is no gravitational energy at that event. Only in the context of an asymptotically flat surrounding spacetime can we determine the gravitational energy contained within some defined region. This is why the historical debate between relational and absolute theories becomes ambiguous in the context of general relativity. On the other hand, special relativity is arguably a strongly absolute theory, even more so than was the relativity of Galileo and Newton.

To understand why Galilean relativity is actually more relational than special relativity, note that the unified spacetime manifold with the lightcone structure of Minkowski spacetime is more rigid than a pure Cartesian product of a three-dimensional spatial manifold and an independent one-dimensional temporal manifold. In Galilean spacetime at a spatial point P₀ and time t₀ there is no restriction at all on the set of spatial points at t₀ + dt that may "spatially coincide with P₀" with respect to some valid inertial frame of reference. In other words, an inertial worldline through P₀ at time t₀ can pass through any point in the entire universe at time t₀ + dt for any positive dt. In contrast, the lightcone structure of Minkowski spacetime restricts the future of the point P₀ to points inside the future null cone, i.e., P₀ ± cdt, and as dt goes to zero, this range goes to zero, imposing a well-defined unique connection from each "infinitesimal" instant to the next, which of course is what the unification of space and time into a single continuum accomplishes.

We referred above to Newtonian spacetime without distinguishing it from what has come to be called Galilean spacetime. This is because Newton's laws are manifestly invariant under Galilean transformations, and in view of this it would seem that Newton should be counted as an advocate of relativistic spacetime. However, in several famous passages of the first Scholium of the Principia Newton seems to reject the very relativity on which his physics is founded, and to insist on distinctly metaphysical conceptions of absolute space and time. He wrote

I do not define the words time, space, place, and motion, since they are well known to all. However, I note that people commonly conceive of these quantities solely in terms of the relations between the objects of sense perception, and this is the source of certain preconceptions, for the dispelling of which it is useful to distinguish between absolute and relative, true and apparent, mathematical and common.

It isn't trivial to unpack the intended significance of these statements, especially because Newton has supplied three alternate names for each of the two types of quantities that he wishes us to distinguish. On one hand we have absolute, true, mathematical quantities, and on the other we have relative, apparent, common quantities. The latter are understood to be founded on our sense perceptions, so the former presumably are not, which would make them metaphysical. However, Newton also says that this distinction is useful for dispelling certain prejudices, which suggests that his words are intended to serve a utilitarian and/or pedagogical purpose rather than to establish an ontology. He continues

Absolute, true, and mathematical time, in and of itself and of its own nature flows uniformly (equably), without reference to anything external. By another name it is called duration. Relative, apparent, and common time is any sensible external measure of duration by means of motion. Such measures (for example, an hour, a day, a month, a year) are commonly used instead of true time.

Absolute space, in its own nature, without relation to anything external, remains always similar and immovable. Relative space is some movable measure of absolute space, which our senses determine by the positions of bodies... Absolute and relative space are of the same type (species) and magnitude, but are not always numerically the same...

Place is a part of space which a body takes up, and is according to the space either absolute or relative.

Absolute motion is the translation of a body from one absolute place to another, and relative motion is the translation from one relative place to another.

Newton's insistence on the necessity of referring all true motions to "immovable space" has often puzzled historians of science, because it's easy to see that his actual formulation of the laws of physics is invariant under Galilean transformations, and that the concept of absolute motion plays no role. Each and every mention of a "state of rest" in Newton’s definitions and laws is accompanied by the phrase "or uniform motion in a right line", so the system built on these axioms explicitly does not distinguish between these two concepts. What, then, did Newton mean when he wrote that true motions must be referred to immovable space?

The introductory Scholium ends with a promise to explain how the true motions of objects are to be determined, declaring that this was the purpose for which the Principia was composed, so it's all the more surprising to find that the subject is never even mentioned in Books I or II. Only in the concluding Book III, "The System of the World", does Newton return to this subject, and we finally learn what he means by "immovable space". Although he famously asserted that "I frame no hypotheses", we find immediately following Proposition X in Book III (in the third edition) the singular hypothesis

HYPOTHESIS I:  That the centre of the system of the world is immovable.

In support of this remarkable assertion, Newton simply says "This is acknowledged by all, although some contend that the earth, others that the sun, is fixed in that centre." In the subsequent proposition XI we finally discover Newton's immovable space. He writes

PROPOSITION XI:  That the common centre of gravity of the earth, the sun, and all the planets, is immovable. For that centre either is at rest or moves uniformly forwards in a right line; but if that centre moved, the center of [the system of] the world would move also, against the Hypothesis.

Thus Newton asserts that the center of mass of the solar system (which he calls the “system of the world”) is absolutely at rest, although he acknowledges that according to the laws he has enunciated it could also be moving uniformly in a straight line. This makes it clear that Newton's purpose all along has been not to deny Galilean relativity or the fundamental principle of inertia (i.e., the equivalence of rest and uniform motion in a straight line) on which his physics is based, but simply to show that a suitable system of reference for determining true inertial motions need not be centered on some material body. This was foreshadowed in the first Scholium when he wrote "it may be that there is no body really at rest, to which the places and motions of others may be referred".

Furthermore, he notes that many people believed the immovable center of the system of the world was at the center of the Earth, whereas others followed Copernicus in thinking the Sun was the immovable center. Newton evidently (and rightly) regarded it as one of the most significant conclusions of his deliberations that the true inertial center of the system of the world was in neither of those objects, but is instead the center of mass of the entire solar system. We recall that Galileo found himself in trouble for claiming that the Earth moves, whereas both he and Copernicus believed that the Sun was absolutely stationary. Newton showed that the Sun itself moves, as he continues

PROPOSITION XII:  That the sun is agitated by a continual motion, but never recedes far from the common centre of gravity of all the planets. For since the quantity of matter in the sun is to the quantity of matter in Jupiter as 1067 to 1, and the distance to Jupiter from the sun is to the semidiameter of the sun is in a slightly greater proportion, the common center of gravity of Jupiter and the sun will fall upon a point a little without the surface of the sun.

This was certainly a magnificent discovery, worthy of being called the purpose for which the Principia was composed, and it is clearly what Newton had in mind when he wrote the introductory Scholium promising to reveal how immovable space (i.e., the center of the system of the world – meaning the solar system) is to be found. In this context we can see that Newton was not claiming the ability to determine absolute rest, but rather the ability to infer from phenomena a state of absolute inertial motion, which he sensibly enough identified with the center of mass of the solar system. He very conspicuously labels as a Hypothesis (one of only three in the final edition of the Principia) the conventional statement, "acknowledged by all", that the center of the system of the world is immovable. By these statements he was trying to justify calling the solar system's inertial center the center of the system of the world, while specifically acknowledging that the immovability of this point is conventional, since it could just as well be regarded as moving "uniformly forwards in a right line".

The modern confusion over Newton's first Scholium arises from trying to impose an ontological interpretation on a 17th century attempt to isolate the concept of pure inertia, and incidentally to locate the center of “the system of the world" – by which he explicitly meant the solar system. It was essential for Newton to make sure his readers understood that "uniform motion" and "right lines" cannot generally be judged with reference to neighboring bodies (such as the Earth's spinning surface), because those bodies themselves are typically in non-uniform motion. Hence he needed to convey the fact that the seat of inertia is not the Earth's center, nor the Sun’s, nor any other material body, but is instead absolute space and time in precisely the same sense that spacetime is absolute in special relativity. This is distinct from asserting an absolute state of rest, which Newton explicitly recognized as a matter of convention.

Indeed, we now know the solar system itself revolves around the center of the galaxy, which itself moves with respect to other galaxies, so under Hypothesis I we must conclude that Proposition XI is strictly false. Nevertheless, the deviations from true inertial motion represented by those stellar and galactic motions are so slight that Newton's immovable center of “the system of the world" is still suitable as the basis of true inertial motion for nearly all purposes. In a more profound sense, the concept of "immovable space" been carried over into general relativity because, as Einstein said, spacetime is endowed with physical qualities that enable it to establish the local inertial frames, but "the idea of motion may not be applied to it".

Return to Table of Contents