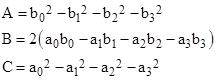4.2  Inertial and Gravitational Separations

And I am dumb to tell a weather’s wind

How time has ticked a heaven round the stars.

                            Dylan Thomas, 1934

Special relativity, no less than Galilean relativity, presupposes a three-dimensional space, within which individual physical entities exist and move over time. Each localized entity (such as a particle or a point of a field) has, at any given time, a position in space that can be characterized by three real numbers, representing the spatial coordinates of the entity, and all the spatial relations between entities can be inferred from these coordinates. Hence, given N point-like entities, the N(N−1)/2 spatial distances between pairs of entities (at a given time) can be encoded as the 3N coordinates of those particles. From a purely relational point of view, without presupposing any embedding in a manifold with a fixed number of dimensions, we have no reason to expect such a reduction in the degrees of freedom. Each of the N(N-1)/2 pair-wise separations could be regarded as an independent quantity. The apparent fact that these separations are not independent, but can be encoded in the form of N sets of three numbers, which vary continuously with time, provides the justification for the idea of particles moving in a coherent three-dimensional space, and is one of the strongest arguments against the possibility of a purely relational basis for physical theories – unless we include space (or spacetime) itself as a dynamical entity.

If we insist on a purely relational theory, with no background space, one could argue that the separations between entities ought to be regarded as the primary ontological entities, with the particles serving merely abstract concepts to organize our knowledge of those separations. The relationist view doesn’t even presuppose a definite dimensionality of space, since each “separation” could be considered to represent an independent degree of freedom, absent any additional restricting principles. Of course, this freedom doesn’t seem to exist in the real world, since (for example) we cannot arrange five particles all mutually equidistant from each other. Nevertheless, it’s an interesting exercise to focus on the spatial separations that exist between material particles, rather than on the space and time coordinates of individual particles, to see if the behavior of these separations can be characterized in a simple way.

From the conventional point of view, the simplest motion is that of a free particle moving inertially, i.e., in a straight line at uniform speed, which can be described by saying that the space coordinates are linear functions of the time coordinate (assuming a system of inertial coordinates). From a relational standpoint, we consider the spatial separation between two such particles. The three orthogonal components Δx, Δy, and Δz of the separation are linear functions of time, i.e.,

where the coefficients a_i and b_i are constants. Therefore the magnitude of any such "co-inertial” separation is of the form

where

Letting the subscript n denote nth derivative with respect to time, the first two derivatives of s(t) are

The right hand equation shows that s₂ s₀³ = k, and we can differentiate this again and divide the result by s₀² to show that the separation s(t) between any two particles in relatively unaccelerated (i.e., co-inertial) motion in Galilean spacetime must satisfy the equation

Next, consider a particle of mass m attached to a rod in such a way that it can slide freely along the rod. If we rotate the rod about some fixed point, the particle will tend to slide outward along the rod away from the center of rotation in accord with the basic equation of motion

where s is the distance from the center of rotation to the sliding particle, and ω is the angular velocity of the rod. Differentiating and multiplying through by s₀ gives

Then since s₂ = ω²s₀, we see that s(t) satisfies the equation

which is formally similar to (1).

For a final example, consider the separation between two massive particles in gravitational free-fall due to their mutual gravitational attraction. Assume the two particles are identical, each of mass m, lying along a line that is not rotating. According to Newtonian theory the equation for this separation is

where G is a universal constant. Note that each particle's "absolute" acceleration is half of the second derivative of their mutual separation with respect to time. Re-arranging terms, we have s₂ s₀² = −2Gm. Differentiating this again and dividing through by s₀, we can characterize radial gravitational free-fall by the purely kinematic equation

So, we find once again that a common (albeit idealized) class of physical separations satisfies the same form of differential equation, even though in this case the separation is governed by gravitation rather than just kinematics and inertia. All these separations are characterized by an equation of the form

for some constant N. (Among the other solutions of this equation, with N = −1, are the elementary transcendental functions e^t, sin(t), and cos(t). Solving for N, to isolate the arbitrary constant, we have

Differentiating both sides, we get the basic equation

If none of s₀, s₁, s₂, and s₃ is zero, we can divide each term by all of these to give the aesthetically appealing form

This could be seen as a (admittedly very simplistic) “unification” of a variety of physically meaningful spatial separations under a single equation. However, this obviously doesn’t encompass more than a tiny fraction of the variety of spatial separations in the physical world. In fact, it’s clear that the objects of our experience, viewed in isolation, cannot possibly be fully characterized by just their mutual separations. For example, the separation between two massive particles, as discussed above, beginning from a given stationary value, will shrink to zero due to gravitational collapse, but only if the system of particles has no angular momentum. If the particles are revolving about their common center of mass at a suitable speed, the separation between them can remain constant. Thus we have distinct outcomes for a single intrinsic configuration. This is similar to Newton’s thought experiment with the rotating pail of water, and it is another reason that Newton founded his physics on the idea of absolute space, rather than on a purely relational basis. Of course, as Mach observed, the evident physical effects of “absolute rotation” don’t necessarily refute relationism as a viable basis for coordinating events. It may be that we must take more relations into account. For example, even though the two revolving particles are intrinsically identical to two stationary particles, the configurations are distinct when the relations of the particles to surrounding objects are considered. From this point of view, we wouldn’t expect to be able to treat individual separations, or even a limited cluster of related separations, in isolation. It would presumably be necessary to account for all separations in the universe in order to correctly analyze any part of the universe. This might seem to make relationism hopeless, but most attempts to construct such a theory have invoked simplifying assumptions about the aggregate effects of very distant separations.

Newton’s achievement was finding a way to analyze isolated parts of the world without having to explicitly refer to the rest of the universe. All the effects of the distant universe can be encoded in the simple concept of inertia in absolute space and time. To illustrate this approach, and to show how it relates to the separation equation discussed above, consider the general Newtonian equation of motion of a particle in a stationary spherical gravitational field:

In these equations, r is the magnitude of the distance of the particle from the center of the field and ω is the absolute angular velocity of the particle. A single coherent system of coordinates, with a single definition of absolute rotation, suffices for the analysis of all physical systems. We have no right to expect this to be true, but our experience has taught us that it is true. Now, if we solve the left hand equation for ω and differentiate to give dω/dt, we can substitute these expressions into the right hand equation and re-arrange the terms to give

which applies (in the Newtonian limit) to arbitrary free paths of test particles in a gravitational field. Obviously if m = 0 this reduces to equation (1), representing free inertial separations, whereas for purely radial motion we have d²r/dt² = −m/r², so this reduces to equation (3), representing radial gravitational separation.

Incidentally, even though the above has been based on the Galilean spatial separations between objects as a function of Galilean time, the same conditions can be shown to apply to the absolute spacetime intervals between inertial particles as a function of their proper times. Relative to any point on the worldline of one particle, the four components Δt, Δx, Δy, and Δz of the absolute interval to any other inertially moving particle are all linear functions of the proper time τ along the latter particle's worldline. Therefore, the components can be written in the form

where the coefficients a_i and b_i are constants. It follows that the absolute magnitude of any "co-inertial separation" is of the form

where

Thus we have the same formal dependence as before, except now the parameter s represents the absolute spacetime separation. This shows that the absolute separation between any fixed point on one inertial worldline and a point advancing along any other inertial worldline satisfies equation (1), where subscripts denote derivatives with respect to proper time of the advancing point. Naturally the reciprocal relation also holds, as well as the absolute separation between two points, each advancing along arbitrary inertial worldlines, correlated according to their respective proper times.

Return to Table of Contents