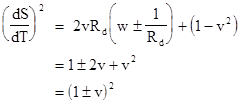4.8  The Breakdown of Simultaneity

I have yielded: Instruct my daughter how she shall

persever, that time and place with this deceit so

lawful may prove coherent.

               William Shakespeare, 1603

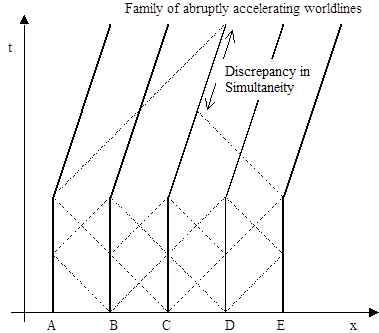
We've seen how the operational time convention enables us to define surfaces of simultaneity with respect to any given inertial frame. However, if we try to apply this procedure to a set of accelerating bodies the concept breaks down. The problem is illustrated in the spacetime diagram shown below.

This drawing shows a family of worldlines, each having the identical history of velocity as a function of time relative to the inertial coordinates. By sending light beams back and forth to its neighboring worldlines, an observer following path B can determine that he is equidistant from A and C. Likewise an observer on C is equidistant between B and D, and an observer on D is equidistant from C and E. However, due to the change in velocity of these worldlines, an observer on C can not conclude that he is equidistant from A and E. This breakdown of the well-defined locus of simultaneity is unavoidable in accelerating systems, because the operational procedure defining simultaneity involves a non-zero lapse of time for spatially separate objects, so the simultaneity relations change during the performance of the procedure. Of course, the greater the distance between objects, the greater the change in velocity (and simultaneity relations) during the performance of a synchronization procedure.

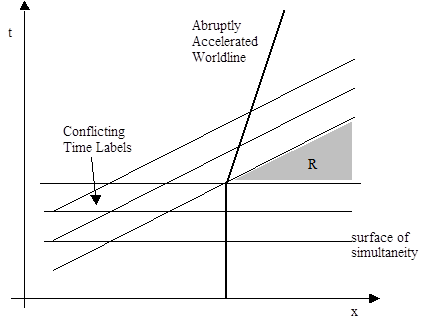
Another illustration of this problem is shown below, where the instantaneous loci of simultaneity of an abruptly accelerated worldline are seen to intersect each other (on the left), so that a given distant event is assigned multiple times of occurrence. Furthermore, events in the region "R" on the right do not properly correspond to any time according to the accelerating worldline's instantaneous inertial time, because at the instant of acceleration his locus of simultaneity jumps abruptly.

Obviously any amount of relative "skew" between the planes of simultaneity for a given worldline will result in interference at some distance, producing non-unique time coordinates. However, if the velocity of our worldline varies continuously (instead of abruptly), then for some limited region the planes of simultaneity will be advancing forward in time faster than they are "tilting" backwards, so over this limited region we can, if we choose, make use of these planes of simultaneity for the time labels of events. This situation is illustrated below.

x

We can easily determine the approximate limit for unique time labels with this kind of coordinate system by noting that if the velocity changes by amount dv/c during a time interval dt, then the relative slope of the new plane of simultaneity is c/dv, so it intersects with the original plane of simultaneity at a distance dx = (cdt)(c/dv) = c²/(dv/dt). Since  a = dv/dt is the acceleration, we can estimate that this accelerating system of coordinates is coherent out to distances on the order of c²/a.

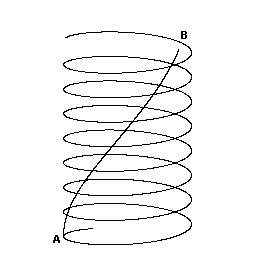
As an example of the use of accelerating coordinate systems and the breakdown of inertial simultaneity, consider a circular Sagnac device as described in Section 2.7. As we've seen, each point on the rim of the rotating disk can be associated with an instantaneously co-moving inertial coordinate system, each with its own surfaces of simultaneity. However, since each point of the disk is accelerating with respect to each other point, there is no coherent simultaneity (in the inertial sense) shared by any two points. If we analytically continue the local simultaneity from one point to the next around the perimeter, the result is an open helical surface as indicated below:

The worldline of a particular point on the rim is shown by the helical curve AB, and the shallower helix represents the analytically continued surface of inertial simultaneity. (It's interesting to compare this construction with Riemann surfaces in complex function analysis.)

Of course, we can dispense with the use of local inertial simultaneity to define our constant-t coordinate surfaces, and simply define an arbitrary system of space and time coordinates in terms of which a rotating disk is stationary (for example), but we then must be careful to correctly account for non-inertial aspects of these accelerating coordinates, particularly with regard to the meanings of spatial lengths. The usual intuitive definition of the spatial length of an object (such as the perimeter of the rim) is the absolute length of a locus of inertially simultaneous points of that object, so it depends on the establishment of a slice of "inertial simultaneity" over the entire rim. If we use inertial coordinates this is easy, but if we use non-inertial coordinates (such as those in which the rotating disk is stationary), then no surface of inertial simultaneity coincides with our surfaces of constant time parameter. In fact, this is essentially the definition of non-inertial coordinates. So, we will obviously be unable to define a coherent locus of inertial simultaneity over the whole disk as a surface of constant time parameter when working with non-inertial coordinates.

One consequence of this is the fact that the spatial length of a path becomes dependent on the speed of the path. We are accustomed to this for temporal lengths, i.e., the length of time around the rim might be 30 seconds or 2 hours or 1 nanosecond, etc., depending on how fast we are going relative to the disk, how fast the rim is spinning, in which direction it is spinning, and so on. Likewise the spatial length of a path around the rim (in terms of some particular coordinates) depends on the speed of the path. This shouldn't be surprising, because the decomposition of spacetime into separate spatial and temporal components is not unique, i.e., there are multiple equally self-consistent decompositions.

Since this is often a source of confusion, it's worthwhile to describe how this works in detail. Let's first establish inertial cylindrical coordinates in 2+1 spacetime, using polar coordinates (r,θ) for the space (where θ is the angular coordinate), and t for time. The metric in terms of these inertial coordinates is

and for any fixed time t the purely spatial metric is

So, to find the "length" of any spacelike curve, such as the perimeter of a spinning disk of radius r_d centered at the origin, we simply integrate ds over this curve at the fixed value of t. For a circular disk, r = r_d is constant, so dr = 0, and the spatial metric is simply ds = r_d dθ, which we integrate from θ = 0 to 2π to give the length 2π r_d.

Now let's look at this situation in terms of a system of coordinates in which the spinning disk is stationary, i.e., such that a fixed point anywhere on the disk maintains constant spatial coordinates for all values of the temporal coordinate. Taking the most naive and simplistic approach, let's define the new coordinates T,R,α by the relations

where ω is a constant, denoting the angular speed of these coordinates with respect to the inertial t,r,θ coordinates. We also have the differentials

Substituting these expressions into the metric equation gives

According to these coordinates, a spatial length S must be given by integrating the absolute spacelike differential using the metric along some constant-T surface, i.e., with dT = 0, where the metric is

Again for the perimeter of the disk we get 2π R_d = 2π r_d. Notice that our constant-T surfaces are also constant-t surfaces, so this perimeter length agrees with our previous result, and of course it doesn't matter which direction we integrate around the perimeter.

Incidentally, letting  v = R_d ω  denote the velocity of the rim with respect to the original inertial coordinates, the full spacetime metric for the rim (R = R_d) in terms of the rotating coordinates is

For a point fixed on the rim we have dα = 0, and so

which confirms that the lapse of proper time for a point fixed on the rim of the rotating disk is  times the lapse of T (and therefore of t).

Now let's send light beams around the perimeter in opposite directions. For lightlike paths we have dτ = 0, so the path of light must satisfy

The purely spatial component is dS = R_d dα, so we can make this substitution and divide both sides by (dT)² to give

The quantity dS/dT is the "speed of light" in terms of these rotating non-inertial coordinates. Also, from the definitions we have

where dθ/dt is the angular velocity of the light at radius R_d with respect to the inertial coordinates, so it equals ±1/R_d (noting that c = 1 in our units), with the sign depending on whether the light is clockwise or counter-clockwise. Substituting into the previous expression gives

Letting C = dS/dT denote the speed of light with respect to these rotating non-inertial coordinates, we therefore have C = 1 ± v, where again the sign depends on the direction of the light relative to the direction of rotation of the disk.

Does this analysis lead to some kind of paradox? It indicates that the non-inertial "speed of light" with respect to these rotating coordinates is not equal to 1, and in fact the ratio of the speeds in the two directions is (1+v)/(1–v), but of course this doesn't conflict with special relativity, because these are not inertial coordinates (due to their rotation). However, suppose we increase R_d and decrease w in proportion so that the rim speed v remains constant. The above formulas still apply for arbitrarily large R_d and small angular speed w, and yet the speed ratio remains the same, (1+v)/(1–v). Does this conflict with special relativity in the limit as the radius goes to infinity and the angular speed of the rim goes to zero? Clearly not, since we saw in Section 2.7 that if t₁ and t₂ denote the travel times for light pulses circling the disk in opposite directions, as measured by a clock at a fixed point on the rim, so that t₂/t₁ = (1+v)/(1–v), then we have t₂/t₁ – 1  =  ϕ/π, where ϕ is the angular travel of the disk during the transit of light. In other words, the observed ratio of travel times around the rim always differs from 1 by an amount proportional to the angular travel of the disk during the transit of light. Thus the net acceleration (change of velocity) of the rim observer during the measurement remains in constant proportion to the measured anisotropy of the transit times.

However, even without waiting for the light rays to circle the disk and report their anisotropy, don't the above formulas imply that the speeds of light in the two directions are in the ratio of (1+v)/(1–v) instantaneously with respect to our rotating coordinates, and don't the rotating coordinates approach being inertial coordinates as R_d increases while holding v constant? Yes and no. Both sets of coordinates use the same time t = T, but they use different space coordinates, s and S. For the perimeter of the disk we have

where W = dθ/dt. Thus the ratio dS/ds of spatial distances along a given "path" depends on the angular speed W of the path. Recall that for a signal travelling at c = 1 (with respect to the inertial coordinates) around the perimeter we have W = ±1/r_d, and so

This is consistent with the velocity ratio

This shows that the "spatial distances" around the perimeter are different in the two directions. But we saw earlier that "the spatial distance" was independent of the direction in which we integrated around the perimeter, even in the rotating coordinate system, so does this indicate an inconsistency? No, because, as noted above, the ratio dS/ds along a given path depends on the speed of the path. We have dS/ds = 1 + w/W, and for the perimeter of the disk with rim speed v and for a path with speed ±V, this gives

If the path is lightlike, we have V = 1 and so dS/ds = 1 ± v, whereas when we considered the purely spatial distance around the perimeter we took the "instantaneous" distance, i.e., we took a spacelike path with V = ∞, in which case dS/ds = 1 in both directions. This explains quantitatively what we mean when we say that we are measuring different things, depending on what spacetime path is having it's "spatial length" evaluated. Just as the temporal length of a path around the rim depends on the speed of the path, so too does the spatial length.

By the way, notice that if we integrate the spatial component of a path whose velocity V (relative to the original inertial coordinates) is the same as the rim speed itself, so that v = V, then obviously we will never move with respect to the disk in one direction, so dS = 0 and therefore dS/ds = 0, whereas in the other direction we have dS/ds = 2. Similarly if V = 0 we will never move relative to the original coordinates, i.e., ds = 0 and therefore dS/ds is infinite along such a path.

Return to Table of Contents