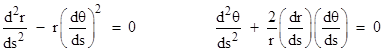5.6  The Equivalence Principle

The important thing is this: to be able at any moment to sacrifice what we are for what we could become.

                                                   Charles du Bos

At the end of a review article on special relativity in 1907, in which he surveyed the stunning range and power of the relativity principle, Einstein included a section discussing the possibility of extending the idea still further.

So far we have applied the principle of relativity, i.e., the assumption that physical laws are independent of the state of motion of the reference system, only to unaccelerated reference systems. Is it conceivable that the principle of relativity also applies to systems that are accelerated relative to each other?

This might have been regarded as merely a kinematic question, with no new physical content, since we can obviously re-formulate physical laws to make them applicable in terms of alternative systems of coordinates. However, as Einstein later recalled, the thought occurred to him while writing this paper that a person in gravitational free-fall doesn’t feel their own weight. It’s as if the gravitational field does not exist. This is remarkably similar to Galileo’s realization (three centuries earlier) that, for a person in uniform motion, it is as if the motion does not exist. Interestingly, Galileo is also closely associated with the fact that a (homogeneous) gravitational field can be “transformed away” by a state of motion, because he was among the first to explicitly recognize the equality of inertial and gravitational mass. As a consequence of this equality, the free-fall path of a small test particle in a gravitational field is independent of the particle's composition. If we consider two coordinate systems S₁ and S₂, the first accelerating (in empty space) at a rate γ in the x direction, and the second at rest in a homogeneous gravitational field that imparts to all objects an acceleration of –γ in the x direction, then Einstein observed that

…as far as we know, the physical laws with respect to the S₁ system do not differ from those with respect to the S₂ system… we shall therefore assume the complete physical equivalence of a gravitational field and a corresponding acceleration of the reference system.

This was the beginning of Einstein’s search for an extension of the principle of relativity to arbitrary coordinate systems, and for a satisfactory relativistic theory of gravity, a search which ultimately led him to reject special relativity as a suitable framework in which to formulate the most fundamental physical laws.

Despite the importance that Einstein attached to the equivalence principle (even stating that the general theory of relativity “rests exclusively on this principle”), many subsequent authors have challenged its significance, and even its validity. For example, Ohanian and Rufinni (1994) emphatically assert that “gravitational effects are not equivalent to the effects arising from an observer's acceleration...", even limited to sufficiently small regions. In support of this assertion they describe how accelerometers “of arbitrarily small size” can detect tidal variations in a non-homogeneous gravitational field based on “local” measurements. Unfortunately they overlook the significance of their own comment regarding gradiometers, i.e., “the sensitivity attained depends on the integration time… with a typical integration time of 10 seconds the sensitivity demonstrated in a recent test was about the same as that of the Eotvos balance…”. Needless to say, the “locality” restriction refers to sufficiently small regions of spacetime, not just to small regions of space. The gradiometer may be only a fraction of a meter in spatial extent, but 10 seconds of temporal extent corresponds to three billion meters, which somewhat undermines the claim that the detection can be performed with such accuracy in an arbitrarily small region of spacetime.

The same kind of conceptual error appears in every example that purports to show the invalidity of the equivalence principle. For example, one well-known modern author points out that an arbitrarily small droplet of liquid, with zero surface tension, held together purely by its own gravitation, falling freely in the gravitational field of a spherical body will not be perfectly spherical, but will be slightly ellipsoidal, due to the tidal effects of the inhomogeneous field… and the shape does not approach sphericity as the radius of the droplet approaches zero. Furthermore, this applies to an arbitrarily brief “snapshot” of the falling droplet. He takes this to be proof of the falsity of the equivalence principle, but in fact it is just the opposite. If we began with a perfectly spherical droplet, it would take a significant amount of time traversing an inhomogeneous field for the shape to acquire its final ellipsoidal form, and as the length of time goes to zero, the deviation from sphericity also goes to zero. Likewise, once the droplet has acquired its ellipsoidal shape, this becomes its initial configuration upon entering any brief and small region of spacetime, and it exits from that region with the same shape, in perfect agreement with the equivalence principle, which tells us to expect all the parts of the droplet to maintain their initial mutual relations when in free fall.

Other authors have challenged the validity of the equivalence principle by considering the effects of rotation. Admittedly, a "sufficiently small" region of spacetime for transforming away the translatory motion of an object to some degree of approximation may not be sufficiently small for transforming away the rotational motion to the same degree of accuracy, but this does not conflict with the equivalence principle; it simply means that for an infinitesimal particle in a rotating body the "sufficiently small" region of spacetime is generally much smaller than for a particle in a non-rotating body, because it must be limited to a small arc of angular travel. In general, all such arguments against the validity of the (local) equivalence principle are misguided, based on a failure to correctly limit the extent of the subject region of space and time.

Others have argued that, although the equivalence principle is valid for infinitesimal regions of spacetime, this limitation renders it more or less meaningless. But this was answered by Einstein himself several times. For example, when the validity of the equivalence principle was challenged on the grounds that an arbitrary (inhomogeneous) gravitational field over some finite region cannot be “transformed away” by any single state of motion, Einstein replied

To achieve the essential equivalence of inertia and gravitation it is not necessary that the mechanical behavior of two or more masses must be explainable by the mere effect of inertia by the same choice of coordinates. After all, nobody denies, for example, that the theory of special relativity does justice to the nature of uniform motion, even though it cannot transform all acceleration-free bodies together to a state of rest by one and the same choice of coordinates.

This observation should have settled the matter, but unfortunately the same specious objection to the equivalence principle has been raised by successive generations of critics. This is ironic, considering a purely geometrical interpretation of gravity would clearly be impossible if gravitational and inertial acceleration were not intrinsically identical. The meaning of the equivalence principle (which Einstein called “the happiest thought of my life”) is that gravitation is not something that exists within spacetime, but is rather an attribute of spacetime. Inertial motion is just a special case of free-fall in a gravitational field. There is no additional entity or coupling present to produce the effects of gravity on a test body. Gravity is geometry. This may be expressed somewhat informally by saying that if we take sufficiently small pieces of curved and flat spacetime we can't tell one from the other, because they are the same stuff. The perfect equivalence between gravitational and inertial mass noted by Galileo implies that kinematic acceleration and the acceleration of gravity are intrinsically identical, and this makes possible a purely geometrical interpretation of gravity.

At the beginning of his 1916 paper on the foundations of the general theory of relativity, Einstein discussed “the need for an extension of the postulate of relativity”, and by considering the description of a physical object in terms of a rotating system of coordinates he explained why Euclidean geometry does not apply. This is the most common way of justifying the abandonment of Euclidean geometry, but in a paper written in 1914 Einstein gave a more elementary and (arguably) more profound reason for turning from Euclidean to Riemannian geometry. He pointed out that, prior to Faraday and Maxwell, the fundamental laws of physics contained finite distances, such as the distance r in Coulomb’s inverse-square law for the electric force F = q₁q₂/ r². Euclidean geometry is the appropriate framework in which to represent such laws, because it is an axiomatic structure based on finite distances, as can be seen from propositions such as the Pythagorean theorem r₁² = r₂² + r₃², where r₁, r₂, r₃ are the finite lengths of the edges of a right triangle. However, Einstein wrote

Since Maxwell, and by his work, physics has undergone a fundamental revision insofar as the demand gradually prevailed that distances of points at a finite range should not occur in the elementary laws, i.e., theories of “action at a distance” are now replaced by theories of “local action”. One forgot in this process that the Euclidean geometry too – as it is used in physics – consists of physical theorems that, from a physical aspect, are on an equal footing with the integral laws of Newtonian mechanics of points. In my opinion this is an inconsistent attitude of which we should free ourselves.

In other words, when “action at a distance” theories were replaced by “local action” theories, such as Maxwell’s differential equations for the electromagnetic field, in which only differentials of distance and time appear, we should have, for consistency, replaced the finite distances of Euclidean geometry with the differentials of Riemannian geometry. Thus the only valid form of the Pythagorean theorem is the differential form (ds)² = (dx)² + (dy)². Einstein then commented that it is rather unnatural, having taken this step, to insist that the coefficients of the squared differentials must be constant, i.e., that the Riemann-Christoffel curvature tensor must vanish. Hence we should regard Riemannian geometry rather than Euclidean geometry as the natural framework in which to formulate the elementary laws of physics.

From these considerations it follows rather directly that the influence of both inertia and gravitation on a particle should be expressed by the geodesic equations of motion

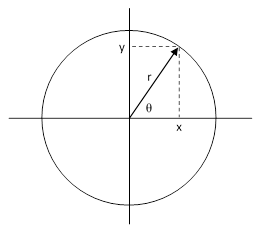
Einstein often spoke of the first term as representing the inertial part, and the second term, with the Christoffel symbols Γ^μ_αβ, as representing the gravitational field, and he was criticized for this, because the Christoffel symbols are not tensors, and they can be non-zero in perfectly flat spacetime simply by virtue of curvilinear coordinates. To illustrate, consider a flat plane with either Cartesian coordinates x,y or polar coordinates r,θ as shown below

With respect to the Cartesian coordinates we have the familiar Pythagorean line element (ds)² = (dx)² + (dy)². Also, since the polar coordinates are related to the Cartesian coordinates by the equations x = r cos(θ) and y = r sin(θ), we can evaluate the differentials

which are the transformation equations for the covariant metric tensor. Substituting these differentials into the Pythagorean metric equation, we have the metric for polar coordinates (ds)² = (dr)² + r² (dθ)². Therefore, the covariant and contravariant metric tensors for these polar coordinates are

and we have the determinant g = r². The only non-zero partial derivatives of the covariant metric components are  and , so the only non-zero Christoffel symbols are Γ^r_θθ = −r and Γ^θ_θr = Γ^θ_rθ = 1/r. Inserting these values into (1) gives the geodesic equations for this surface

Since we know this surface is a flat plane, the geodesic curves must be simply straight lines, and indeed it's clear from these equations that any purely radial path (for which dθ/ds = 0) is a geodesic. However, paths going "straight" in the θ direction (at constant r) are not geodesics, and these equations describe how the coordinates must vary along any given trajectory in order to maintain a geodesic path on the plane. If we insert these polar metric components into Gauss's curvature formula (discussed in Section 5.3) we get K = 0, consistent with the fact that the surface is flat. The reason the geodesics on this surface are not simple linear functions of the coordinates is not because the manifold is curved, but because the coordinates are curved. Hence we cannot absolutely identify the second term (or the Christoffel symbols) as the components of a gravitational field.

As early as 1916 Einstein was criticized for referring to the Christoffel symbols as the components of the gravitational. In response to a paper by Friedlich Kottler, Einstein wrote

Kottler censures that I interpret the second term in the equations of motion as an expression of the influence of the gravitational field upon the mass point, and the first term more or less as the expression of the Galilean inertia. Allegedly this would introduce real forces of the gravitational field and this would not comply with the spirit of the equivalence principle. My answer to this is that this equation as a whole is generally covariant, and therefore is quite in compliance with the hypothesis of covariance. The naming of the parts, which I have introduced, is in principle meaningless and only meant to appeal to our physical habit of thinking… that is why I introduced these quantities even though they do not have tensorial character. The principle of equivalence, however, is always satisfied when equations are covariant.

To some extent, Einstein side-stepped the criticism, because he actually did regard the Christoffel symbols as, in some sense, representing “true” gravity, even in flat spacetime. The "correct" classroom view today is that gravity is present only when intrinsic curvature is present, but it is actually not so easy to characterize the presence or absence of “gravity” in general relativity, especially because the flat metric of spacetime can be regarded as a special case of a gravitational field, rather than the absence of a gravitational field. This is the point of view that Einstein maintained throughout his life, to the consternation of some school teachers.

Consider again the flat two-dimensional space discussed above, and imagine some creatures living on a small region of this plane, and suppose they are under the impression that the constant-r and constant-θ loci are “straight”. They would have to conclude that the geodesic paths were curved, and that objects which naturally follow those paths are being influenced by some "force field". This is exactly analogous to someone in an upwardly accelerating elevator in empty space (i.e., far from any gravitating body). In terms of a coordinate system co-moving with the elevator, the natural paths of things are different than they would normally be, as if those objects were being influenced by an additional force field. This corresponds to the perceptions of the creatures on our flat plane, except that it is their θ axis which is non-linear, whereas our elevator's t axis is non-linear. Inside the accelerating elevator the additional tendency for geodesic paths to "veer off" is not really due to any extra non-linearity of the geodesics, it's due to the non-linearity of the elevator's coordinate system. Hence most people today would say that non-zero Christoffel symbols, by themselves, should not be regarded as indicative of the presence of "true" gravity. If the intrinsic curvature is zero, then non-vanishing Christoffel symbols simply represent the necessary compensation for non-linear coordinates, so, at most (the argument goes) they represent "pseudo-gravity" rather than “true gravity” in such circumstances.

But the distinction between “pseudo-gravity” and “true gravity” is precisely what Einstein denied. The equivalence principle asserts that these are intrinsically identical. Einstein’s point hasn't been fully appreciated by some subsequent writers of relativity text books. In a letter to his friend Max von Laue in 1950 he tried to explain:

...what characterizes the existence of a gravitational field from the empirical standpoint is the non-vanishing of the Γ^l_ik, not the non-vanishing of the [curvature]. If one does not think intuitively in such a way, one cannot grasp why something like a curvature should have anything at all to do with gravitation. In any case, no reasonable person would have hit upon such a thing. The key for the understanding of the equality of inertial and gravitational mass is missing.

The point of the equivalence principle is that curving coordinates are gravitation, and there is no intrinsic ontological difference between “true gravity” and “pseudo-gravity”. On a purely local (infinitesimal) basis, the phenomena of gravity and acceleration were, in Einstein's view, quite analogous to the electric and magnetic fields in the context of special relativity, i.e., they are two ways of looking at (or interpreting) the same thing, in terms of different coordinate systems. Now, it can be argued that there are clear physical differences between electricity and magnetism (e.g., no magnetic monopoles) and how they are "produced" by elementary particle "sources", but one of the keys to the success of special relativity was that it unified the electric and magnetic fields in free space without getting bogged down (as Lorentz did) in trying to fathom the ultimate constituency of elementary charged particles, etc. Likewise, general relativity unifies gravity and non-linear coordinates − including acceleration and polar coordinates − in free space, without getting bogged down in the "source" side of the equation, i.e., the fundamental nature of how gravity is ultimately "produced", why the elementary massive particles have the masses they have, and so on.

What Einstein was describing to von Laue was the conceptual necessity of identifying the purely geometrical effects of non-inertial coordinates with the physical phenomenon of gravitation. In contrast, the importance and conceptual significance of the curvature (as opposed to the connection) is mainly due to the fact that it defines the mode of coupling of the coordinates with the "source" side of the equation. Of course, since the effects of gravitation are reciprocal, all test particles are also sources of gravitation, and it can be argued that the equivalence principle is incomplete because it considers only the “passive” response of inertial mass points to a gravitational field, whereas a complete account must include the active participation of each mass point in the mutual production of the field. In view of this, it might seem to be a daunting task to attempt to found a viable theory of gravitation on the equivalence principle – just as it had seemed impossible to most 19th-century physicists that classical electrodynamics could proceed without determining the structure and self-action of the electron. But in both cases, almost miraculously, it turned out to be possible. On the other hand, as Einstein himself pointed out, the resulting theories were necessarily incomplete, precisely because they side-stepped the “source” aspect of the interactions.

Maxwell's theory of the electric field remained a torso, because it was unable to set up laws for the behaviour of electric density, without which there can, of course, be no such thing as an electro-magnetic field. Analogously the general theory of relativity furnished a field theory of gravitation, but no theory of the field-creating masses.

Return to Table of Contents