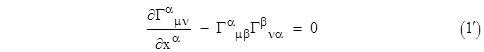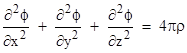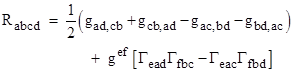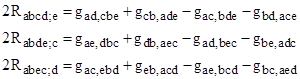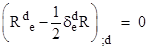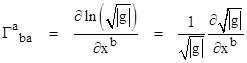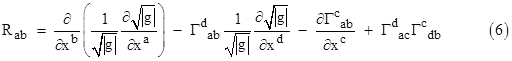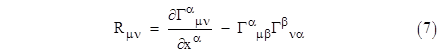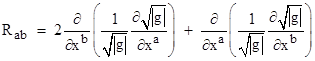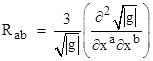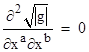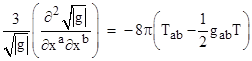The Field Equations

You told us how an almost churchlike atmosphere is pervading your desolate house now. And justifiably so, for unusual divine powers are at work in there.

                                                                  Besso to Einstein, 30 Oct 1915

The basis of Einstein's general theory of relativity is the audacious idea that not only do the metrical relations of spacetime deviate from perfect Euclidean flatness, but that the metric itself is a dynamical object. In every other field theory the equations describe the behavior of a physical field, such as the electric or magnetic field, within a constant and immutable arena of space and time, but the field equations of general relativity describe the behavior of space and time themselves. The spacetime metric is the field. This fact is so familiar that we may be inclined to simply accept it without reflecting on how ambitious it is, and how miraculous it is that such a theory is even possible, not to mention comprehensible. Spacetime plays a dual role in this theory, because it constitutes both the dynamical object and the context within which the dynamics are defined. This self-referential aspect gives general relativity certain characteristics different from any other field theory. For example, in other theories we formulate a Cauchy initial value problem by specifying the condition of the field everywhere at a given instant, and then use the field equations to determine the future evolution of the field. In contrast, because of the inherent self-referential quality of the metrical field, we are not free to specify arbitrary initial conditions, but only conditions that already satisfy certain self-consistency requirements (a system of differential relations called the Bianchi identities) imposed by the field equations themselves.

The self-referential quality of the metric field equations also manifests itself in their non-linearity. Under the laws of general relativity, every form of stress-energy gravitates, including gravitation itself. This is really unavoidable for a theory in which the metrical relations between entities determine the "positions" of those entities, and those positions in turn influence the metric. This non-linearity raises both practical and theoretical issues. From a practical standpoint, it ensures that exact analytical solutions will be very difficult to determine except in special cases. More importantly, from a conceptual standpoint, non-linearity ensures that the field cannot in general be uniquely defined by the distribution of material objects, because variations in the field itself can serve as "objects".

Furthermore, after eschewing the comfortable but naive principle of inertia as a suitable foundation for physics, Einstein concluded that "in the general theory of relativity, space and time cannot be defined in such a way that differences of the spatial coordinates can be directly measured by the unit measuring rod, or differences in the time coordinate by a standard clock...this requirement ... takes away from space and time the last remnant of physical objectivity". It seems that we're completely at sea, unable to even begin to formulate a definite solution, and lacking any definite system of reference for defining even the most rudimentary quantities. It's not obvious how a viable physical theory could emerge from such an austere level of abstraction.

These difficulties no doubt explain why Einstein's route to the field equations in the years 1907 to 1915 was so convoluted, with so much confusion and backtracking. One of the principles that heuristically guided his search was what he called the principle of general covariance. This was understood to mean that the laws of physics ought to be expressible in the form of tensor equations, because such equations automatically hold with respect to any system of curvilinear coordinates (within a given diffeomorphism class, as discussed in Section 9.2). He abandoned this principle at one stage, believing that he and Grossmann had proven it could not be made consistent with the Poisson equation of Newtonian gravitation, but he subsequently realized the invalidity of their arguments, and re-embraced general covariance as a fundamental principle.

It strikes many people as ironic that Einstein found the principle of general covariance to be so compelling, because, strictly speaking, it's possible to express almost any physical law, including Newton's laws, in generally covariant form (i.e., as tensor equations). This was not clear when Einstein first developed general relativity, but it was pointed out in one of the very first published critiques of Einstein's 1916 paper, and immediately acknowledged by Einstein. It's worth remembering that the generally covariant formalism had been developed only in 1901 by Ricci and Levi-Civita, and the first real use of it in physics was Einstein's formulation of general relativity. This historical accident made it natural for people (including Einstein, at first) to imagine that general relativity is distinguished from other theories by its general covariance, whereas in fact general covariance was only a new mathematical formalism, and does not connote a distinguishing physical attribute. For this reason, some people have been tempted to conclude that the requirement of general covariance is actually vacuous. In reply to this criticism, Einstein clarified the real meaning (for him) of this principle, pointing out that its heuristic value arises when combined with the idea that the laws of physics should not only be expressible as tensor equations, but should be expressible as simple tensor equations. In 1918 he wrote "Of two theoretical systems which agree with experience, that one is to be preferred which from the point of view of the absolute differential calculus is the simplest and most transparent". This is still a bit vague, but it seems that the quality which Einstein had in mind was closely related to the Machian idea that the expression of the dynamical laws of a theory should be symmetrical up to arbitrary continuous transformations of the spacetime coordinates. Of course, the presence of any particle of matter with a definite state of motion automatically breaks the symmetry, but a particle of matter is a dynamical object of the theory. The general principle that Einstein had in mind was that only dynamical objects could be allowed to introduce asymmetries. This leads naturally to the conclusion that the coefficients of the spacetime metric itself must be dynamical elements of the theory, i.e., must be acted upon. In this way, Einstein believed he had addressed what he regarded as the strongest of Mach's criticisms of Newtonian spacetime, namely, the fact that Newton's space acted on objects but was never acted upon by objects.

Let's follow Einstein's original presentation in his famous paper "The Foundation of the General Theory of Relativity", which was published early in 1916. He notes that for empty space, far from any gravitating object, we expect to have flat (i.e., Minkowskian) spacetime, which amounts to requiring that Riemann's curvature tensor R_abcd vanishes. However, in regions of space near gravitating matter we must clearly have non-zero intrinsic curvature, because the gravitational field of an object cannot simply be "transformed away" (to the second order) by a change of coordinates. Thus there is no system of coordinates with respect to which the manifold is flat to the second order, which is precisely the condition indicated by a non-vanishing Riemann curvature tensor. Nevertheless, even at points where the full curvature tensor R_abcd is non-zero, the contracted tensor of the second rank, R_bc= g^adR_abcd = R^d_bcd may vanish. Now, a tensor of rank four can be contracted in six different ways (the number of ways of choosing two of the four indices), and in general this gives six distinct tensors of rank two. We are able to single out a more or less unique contraction of the curvature tensor only because of that tensor’s symmetries (described in Section 5.7), which imply that of the six contractions of R_abcd, two are zero and the other four are identical up to sign change. Specifically we have

By convention we define the Ricci tensor R_bc as the contraction g^adR_abcd. In seeking suitable conditions for the metric field in empty space, Einstein observes that

…there is only a minimum arbitrariness in the choice... for besides R_μν there is no tensor of the second rank which is formed from the g_μν and it derivatives, contains no derivative higher than the second, and is linear in these derivatives… This prompts us to require for the matter-free gravitational field that the symmetrical tensor R_μν ... shall vanish.

Thus, guided by the belief that the laws of physics should be the simplest possible tensor equations (to ensure general covariance), he proposes that the field equations for the gravitational field in empty space should be

Noting that R_μν takes on a particularly simple form on the condition that we choose coordinates such that = 1, Einstein originally expressed this in terms of the Christoffel symbols as

(In his 1916 paper Einstein had a different sign because he defined the symbol Γ^a_bc as the negative of the Christoffel symbol of the second kind.) He then concludes the section with words that obviously gave him great satisfaction, since he repeated essentially the same comments at the conclusion of the paper:

These equations, which proceed, by the method of pure mathematics, from the requirement of the general theory of relativity, give us, in combination with the [geodesic] equations of motion, to a first approximation Newton's law of attraction, and to a second approximation the explanation of the motion of the perihelion of the planet Mercury discovered by Leverrier. These facts must, in my opinion, be taken as a convincing proof of the correctness of the theory.

To his friend Paul Ehrenfest in January 1916 he wrote that "for a few days I was beside myself with joyous excitement", and to Fokker he said that seeing the anomaly in Mercury's orbit emerge naturally from his purely geometrical field equations "had given him palpitations of the heart". (These recollections are remarkably similar to the presumably apocryphal story of Newton's trembling hand when he learned, in 1675, of Picard's revised estimates of the Earth's size, and was thereby able to reconcile his previous calculations of the Moon's orbit based on the assumption of an inverse-square law of gravitation.)

The expression R_μν = 0 represents ten distinct equations in the ten unknown metric components g_μν at each point in empty spacetime (where the term "empty" signifies the absence of matter or electromagnetic energy, but obviously not the absence of the metric/gravitational field.) Since these equations are generally covariant, it follows that given any single solution we can construct infinitely many others simply by applying arbitrary (continuous) coordinate transformations. Thus, each individual physical solution has four full degrees of freedom which allow it to be expressed in different ways. In order to uniquely determine a particular solution we must impose four coordinate conditions on the g_μν, but this gives us a total of fourteen equations in just ten unknowns, which could not be expected to possess any non-trivial solutions at all if the fourteen equations were fully independent and arbitrary. Our only hope is if the ten formal conditions represented by our basic field equations automatically satisfy four identities for any values of the metric components, so that they really only impose six independent conditions, which then would uniquely determine a solution when augmented by a set of four arbitrary coordinate conditions.

It isn't hard to guess that the four "automatic" conditions to be satisfied by our field equations must be the vanishing of the covariant derivatives (see Appendix 4), since this will guarantee local conservation of any energy-momentum source term that we may place on the right side of the equation, analogous to the mass density on the right side of Poisson's equation

where we’ve chosen units so that Newton’s gravitational constant equals 1. In tensor calculus the divergence generalizes to the covariant derivative, so we expect that the covariant derivatives of the metrical field equations must identically vanish. The Ricci tensor R_μν itself does not satisfy this requirement, but we can create a tensor that does satisfy the requirement (using the Bianchi identity as explained below) with just a slight modification of the Ricci tensor, and without disturbing the relation R_μν = 0 for empty space. Subtracting half the metric tensor times the invariant R = g^μνR_μν gives what is now called the Einstein Tensor

Obviously the condition R_μν = 0 implies G_μν = 0. Conversely, if G_μν = 0 we can see from the mixed form

that R must be zero, because otherwise R_μν would need to be diagonal, with the components R/2, which doesn't contract to the scalar R (except in two dimensions). Consequently, the condition G_μν = 0 is equivalent to R_μν = 0 for empty space, but for coupling with a non-zero source term we must use G_μν to represent the metrical field.

To represent the "source term" we will use the covariant energy-momentum tensor T_μν, and regard it as the "cause" of the metric curvature (although one might also conceive of the metric curvature as, in some temporally symmetrical sense, "causing" the energy-momentum). The components of this symmetrical tensor are the fluxes of the four components of momentum in each of the four directions. Thus the time-time component T₀₀ is the mass-energy density, T_0j are the translational momenta, and the remaining T_jk are momentum fluxes signifying pressures and shear stresses. (For this reason, T_μν is sometimes called the stress-energy tensor.)

Einstein acknowledged that the introduction of this tensor is not justified by the relativity principle alone, but it has the virtues of being closely related by analogy with the Poisson equation from Newton's theory, it gives local conservation of energy and momentum, and finally it implies gravitational energy gravitates just as does every other form of energy. On this basis we surmise that the field equations coupled to the source term can be written in the form G_μν = κT_μν where κ is a constant which must equal −8π (remembering that Newton's gravitational constant is 1 in our units) in order for the field equations to reduce to Newton's law in the weak field limit. Thus we have the complete expression of Einstein's metrical law of general relativity

The minus sign of the right hand side is due to our choice of g^adR_abcd for the definition of the Ricci tensor. As noted above, this is the negative of g^acR_abcd, which we could just as well have chosen as the definition of the Ricci tensor, in which case the sign of the right side of (2) would be positive. The choice is purely conventional.

It's worth noting that although the left side of the field equations is quite pure and almost uniquely determined by mathematical requirements, the right side is a hodge-podge of miscellaneous "stuff". As Einstein wrote,

The energy tensor can be regarded only as a provisional means of representing matter. In reality, matter consists of electrically charged particles... It is only the circumstance that we have no sufficient knowledge of the electromagnetic field of concentrated charges that compels us, provisionally, to leave undetermined in presenting the theory, the true form of this tensor... The right hand side [of (2)] is a formal condensation of all things whose comprehension in the sense of a field theory is still problematic. Not for a moment... did I doubt that this formulation was merely a makeshift in order to give the general principle of relativity a preliminary closed-form expression. For it was essentially no more than a theory of the gravitational field, which was isolated somewhat artificially from a total field of as yet unknown structure.

Alas, neither Einstein nor anyone since has been able to make further progress in determining the true form of the right hand side of (2), although it is at the heart of current efforts to reconcile quantum field theory with general relativity. At present we must be content to let T_μν represent, in a vague sort of way, the energy density of the electromagnetic field and matter.

A different (but equivalent) form of the field equations can be found by contracting (2) with g^μν to give R – 2R = –R = –8πT, and then substituting for R in (2) to give

which again makes clear that the field equations for empty space are simply R_μν = 0.

Incidentally, the tensor G_μν was named for Einstein because of his inspired use of it, not because he discovered it. Indeed the vanishing of the covariant derivative (see Appendix 4) of this tensor had been discovered by Aurel Voss in 1880, by Ricci in 1889, and again by Luigi Bianchi in 1902, all apparently independently. Bianchi had once been a student of Felix Klein, so it's not surprising that Klein was able in 1918 to point out regarding the conservation laws in Einstein's theory of gravitation that we need only "make use of the most elementary formulae in the calculus of variations". Recall from Section 5.7 that the Riemann curvature tensor in terms of arbitrary coordinates is

At the origin of Riemann normal coordinates this reduces to R_abcd = g_ad,cb – g_ac,bd , because in such coordinates the Christoffel symbols are all zero and we have the special symmetry g_ab,cd = g_cd,ab. Now, if we consider partial derivatives (which in these special coordinates are equal to the covariant derivatives) of this tensor, we see that the derivative of the quantity in square brackets still vanishes, because the product rule implies that each term is a Christoffel symbol times the derivative of a Christoffel symbol. We might also be tempted to take advantage of the special symmetry g_ab,cd = g_cd,ab , but this is not permissible because although the two quantities are equal (at the origin of Riemann normal coordinates), their derivatives are not generally equal. Hence when evaluating the derivatives of the Riemann tensor, even at the origin of Riemann normal coordinates, we must consider all four of the metric tensor derivatives in the above expression. Denoting covariant differentiation with respect to a coordinate x^m by the subscript ;m, we have

Noting that partial differentiation is commutative, and the metric tensor is symmetrical, we see that the sum of these three tensors vanishes at the origin of Riemann normal coordinates, and therefore with respect to all coordinates. Thus we have the Bianchi identities

Multiplying through by g^adg^bc , making use of the symmetries of the Riemann tensor, and the fact that the covariant derivative of the metric tensor vanishes identically, we have

which reduces to

Thus we have

showing that the "divergence" of the tensor inside the parentheses (the Einstein tensor) vanishes identically.

One outcome of the struggle to understand the conservation laws of the relativistic field equations was Emmy Noether’s famous theorem on the relation between symmetries and conservation laws. Also, Klein explored how general relativity embodies some aspects of his Erlangen program.

A slight (but significant) extension of the field equations was proposed by Einstein in 1917 based on cosmological considerations, as a means of ensuring stability of a static closed universe. To accomplish this, he introduced a linear term with the cosmological constant λ as follows

When Hubble and other astronomers began to find evidence that in fact the large-scale universe is expanding, and Einstein realized his ingenious introduction of the cosmological constant had led him away from making such a fantastic prediction, he called it (according to George Gamow) "the biggest blunder of my life”.

It's worth noting that Einsteinian gravity is possible only in four dimensions, because in any fewer dimensions the vanishing of the Ricci tensor R_μν implies the vanishing of the full Riemann tensor, which means no curvature and therefore no gravity in empty space. Of course, the actual field equations for the vacuum assert that the Einstein tensor (not the Ricci tensor) vanishes, so we should consider the possibility of G being zero while R is non-zero. We saw above that G = 0 implies R = 0, but that was based on the assumption of a four-dimensional manifold. In general for an n-dimensional manifold we have R – (n/2)R = G, so if n is not equal to 2, and if G_μν vanishes, we have G = 0 and it follows that R = 0, and therefore R_μν must vanish. However, if n = 2 it is possible for G to equal zero even though R is non-zero. Thus, in two dimensions, the vanishing of G_μν does not imply the vanishing of R_μν. In this case we have

where λ can be any constant. Multiplying through by g_μν gives

This is the vacuum solution of Einstein's field equations in two dimensions. This is also the vacuum solution for the field equations in four dimensions if λ is identified as the non-zero cosmological constant. Any space of constant curvature is of this form, although a space of this form need not be of constant curvature.

Once the field equations have been solved and the metric coefficients have been determined, we then compute the paths of objects by means of the equations of motion. It was originally taken as an axiom that the equations of motion are the geodesic equations of the manifold, but in a series of papers from 1927 to 1949 Einstein and others showed that if particles are treated as singularities in the field, then they must propagate along geodesic paths. Therefore, it is not necessary to make an independent assumption about the equations of motion. This is one of the most remarkable features of Einstein's field equations, and is possible only because of the non-linear nature of the equations. Of course, the hypothesis that particles can be treated as field singularities may seem no more intuitively obvious than the geodesic hypothesis itself. Indeed Einstein himself was usually very opposed to admitting any singularities, so it is somewhat ironic that he took this approach to deriving the equations of motion. On the other hand, in 1939 Fock showed that the field equations imply geodesic paths for any sufficiently small bodies with negligible self-gravity, not treating them as singularities in the field. This approach also suggests that more massive bodies would deviate from geodesics, and it relies on representing matter by the stress-energy tensor, which Einstein always viewed as only a provisional formal expression.

To appreciate the physical significance of the Ricci tensor it's important to be aware of a relation between the contracted Christoffel symbol and the scale factor of the fundamental volume element of the manifold. This relation is based on the fact that if the square matrix A is the inverse of the square matrix B, then the components of A can be expressed in terms of the components of B by the equation A_ij = (∂B/∂B_ij)/B where B is the determinant of B. Accordingly, since the covariant metric tensor g_μν and the contravariant metric tensor g^μν are matrix inverses of each other, we have

where g is the determinant of g_μν. If we multiply both sides by the partial of g_μν with respect to the coordinate x^α we have

Notice that the left hand side looks like part of a Christoffel symbol. Recall the general form of these symbols

If we set one of the lower indices of the Christoffel symbol, say c, equal to a, then we have the contracted symbol

Since the indices a and σ are both dummies (meaning they each take on all possible values in the implied summation), and since g^aσ = g^σa, we can swap a and σ in any of the terms without affecting the result. Swapping a and σ in the last term inside the parentheses we see it cancels with the first term, and we're left with

Comparing this with our previous result (4), we find that the contracted Christoffel symbol can be written in the form

Furthermore, recalling the elementary fact that the derivative of ln(y) equals 1/y times the derivative of y, and the fact that k ln(y) = ln(y^k), this result can also be written in the form

Since our metrics all have negative determinants, we can replace |g| with −g in these expressions. We're now in a position to evaluate the geometrical and physical significance of the Ricci tensor, the vanishing of which constitutes Einstein's vacuum field equations. The general form of the Ricci tensor is

which of course is a contraction of the full Riemann curvature tensor. Making use of the preceding identity, this can be written as

In his original 1916 paper on the general theory Einstein initially selected coordinates such that the metric determinant g was a constant −1, in which case the partial derivatives of  all vanish and the Ricci tensor is simply

The vanishing of this tensor constitutes Einstein's vacuum field equations (1'), provided the coordinates are such that g is constant. (These field equations can also be derived from a variational principle, taking the Ricci scalar R as the Hamiltonian function, as discussed in Appendix 5.) Even if g is not constant in terms of the natural coordinates, it is often possible to transform the coordinates so as to make g constant. For example, Schwarzschild replaced the usual r and θ coordinates with x = r³/3 and y = –cos(θ), together with the assumption that g_tt = 1/g_rr, and thereby expressed the spherically symmetrical line element in a form with g = −1.  It is especially natural to impose the condition of constant g in static systems of coordinates and spatially uniform fields. We spend most of our time suspended quasi-statically in a nearly uniform gravitational field, so we are most intuitively familiar with gravity in this form. From this point of view we identify the effects of gravity with the geodesic accelerations relative to our static coordinates, as represented by the Christoffel symbols. Indeed Einstein admitted that he conceptually identified the gravitational field with the Christoffel symbols, despite the fact that it's possible to have non-vanishing Christoffel symbols in flat spacetime, as discussed in Section 5.6

However, we can also take the opposite view. Rather than focusing on "stationary" coordinate systems with constant metric determinants which make the first two terms of (6) vanish, we can focus on "free-falling" inertial coordinates (also known as Riemann normal coordinates) in terms of which the Christoffel symbols, and therefore the second and fourth terms of (6), vanish at the origin. In other words, we "abstract away" the original sense of gravity as the extrinsic acceleration relative to some physically distinguished system of stationary coordinates (e.g., Schwarzschild coordinates), and focus instead on the intrinsic tidal accelerations (i.e., local geodesic deviations) that correspond to the intrinsic curvature of the manifold. At the origin of Riemann normal coordinates the Ricci tensor (5) reduces to

where, as usual, subscripts following commas signify partial derivatives with respect to the designated coordinate. Making use of the skew symmetry on the lower three indices of the Christoffel symbol partial derivatives in these coordinates (as described in Section 5.7), the second term on the right hand side can be replaced with the negative of its two complementary terms given by rotating the lower indices, so we have

Noting that each of the three terms on the right side is now a partial derivative of a contracted Christoffel symbol, we have

At the origin of Riemann normal coordinates the first partial derivatives of g, and therefore of 1/√|g|, all vanish, so the chain rule allows us to bring those factors outside the differentiations, and noting the commutativity of partial differentiation we arrive at the expression for the components of the Ricci tensor at the origin of Riemann normal coordinates

The quantity √|g| is essentially a scale factor for the incremental 4-volume element dV, which is to say

Therefore, at the origin of Riemann normal (free-falling inertial) coordinates the components of the Ricci tensor R_ab are three times the second derivatives of the 4-volume scale factor divided by that scale factor itself. The vacuum field equations R_ab = 0 express the vanishing of these second derivatives with respect to any two coordinates (not necessarily distinct), i.e.,

Since the 4-volume scale factor is not changing, it can be shown that a geodesic sphere (e.g., a small shell of free-falling dust particles initially at rest with respect to each other) does not change it's volume during an incremental advance of proper time. Of course, this doesn't give a complete description of the effects of gravity in vacuum, in part because it doesn’t describe how these local Riemann normal coordinates are related to some stationary system of coordinates (which we typically use to describe events), and in part because although the volume of the sphere isn't changing at this instant, its shape may gradually change due to tidal acceleration. In some small region located in a spherically symmetrical field, the cloud will become lengthened in the radial direction and shortened in the normal directions. This variation in the shape is characterized by the Weyl tensor, which in general may be non-zero even when the Ricci tensor vanishes.

For locations where there is non-zero energy-momentum, the "complete" field equations in the form of (3), when expressed in Riemann normal coordinates, are

which signifies that, at any given event, three times the second derivatives of the 4-volume scale factor, divided by the scale factor, equal the corresponding components of the "divergence-free" energy-momentum tensor (expressed by the right hand side) at that event. In many circumstances the time-time equation (a = b = 0) is predominant, and noting that T₀₀ = ρ (the mass-energy density) and T₁₁ = P_x, etc., (the pressures), we have R₀₀ = –4π(ρ + P_x + P_y + P_z).

The variation of the scale factor causes geodesics to deviate from (non-radial) normal coordinate lines. For deviations σ^a normal to a vector in the time direction we have d²σ^a/dτ² = R^a_0b0 σ^b, so the average over radial vectors with incremental length r in the four basis directions is d²r/dτ² = R₀₀ r/4 (recalling our sign convention for the Ricci tensor). Also, since the 4-volume V is proportional to r⁴, at an initial static condition we have (1/V)d²V/dτ² = R₀₀, which equals –4π(ρ+3P) with isotropic pressure P. This refers to the 4-volume, but in this context it can be shown to apply to the spatial 3-volume as well. Thus the volume of a small geodesic 3-sphere contracts with an acceleration proportional to the enclosed mass-energy density and pressures. When the pressure is negligible this corresponds to the Newtonian relation (1/V)d²V/dt² = –4πρ.

It may seem that focusing purely on the volume effect of gravitation in free-falling normal coordinates ignores what is usually the most physically obvious manifestation of gravity, namely, the tendency of objects to "fall down", i.e., the acceleration of the geodesics relative to our usual static coordinates near a gravitating body. However, in most cases this too can be viewed as volume effects, provided we take a wider view of events. For example, the fall of a single apple to the ground at one location on Earth can be transformed away (locally) by a suitable system of accelerating coordinates, but the fall of apples all over the Earth cannot. In effect these apples can be seen as a spherical cloud of dust particles, each following a geodesic path, and those paths are converging and the cloud's volume is shrinking at an accelerating rate as the shell collapses toward the Earth. The rate of acceleration (i.e., the second derivative with respect to time) is proportional to the mass-energy (and pressures) of the Earth, in accord with the field equations.

Return to Table of Contents