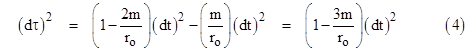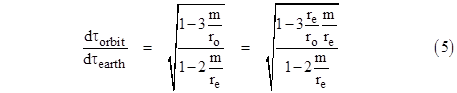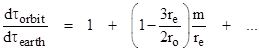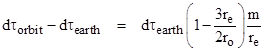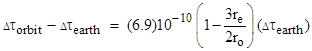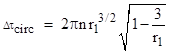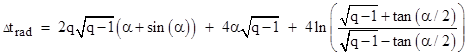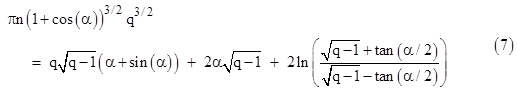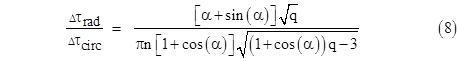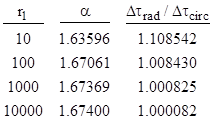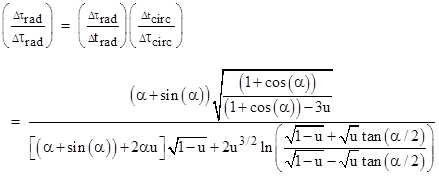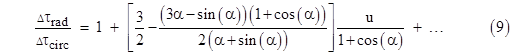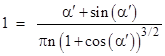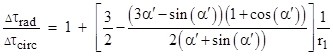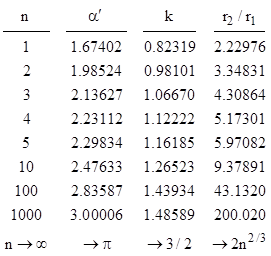6.5  Proper Time for Intersecting Orbits

Time is the longest distance between two places.

                                                Tennessee Williams, 1945

The lapse of proper time for moving clocks in a gravitational field is often computed by splitting the problem into separate components, one to account for the velocity effect in accord with special relativity, and another to account for the gravitational effect in accord with general relativity. However, the general theory subsumes the special theory, and it's usually easier to treat such problems holistically from a purely general relativistic standpoint. (The persistent tendency to artificially bifurcate problems into "special" and "general" components is partly due to the historical accident that Einstein arrived at the final theory in two stages.)

The spacetime metric in the vicinity of a non-rotating spherical body of mass m in terms of Schwarzschild coordinates is given by equation (3) in Section 6.1. For a stationary position on the surface of such a body of radius r, the radial and angular differentials are all zero, and the relationship between the proper time t and the Schwarzschild coordinate time t can be read directly from the metric as

On the other hand, the equations of motion for a general orbital path in the equatorial plane were derived in Section 6.2. If we differentiate equation (10) of that section with respect to τ, divide through by 2(dr/dτ), and recall that h = ωr² where ω = dϕ/dτ, we have

For a circular orbit of constant radius r this gives the relativistic form of Kepler’s third law

which can also be written as m = ω²r³/(1+3ω²r²). This may seem inconsistent with the claim in Section 5.5 that Kepler's law m = ω²r³ holds exactly in general relativity, but recall that we defined ω in that section as df/dt, i.e., the derivative of ϕ with respect to Schwarzschild coordinate time, rather than the proper time. Thus, for a circular orbit of radius r, Kepler’s law does indeed imply r² = m/(ω²r) = (dt/dϕ)²(m/r), which we can substitute for the coefficient of (dϕ)² in the metric to show that the proper time and Schwarzschild coordinate time along the path of a particle in a circular orbit of radius r satisfies

Now for two test particles, one sitting stationary at the North Pole at a distance r_e from the center of the Earth (assumed spherical), and one in a circular orbit of radius r_o, we can combine equations (1) and (4) to give the ratio of the orbital proper time to the North Pole's proper time as

To isolate the difference in the two proper times, we can expand the above function into a power series in m/r to give

Multiplying through by dτ_earth and then subtracting this quantity from both sides, we get

The mass of the earth in geometrical units is about m = 0.00443 meters, and the radius of the earth is about r_e = 6.378(10)⁶ meters, so we can insert these values and integrate over a given lapse Δτ_earth of proper time measured on Earth to give the difference between this elapsed time and the corresponding elapsed time for the circular orbit

Consequently, for an orbit at the radius r_o = (3/2)r_e (about 2000 miles up) there is no difference in the lapses of proper time. For orbits lower than 3r_e/2 the satellite will show slightly less lapse of proper time (i.e., the above discrepancy will be negative), whereas for higher orbits it will show slightly more elapsed time than the corresponding interval at the North Pole. One might think that a further adjustment would be necessary to correlate the elapsed time to a particle at rest on the equator, to account for the rotation of the Earth, but the Earth tends to bulge due to its rotation in such a way that it maintains roughly an equi-potential surface, meaning that the rate of proper time is approximately constant at sea level, regardless of latitude. Indeed this was the basis of Newton’s prediction of the Earth’s oblate shape, since (as he pointed out) if the surface of the seas was not equi-potential, the water would flow so as to achieve equilibrium.

In a low Earth orbit of, say, 254 miles, we have r_e/r_o = 0.9396, so the proper time runs about 24.6 microseconds per day slower than a clock on the Earth. On the other hand, for a geo-synchronous orbital radius of 42164 kilometers we have r_e/r_o = 0.151, so the orbit's lapse of proper time actually exceeds the corresponding lapse of proper time on Earth by about 46.4 microseconds per day. Of course, as r_o continues to increase, the orbital velocity drops to zero and we are left with just coordinate time for the orbit, relative to which a clock on Earth is "running slow" by about 60 micro-seconds per day, due entirely to the gravitational potential of the earth. (Hence during a typical human life span the Earth's gravity stretches out our lives to cover an extra 1.57 seconds of coordinate time.) Of particular interest is the orbit of the Global Positioning System (GPS) satellites, which are located in circular orbits approximately 20200 kilometers above the Earth’s surface (not a geosynchronous orbit, as is sometimes thought). It follows that the orbital radius of the GPS satellites is R = 20200+6378 = 26578 kilometers, giving a ratio r_o/r_e of about 4.2. Inserting this ratio into the above formula, we find that the elapsed proper time per Earth-day for a GPS satellite is about 38.1 micro-seconds more than the elapsed time on the surface of the Earth.

Incidentally, the value of τ_orbit given by equation (5) goes to zero when the orbital radius r_o equals 3m, consistent with the fact that 3m is the radius of the orbit of light. This suggests that even if something prevented a massive object from collapsing within its Schwarzschild radius 2m, it would still be a very remarkable object if it was just within 3m, because then it could (theoretically) support circular light orbits, although such orbits would not be stable (even neglecting interference from in-falling matter). If neutrinos were massless there could also be neutrinos in 3m (unstable) orbits near such an object, but the evidence today indicates that neutrinos have a small positive mass.

The results of this and the previous section can be used to clarify the so-called twins paradox. In some treatments of special relativity the difference between the elapsed proper times along different paths between two fixed events is attributed to a difference in the locally "felt" accelerations along those paths. In other words, it is said that the twins in their separate capsules cannot be surprised at their asymmetric ages upon re-uniting, because one has experienced acceleration and the other has not. However, this explanation fails in the context of general relativity and gravity, because there exist multiple free-fall (i.e., locally unaccelerated) paths of different proper lengths connecting two fixed events. This occurs, for example, with any two intersecting orbits with different eccentricities, provided they are arranged so that the clocks coincide at two intersections.

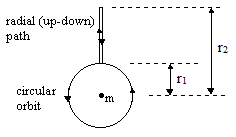
To illustrate, consider the intersections between a circular and a purely radial “orbit” in the gravitational field of a spherically symmetrical mass m. One clock follows a perfectly circular orbit of radius r, while the other follows a purely radial (up and down) trajectory, beginning at a height r₁, climbing to r₂, and falling back to r₁, as shown below.

We can arrange for the two clocks to initially coincide, and for the first clock to complete n circular orbits in the same (coordinate) time it takes for the second clock to rise and fall. Thus the objects coincide at two fixed events, and they are each in free-fall continuously between those two events. Nevertheless, we will see that the elapsed proper times for these two objects are not the same.

Throughout this example, we will use dimensionless times and distances by dividing each quantity by the central mass m in geometric units. For a circular orbit of radius r in Schwarzschild coordinates, we can integrate Kepler's third law to give the coordinate time to complete n revolutions

Applying the constant ratio of proper time to coordinate time for a circular orbit, we also have the proper time to complete n revolutions

For the radially moving object the usual parametric cycloid relation (see Section 6.4) gives the total proper time for the rise and fall

where q = r₂/2 and the parameter α satisfies the relation

The total elapsed coordinate time for this radial path is

In order for the objects to coincide at the two events, the coordinate times must be equal, i.e., we must have Δt_circ = Δt_rad. Therefore, replacing r₁ with (1+cos(α))q in the expression for the coordinate time in circular orbits, we find that for any given n and q (= r₂/2) the parameter α must satisfy

For any given values of q and n we can solve this equation for α, and then determine the ratio of the elapsed proper times for the two paths from the relation

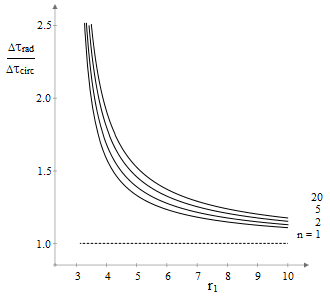
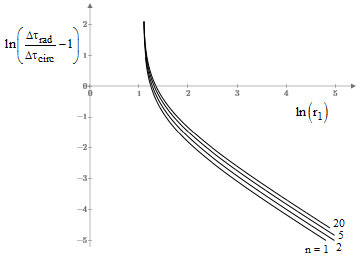
With n = 1, 2, 5, and 20 the ratio of proper times for a range of fairly small values of r₁ (as a dimensionless ratio of the mass m) behaves as shown below.

Not surprisingly, the ratio goes to infinity as r₁ drops to 3m, because the proper time for a circular orbit of radius 3m is zero. The α parameters and proper time ratios for some larger values of r with n = 1 are tabulated below.

The asymptotic behavior as r₁ (as a dimensionless ratio of m) increases can be seen in the logarithmic plot below for various values of n.

To determine the asymptotic behavior for large values of r₁, recall that Δt_circ = Δt_rad, so we can write the ratio of proper times as the product of the ratios of proper and coordinate times for radial and circular paths. Thus, making the substitution q = 1/u, and multiplying through the numerator and denominator by u^3/2, the ratio of proper times can be written in terms of the small parameter u as

Expanding this into a series to the first order in u we get

In order for the paths to intersect for a given value of n, we must set α to the appropriate value, namely, the asymptotic value for any given value of n as q approaches infinity. Letting αʹ denote this asymptotic value, in view of (8) we see that the value of αʹ satisfies the relation

Making the substitution u = (1+cos(α))/r₁ and inserting αʹ into equation (9), we get the asymptotic ratio of proper times for intersecting radial and circular orbits for large values of r₁

Letting k denote the coefficient of 1/r₁ in this equation, the values of αʹ, k, and r₂/r₁ are as given in the table below for various values of n.

As expected, k approaches 3/2 as n increases, because in that case the radial path is mostly very slow and distant, so its proper time is nearly coordinate time, and hence the ratio of proper times is given by equation (4), which implies k = 3/2.

As an example, consider a clock in a circular orbit at 360 miles above the Earth's surface. In this case the radius of the orbit is about (6.957)10⁶ meters. Since the mass of the Earth in geometrical units is 0.00443 meters, we have the normalized radius r₁ = (1.57053)10⁹, and the total time of one orbit is approximately 5775 seconds (i.e., about 1.604 hours). For a radial trajectory to begin and end at this altitude and have the same elapsed coordinate time as one circular orbit at this altitude, the radial trajectory must extend up to r₂ = (1.55)10⁷ meters, which is about 5698 miles above the Earth's surface. Taking k from the table with n = 1, we have

and so the difference in elapsed proper times is given by

This is the amount by which the elapsed time on the radial (up-down) path would exceed the elapsed time on the circular path.

Return to Table of Contents