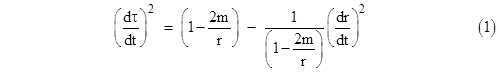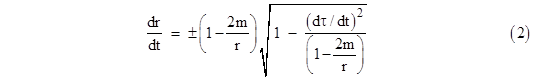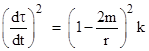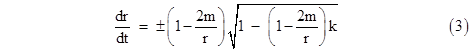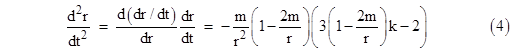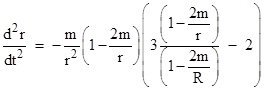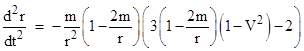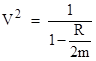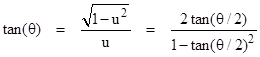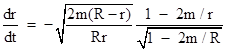6.7  Gravitational Acceleration in Schwarzschild Coordinates

If bodies, moved in any manner among themselves, are urged in the direction of parallel lines by equal accelerative forces, they will all continue to move among themselves, after the same manner as if they had not been urged by those forces.

                                                                                                      Isaac Newton, 1687

According to Newton's theory the acceleration of gravity of a test particle at a given radial distance from a large mass is independent of the particle’s state of motion. Consequently it would be impossible to tell, from the relative motions of a group of free-falling test particles in a small region of space, that those particles were subject to any force. Maxwell emphasized the same point when he wrote (in the posthumously published “Matter and Motion”) that acceleration is relative, because only the differences between the accelerations of bodies can be detected.

Our whole progress up to this point may be described as a gradual development of the doctrine of relativity of all physical phenomena... There are no landmarks in space; one portion of space is exactly like every other portion, so that we cannot tell where we are. We are, as it were, on an unruffled sea, without stars, compass, soundings, wind, or tide, and we cannot tell in what direction we are going. We have no log which we can cast out to take a dead reckoning by; we may compute our rate of motion with respect to the neighbouring bodies, but we do not know how these bodies may be moving in space. We cannot even tell what force may be acting on us; we can only tell the difference between the force acting on one thing and that acting on another.

Of course, he was referring here to forces (such as gravity) that are proportional to inertial mass, so they impart equal accelerations to every body. As an example of a localized set of bodies subjected to equal acceleration, he considered ordinary objects on the earth’s surface, all of which are subjected (along with the earth itself) to the sun’s gravitational force and the corresponding acceleration. He noted that if this were not the case, i.e., if the sun’s gravity attracted only the earth but not ordinary small objects on the earth’s surface, this would be easily detectable by (for instance) changes in the position of a plumb line between sunrise and sunset.

Naturally these facts are closely related to the equivalence principle, but there are some subtle differences when we consider the accelerations of bodies due to gravity in the context of general relativity. We saw in Section 6.4 that the second derivative of r with respect to the proper time τ of a radially moving free particle in general relativity is simply

and thus independent of the particle’s state of motion, just as with Newtonian gravity. However, this formal similarity must be treated carefully, because of the distinction between Newtonian time and the different concepts of time in general relativity. To illustrate, recall that Kepler’s third law in general relativity is m = ω²r³, which is formally identical to the Newtonian law, but only if ω is defined as dϕ/dt. If, on the other hand, we define ω = dϕ/dτ, then we can differentiate equation (10) of Section 6.2 with respect to τ, divide through by 2(dr/dτ), and recall that h = ωr², to give

This implies, for a circular orbit, that m = ω²r³(1–3m/r), which can also be written as m = ω²r³/(1+3ω²r²). Thus the form of Kepler’s law is different, depending on whether we define ω as the derivative of ϕ with respect to Schwarzschild coordinate time or proper time.

Similarly, the expression for the radial acceleration of gravity depends on whether the derivatives are taken with respect to coordinate time or proper time. The proper times of two (momentarily) coincident particles may differ depending on their states of motion, so when we consider the motions of such particles in terms of a common system of coordinates the result will not be as simple as the Newtonian expression. The second derivative of the radial coordinate r with respect to the time coordinate t in terms of the usual Schwarzschild coordinates depends not only on the spacetime location of the particle (i.e., r and t) but also on the trajectory of the particle through that point, even for particles with purely radial motion. To derive d²r/dt² for purely radial motion we can divide through equation (1) of Section 6.4 by (dt)² to give

Solving for dr/dt gives

where τ is the proper time of the radially moving particle. (The sign corresponds to a rising or falling trajectory.) Also, we can substitute the expressions for dr/dτ from equations (7a) and (7b) of Section 6.4 into the metric line element to give

where k is a constant parameter of the given trajectory. Substituting into (2), we have

and therefore (with either sign) the second derivative of r with respect to t is

For a bounded trajectory we put k = 1/(1 − 2m/R) so that dr/dt = 0 at r = R. In this case k is greater than 1, and inserting this into (4) gives

At the apogee of the trajectory, when r = R, this reduces to

as expected. If R is infinite, the coordinate acceleration reduces to

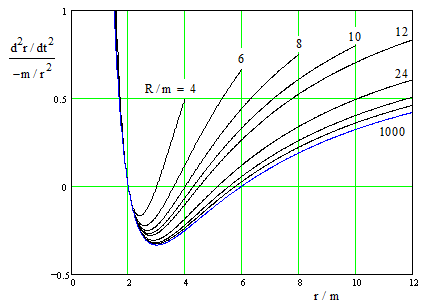
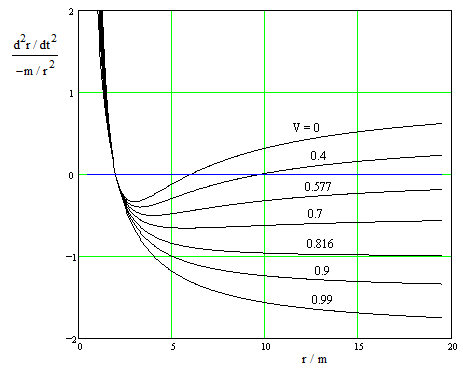
A plot of d²r/dt² divided by -m/r² for various values of R/m is shown below.

Notice that the value of (d²r/dt²) / (−m/r²) is negative in the range from r = 2m to r = 6m/(1 + 4m/R), where d²r/dt² changes from negative to positive. This signifies that the acceleration (in terms of the Schwarzschild r and t coordinates) is actually outward in this range.

For an unbounded trajectory there is no radius at which the trajectory is stationary, so the trajectory escapes to infinity, and the speed dr/dt asymptotically approaches a fixed value V in the limit as r goes to infinity. In this case we have k = (1 – V²), which is less than 1, and substituting into equation (4) gives

The case V = 0 corresponds to the case of R approaching infinity for the bound trajectories, and indeed we see that inserting V = 0 into this expression gives the same result as with R going to infinity in the acceleration equation for bound trajectories. At the other extreme, with V = 1, this equation reduces to

which is consistent with what we get for null (light-like) paths by setting dτ = 0 in the radial metric and the solving for dr/dt = ±(1 – 2m/r). A normalized plot of this acceleration for various values of V is shown below.

The acceleration d²r/dt² in terms of the Schwarzschild coordinates r and t for a particle moving radially with ultimate speed V (either toward or away from the gravitating mass) is outward at all radii greater than 2m for all ultimate speeds greater than 1/√3 (i.e., 0.577) times the speed of light. For light-like paths (V = 1), the magnitude of the acceleration approaches twice the magnitude of the Newtonian acceleration – and is outward instead of inward. The reason for this outward acceleration with respect to Schwarzschild coordinates is that the speed of light (in terms of these coordinates) is greater at greater radial distances from the mass.

Notice that the two expressions for d²r/dt² derived above, applicable to the cases when the kinetic energy of the test particle is or is not sufficient to escape to infinity, are the same if we stipulate that R and V are related according to

If R is greater than 2m, then V² is negative so V is imaginary. Hence in this case we find it most convenient to use R. On the other hand, if R is negative, from 0 to negative infinity, the value of V² is real in the range from 0 to 1, so in this case it is convenient to work with V. The remaining possibility (which has no counterpart in Newtonian gravity) is if R is between 0 and 2m, in which case V² is not only positive, it is greater than 1. Thus the impossibility of having a speed greater than 1 corresponds to the impossibility of being stationary at a radius less than 2m.

Incidentally, for a bound particle we can give an alternative derivation of the r,t acceleration from the well-known cycloidal parametric relations between r and τ (derived in Section 6.4):

where R is the "top" of the orbit and θ is an angular parameter that ranges from 0 at the top of the orbit (r = R) to p at the bottom (r = 0). Now, differentiating these parametric equations with respect to θ gives

Therefore we have

If we now define the parameter u = cos(θ) = 2r/R – 1, we have

Solving this for tan(θ/2) gives

We want θ = 0 at r = R so we choose the first root and substitute into the preceding equation for dr/dτ to give

Also, as noted above, we have the derivative of proper time with respect to coordinate time of the particle

Multiplying dr/dτ by dτ/dt  gives

Just as we did previously, we can now compute d²r/dt² = [d(dr/dt)/dr][dr/dt], and we arrive at the same result as before.

We emphasize that these expressions for acceleration are in terms of the standard Schwarzschild coordinates, and we get different expressions in terms of other systems of coordinates, such as isotropic coordinates. This highlights the importance of always understanding the operational meaning of whatever system of coordinates we are using, to establish the physical meaning of the expressions.

Return to Table of Contents