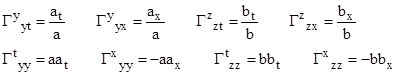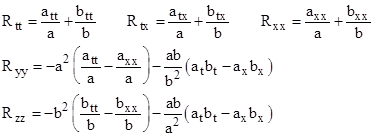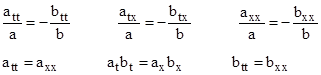6.8  Moving Sources and Gravitational Waves

This means that the velocity of propagation [of gravity] is equal to that of light. It seems at first that this hypothesis ought to be rejected outright. Laplace showed in effect that the propagation is either instantaneous or much faster than that of light. However, Laplace examined the hypothesis of finite propagation velocity ceteris non mutatis; here, on the contrary, this hypothesis is conjoined with many others, and it may be that between them a more or less perfect compensation takes place. The application of the Lorentz transformation has already provided us with numerous examples of this.

                                                                                                                Poincare, 1905

The preceding sections focused on the spherically symmetrical solution of Einstein's field equations represented by the Schwarzschild solution, combined with the geodesic hypothesis. Most of the directly observable effects of general relativity can be modeled and evaluated on this basis, i.e., in terms of the solution of the “one-body problem”, a single gravitating body that can be regarded as stationary. Having solved the field equations for this single body, we then determine the paths of test particles in its vicinity, based on the assumption that those particles do not significantly affect the field, and that they follow geodesics in the field of the gravitating body. This is obviously a very simplified and idealized case, but it happens to be fairly representative of a small planet (e.g., Mercury) orbiting the Sun, or a light pulse grazing the Sun. From one point of view, the geodesic assumption seems quite natural and unobjectionable. After all, it merely asserts Newton’s first law of motion in each small region of spacetime. Any sufficiently small region is essentially flat, and if we assume that free objects move at constant speed in straight lines in flat spacetime, then overall they follow geodesics.

However, there are two reasons for possibly being dissatisfied with the geodesic assumption. First, just as with Newton’s law of inertia, the geodesic assumption can be regarded as giving a special privileged status to certain paths without a clear justification. Of course, in practice the principle of inertia has proven itself to be extremely robust, but in theory there has always been some epistemological uneasiness about the circularity in the definition of inertial paths. As Einstein commented, we say an object moves inertially if it is free of outside influences, but we infer that it is free of outside influences only by observing that it moves inertially. This concern can be answered, at least in part, by noting that inertia serves as an organizing principle, and its significance is due to the large number of disparate entities that can be coordinated simultaneously on the basis of this principle. The concept of (local) inertial coordinates would indeed be purely circular if it successfully reduced the motions of only a single body to a simple set of patterns (e.g., Newton’s laws), but when the same system of coordinates is found to reduce the motions of multiple (and seemingly independent) objects, we are justified in claiming that it has non-trivial physical significance. Nevertheless, one of Einstein’s objectives in developing the general theory was to eliminate the reliance on the principle of inertia, which is the principle of geodesic motion in curved spacetime.

The second reason for dissatisfaction with the geodesic assumption is that all actual objects are not just passive inhabitants of the spacetime manifold, they are sources of gravitation in their own right (since all forms of mass and energy gravitate). This immediately raises the problem – also encountered in electrodynamics – of how to deal with the field produced by the moving entity itself. However, unlike Maxwell’s equations of the electrodynamic field, the field equations of general relativity are non-linear, so we are not even justified in “subtracting out” the self-field of the moving object, because the result will not generally be a solution of the field equations. One possible way of addressing this problem would be to treat the moving objects as contributors to the stress-energy tensor T_μν in the field equations, in which case the vanishing of the covariant derivative (imposed by the field equations) implies that the objects follow geodesics. However, it isn’t clear, a priori, that this is a legitimate representation of matter. Einstein, for one, rejected this approach, saying that T_μν is merely “a formal condensation of all things whose comprehension in the sense of a field theory is still problematic”. Another approach is to treat particles of matter as isolated point-like pole singularities in the field – indeed this was the basis for a paper written by Einstein, Infeld, and Hoffman (EIH) in 1938, in which they argued that (at least when the field equations are integrated to some finite order of approximation, and assuming a weak field and low accelerations) such singularities can exist only if they propagate along geodesics in spacetime.

At first sight this is a somewhat puzzling proposition, because geodesics are defined only on smooth manifolds, so it isn’t obvious how a singularity of a manifold can be said to propagate along a geodesic of that manifold. However, against the background of nearly Minkowskian spacetime, it’s possible to define a workable notion of the “position” of an isolated singularity (though not without some ambiguity). Even if we accept all these caveats, it’s odd that Einstein would pursue this approach, considering that he usually expressed a disdain for singularities, declaring that they render a field theory invalid – much like an inconsistency in a formal system. In fact, one of his favorite ideas was that we might achieve a complete physically viable field theory precisely by requiring the absence of singularities. In fact, the EIH paper itself can be seen as an example of such reasoning in the following sense.

Einstein, et al, discovered that when the field equations are integrated in the presence of two specified point-like singularities in the field propagating along timelike worldlines, a one-dimensional spacelike locus of singularity extending from one of the original points to the other generally appears in the solution. There is, however, a special set of conditions on the worldlines of the two original point-like singularities such that no intervening singular locus appears, and it is precisely the conditions of geodesic motion. Thus EIH concluded that the field equations of general relativity, by themselves, without any separate “geodesic assumption” actually do require mass point singularities to follow geodesic paths. Einstein interpreted this result to mean that even the classical equations of motion are due entirely to the non-linearity of the field equations. This is actually an example of how meaningful physics can come out of Einstein’s principle of “no-singularities”. Of course, the solution retains the two point-like singularities, so one might question whether Einstein was being hypocritical in banning singularities in the rest of the manifold. In reply he wrote

This objection would be justified if the equations of gravitation were to be considered as equations of the total field. But since this is not the case, one will have to say that the field of a material particle will differ the more from a pure gravitational field the closer one comes to the location of the particle. If one had the field equations of the total field, one would be compelled to demand that the particles themselves could be represented as solutions of the complete field equations that are free of irregularities everywhere. Only then would the general theory of relativity be a complete theory.

This is closely related to Einstein’s dissatisfaction with the dualistic nature of physics, combining the partial differential equations of the field with the total differential equations of particles. His hope was that particle-like solutions would emerge from some suitable field theory, and one of the conditions he felt must be satisfied by any such theory is the complete absence of singularities. It’s easy to understand why Einstein felt the need for a “unified field theory” to encompass both gravity and electromagnetism, because in their present separate forms they are quite incongruous. In the case of electrodynamics, the field equations are linear, and possess only a single gauge freedom, so the equations of motion must be introduced as an independent assumption. In contrast, general relativity suggests that the equations of motion of a field theory ought to be implied by the field equations themselves, which must therefore be non-linear.

One of the limitations of Einstein’s work on the equations of motion was that it neglected the effect of radiation. This neglect is usually considered to be justified, provided the accelerations involved are not too great. Still, strictly speaking, accelerating masses ought to produce radiation. Indeed, this is necessary, even for slowly accelerated motions, in order to maintain strict momentum conservation along with the nearly complete absence of aberration in the apparent direction of the “force” of gravity in the two-body problem (as noted by Laplace). But radiation reaction also causes acceleration, so it can be argued that any meaningful treatment of the problem of motion cannot neglect the effects of gravitational waves. As one would expect from a relativistic theory, the full field equations of general relativity possess solutions in which metrical disturbances propagate as waves.  For a simple example, consider a metric of the form

By the same procedure that we used in section 6.1 to derive the Schwarzschild metric, we find that the only non-zero Christoffel symbols for this metric are

where subscripts on a and b denote partial derivatives. From these we find that the only non-vanishing components of the Ricci tensor are

Setting these Ricci components to zero (for a vacuum solution of Einstein’s field equations), the quantities in parentheses must individually vanish, and we get the following conditions on the functions a(t,x) and b(t,x).

If a and b are both purely functions of u = kt – x for some constant k, then these six conditions are satisfied if and only if k² = 1 (so the phase velocity is unity, i.e., the speed of light) and

where dots signify derivatives with respect to u. We can choose any function we like for a(u), and then solve this differential equation for the corresponding function b(u) to give a solution of the vacuum field equations. For example, if we set a(u) = cos(λu) for some constant λ, then a solution is given by setting b(u) = cosh(λu). Thus we have the following well-known “wavelike” solution of the vacuum field equations

It isn’t difficult to splice a region of this solution between two regions in which the metric coefficients are purely linear functions of u, so that we have a complete vacuum spacetime that is entirely flat on both sides of a propagating plane wave. This admittedly is not a wave that could be produced by any realistic physical process, but it at least illustrates the possibility of exact wavelike solutions of the full non-linear field equations. It also shows that such waves would be expected to propagate at the speed of light. In addition, the absence of off-diagonal terms in the metric implies that the wave has two planes of polarization. One might wonder if this metric is actually physically distinct from flat Minkowski spacetime, but it can be shown that the wave carries energy (in the sense of the energy pseudo-tensor defined on a suitable background).

Many analytical treatments of gravitational waves focus on a linearized model of general relativity, but this is open to the criticism that we can’t be sure linear solutions are representative of exact solutions. (This is especially true in view of the fact that Einstein’s work on the equations of motion suggested that even the lowest order constraints on the paths are due to the non-linearity of the field equations.) Despite this, numerical simulations can now solve the full non-linear field equations with high fidelity for a wide variety of realistic scenarios.

The first empirical evidence (albeit indirect) of gravitational waves was the observed energy loss of certain binary star systems, most notably the Hulse-Taylor system, which consists of a neutron star and a pulsar orbiting each other every 8 hours. Careful observations indicate that the two stars are spiraling toward each other at a rate of 2.7 parts per billion each year, precisely consistent with the prediction of general relativity for the rate at which the system should be radiating energy in the form of gravitational waves. The agreement is very impressive, and subsequent observations of other binary star systems have provided similar indirect support for the existence of gravitational waves, although in some cases it is necessary to postulate other (unseen) bodies in the system in order to yield results consistent with general relativity.

More recently, the LIGO project (Laser Interferometer Gravitational-Wave Observatory) has reported the first direct detection of gravitational waves. Two separate facilities were built in the states of Louisiana and Washington, and their readings are combined to achieve a very large baseline. The facility in Washington state is over a mile long. The first reported detection event matches very closely the predicted signature of two fairly large black holes, of 29 and 36 solar masses, spiraling in to each other and coalescing to form a single black hole of 62 solar masses, giving off an enormous amount of energy (equivalent to 3 solar masses) as gravitational waves in the process. The source is believed to have been about 1.3 billion light years from Earth. If confirmed, this remarkable achievement could open up a new "channel" for observing the universe. In addition, it appears to provide vivid evidence of actual black holes, in close agreement with the predictions of the classical field equations of general relativity, dispelling any lingering suspicions that some unknown effect of quantum gravity might upset the classical solutions in this regime.

As discussed in Section 3.8, Einstein became convinced for a time in 1937 that gravitational waves are impossible (even in the classical context), but soon changed his mind again. As recently as 1980 there were disputes in scholarly publications as to the validity of the quadrupole solution. Part of the reason that people such as Einstein have occasionally doubted the reality of the wave solutions is that all realistic gravitational wave solutions imply a singularity (as do black holes, whose existence has also been doubted for the same reason). Also, as noted above, the inherent non-linearity of gravitational waves makes them difficult to treat analytically, and the simple linearized models are not always representative of realistic solutions. For example, it is known that there are no uniform plane wave solutions to the non-linear field equations. (The exact solution described above relies on one of the metric coefficients being cosh(t–x), which goes to infinity in both directions from the center of the wave.) There are exact cylindrical solutions, but unfortunately no plausible sources for infinite cylindrical solutions are known, so the physical significance of these solutions is unclear. Since exact analytical solutions are generally not feasible, it’s necessary to rely on numerical simulations. Fortunately these have become increasing accurate and robust with the advent of modern computers.

It might seem as though there ought to be spherically symmetrical "pulsating" solutions that radiate gravitational waves, but this is not the case, as is clear from Birkhoff's proof that the Schwarzschild solution is the unique (up to transformation of coordinates) spherically symmetrical solution of the field equations, even without the "static" assumption. In fact, we can’t even have a single oscillating mass source, because, unlike the case of electromagnetism, any entity capable of causing a mass to oscillate must also have equal and opposite mass-energy. As a result, there is no physically meaningful point source for gravitational waves in general relativity. The lowest-order solutions are necessarily given by quadrupole radiation, which may be produced by (in the simplest case) two masses oscillating back and forth connected by a spring, or by two orbiting masses.

Consideration of gravitational waves is obviously important in efforts to “quantize” the theory of gravity. Just as Planck’s analysis of electromagnetic “black body” radiation led to the quantization of the electromagnetic field (to avoid the ultra-violet catastrophe), we can consider the spectrum of gravitational waves in equilibrium within an enclosed cavity. Naturally this requires us to evaluate the state of equilibrium between the gravitational waves and the walls of the cavity, and also how the gravitational waves interact with each other. Unlike electromagnetic waves, gravitational wave solutions cannot simply be superimposed, so this is an extremely difficult situation to model. Much effort has been put into trying to understand how general relativity could be reconciled with quantum theory, but no satisfactory synthesis has emerged.

Closely related to the subject of gravitational waves is the question of how the force of gravity "propagates". It's not too surprising that the considerations of gravity in the 17th century led to the notion of instantaneous action at a distance, because it’s an empirical fact that the gravitational acceleration of a small body orbiting at a certain distance from a gravitating source is directed, at each instant, very precisely toward the position of the source at that instant. (When we refer to "instants" in this section, we mean with respect to the asymptotic inertial rest coordinates of the center of mass of the system.) Laplace noted that the stability of planetary orbits implies the absence of any appreciable aberration in the direction of the force of gravity, which led him to infer that the force of gravity must be conveyed millions of times faster than light on the assumption that gravity is a purely central force between pairs of material entities. The same reasoning would apply to the electric force between two charges, because the force of electromagnetism also exhibits no first-order aberration. However, by around 1905 Lorentz and Poincare showed that in any relativistic field theory the forces between charges or masses are not generally central, because the field itself is a dynamical element, with energy and momentum, just as are the charges or masses. The force exerted by the field on a particle at any given location and time depends not only on the past position of the source particle but also on its state of motion, due to the dynamic flows of energy and momentum that are induced in the field. This can be seen most clearly in Lorentz’s 1904 axiomatic explanation of the null result of the Trouton-Noble experiment, and Laue’s later clarification in terms of the flows of energy and momentum of the field itself. The absence of first-order aberration in the direction of the force is seen to be a direct consequence of the local conservation of total energy and momentum at every point, including particles and fields. (Alternative interpretations have been proposed that regard fields as just convenient bookkeeping conventions to represent all the central advanced and retarded interactions-at-a-distance between particles, but in such interpretations there are no isolated systems, and we must consider the mutual effects of all particles.)

This lack of aberration is obviously a necessary feature of any relativistic theory, as can be seen from examining simple interactions from different frames of reference. For example, we know the electrostatic force exerted on a uniformly moving test particle by a "stationary" charge always points directly toward the source, because the field is spherically symmetrical about the source. But we can just as well regard the test particle as "stationary", in which case the source is moving uniformly. If the force points toward the retarded position in this circumstance (i.e., with a moving source), this would signify that the laws governing electromagnetic force are different, depending on whether the source or the test particle is considered to be at rest. Empirically we find that the force exerted on the test particle always points directly toward the source at the present instant (in terms of any system of inertial coordinates). With a stationary source this is as we intuitively expect, but it may seem surprising for a moving source, because we know changes in the field propagate at the speed of light, rather than instantaneously. How does the test particle "know" where the source is at the present instant, if it can only be influenced by the source at some finite time in the past, allowing for the finite speed of propagation of the field? The answer is that the electromagnetic force function depends not only on the source's relative position, but also on the derivative of the position (i.e., the velocity). The condition of Lorentz invariance of the force law is precisely the condition that the velocity effect cancels out the lag in position, but this applies only as long as the source and the test particle continue to move uniformly. If either of them is accelerated, the "knowledge" of this propagates from one to the other at the speed of light.

An even more impressive example of the position-lag cancellation effects involves the "force of gravity" on a massive test particle orbiting a much more massive source of gravity, such as the Earth orbiting the Sun. In the case of Einstein's gravitational field equations the field interaction depends not only on the position and velocity but also on the acceleration, so the aberration cancels out not only to the first-order (as in electromagnetism) but also to the second-order. Thus the "force of gravity" on an orbiting body points almost exactly in the direction of the gravitating source at the present instant, even though the source (e.g., the Sun) is actually undergoing non-uniform motion. In the two-body problem, both objects actually orbit around the common center of mass, so the Sun (for example) actually proceeds in a circle, but the "force of gravity" exerted on the Earth effectively anticipates this motion (to the second order).

The reason the phase cancellation extends one order higher for gravity than for electromagnetism is the same reason that Maxwell's equations predict dipole waves, whereas Einstein's equations only support quadrupole (or higher) waves. Waves will necessarily appear in the same order at which phase cancellation no longer applies. For electrically charged particles we can generate waves by any kind of acceleration, because electromagnetism exists within the spacetime metric provided by the field equations, and we can accelerate a charged object by interaction with neutral objects. In contrast, we can't produce gravitational waves by the simplest kind of "acceleration" of a mass, because there is no background reference to unambiguously define dipole acceleration, and any manipulation of a mass must be performed by some other mass. The Einstein field equations have an extra degree of freedom (so to speak) that prevents simple dipole acceleration from having any "traction". It is necessary to apply quadrupole acceleration, so that the two dipoles can act on each other to yield a propagating effect.

A two-body system such as the Sun and the Earth produces very little gravitational radiation, and accordingly has nearly perfect compensation for the position-lag, so the Earth's gravitational acceleration always points directly toward the Sun's position at the present instant, rather than (say) the Sun's position eight minutes ago. Nevertheless, if the Sun were to suddenly split into two parts that recoiled from each other, the effect of such a disturbance in the Sun’s gravitational field would propagate at the speed of light. Thus the fact that the Earth's gravitational acceleration always points directly at the Sun's present position does not imply that the "force of gravity" is transmitted instantaneously. It merely implies that there are velocity and acceleration terms in the interaction (corresponding to the dynamics of the gravitational field) that effectively cancel out the position lag in a simple periodic pattern of motion.

In 1917 James Jeans noted that if electromagnetism propagates at the speed of light but gravity propagates instantaneously then the shape of celestial bodies would not be Lorentz invariant, because "a compromise would be effected between electromagnetic forces, striving for a Fitzgerald ellipsoid, and the gravitational forces striving for a strictly spherical shape”, and this would enable us to determine the absolute speed of the body. The absence of any such “compromises” (in the ocean tides for example) can be taken as evidence that the (weak) gravitational force does indeed propagate at the speed of light.

One might wonder how momentum can be strictly conserved in the presence of “non-central forces”. The answer is that the term “non-central” is somewhat misleading, because it refers to the direction between two charges or masses, which we often regard (somewhat inaccurately) as the only carriers of momentum. To correctly account for the total flow of momentum, we must also consider the momentum currents associated with the flow of energy in the fields. Of course, at the higher orders where there actually is some slight aberration, the compensating flow of momentum is in the form of radiation in the field. But at the lower orders, where aberration is cancelled out by the apparent “non-centrality” of the interaction, the compensating flow of momentum is in the non-radiative flow of energy and momentum in the field. The importance of energy-momentum flows in the fields as viewed from different frames of reference was first highlighted by von Laue in his 1911 explanation of the absence of torque in the Trouten-Noble experiment. Lorentz and Poincare had already noted that no torque was to be expected from simple consideration of the relativity principle which implies that all forces transform in the same way under a Lorentz transformation, resulting in “non-central forces”. But von Laue explained clearly how this was consistent with conservation of momentum when we take into account the momentum currents of the energy flowing through the field. Recall that, for electromagnetism, Poynting’s vector S = E x B represents the flow of energy, and not just in a radiative sense, but any time E and B are non-zero, which is the case whenever (for example) two charges are moving uniformly relative to each other. Analogous flows of energy and momentum can be identified in the gravitational field, accounting for the low-order absence of aberration.

Return to Table of Contents