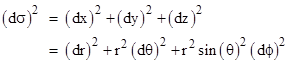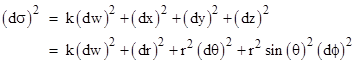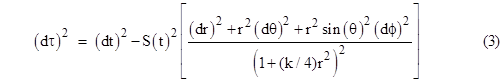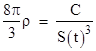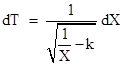|
7.1 Is the Universe Closed? |
|
The unboundedness of space has a greater empirical certainty than any experience of the external world, but its infinitude does not in any way follow from this; quite the contrary. Space would necessarily be finite if one assumed independence of bodies from position, and thus ascribed to it a constant curvature, as long as this curvature had ever so small a positive value. |
|
B. Riemann, 1854 |
|
Very soon after arriving at the final form of the field equations, Einstein began to consider their implications with regard to the overall structure of the universe. His 1917 paper presented a simple model of a closed spherical universe which "from the standpoint of the general theory of relativity lies nearest at hand". In order to arrive at a quasi-static distribution of matter he found it necessary to introduce the "cosmological term" to the field equations (as discussed in Section 5.8), so he based his analysis on the equations |
|
|
|
|
|
where l is the cosmological constant. (We choose units so that the speed of light and Newton’s gravitational constant are both equal to 1.) Before invoking the field equations we can consider the general form of a metric that is suitable for representing the large-scale structure of the universe. First, we ordinarily assume that the universe would appear to be more or less the same when viewed from the rest frame of any galaxy, anywhere in the universe (at the present epoch). This is sometimes called the Cosmological Principle. |
|
|
|
Then, since the universe on a large scale appears (to us) highly homogenous and isotropic, we infer that these symmetries apply to every region of space. This greatly restricts the class of possible metrics. In addition, we can choose, for each region of space, to make the time coordinate coincide with the proper time of the typical galaxy in that region. Also, according to the Cosmological Principle, the coefficients of the spatial terms of the (diagonalized) metric should be independent of location, and any dependence on the time coordinate must apply symmetrically to all the space coordinates. From this we can infer a metric of the form |
|
|
|
|
|
|
|
where s(t) is some (still to be determined) dimensionless scale factor dependent on time, and dσ is the total space differential with no time dependence. In other words, the “shape” of the spatial metric is fixed, but the scale factor is a function of time. Recall that for a perfectly flat Euclidean space the differential line element is |
|
|
|
|
|
|
|
where r2 = x2 + y2 + z2. On the other hand, if we want to allow our space (at a given coordinate time t) to have curvature, the Cosmological Principle suggests that the (large scale) curvature should be the same everywhere and in every direction. Thus the Gaussian curvature of every two-dimensional tangent subspace has the same value at every point. Now suppose we embed a Euclidean three-dimensional space (x,y,z) in a four-dimensional space (w,x,y,z) whose metric is |
|
|
|
|
|
|
|
where k is either +1 or −1. If k = +1 the four-dimensional space is Euclidean, whereas if k = −1 it is pseudo-Euclidean (like the Minkowski metric). In either case the four-dimensional space is "flat", i.e., has zero Riemannian curvature. We then consider a three-dimensional subspace comprising a sphere (or pseudo-sphere), i.e., the locus of points satisfying the condition |
|
|
|
|
|
|
|
where A is a constant characteristic length. From this we have w2 = A2 – kr2, and therefore |
|
|
|
|
|
|
|
Substituting this into the four-dimensional line element above gives the metric for the three-dimensional sphere (or pseudo-sphere) |
|
|
|
|
|
|
|
Taking this as the spatial part of our overall spacetime metric (2), replacing r with Ar (so r is now dimensionless), and defining S(t) = As(t), we arrive at |
|
|
|
|
|
|
|
This metric, with k = +1 and S(t) = constant, was the basis of Einstein's 1917 paper, and it was subsequently studied by Alexander Friedmann in 1922 with both possible signs of k and with variable S(t). The general form was re-discovered by Robertson and Walker (independently) in 1935, so it is now often referred to as the Robertson-Walker metric. Notice that with k = +1 this metric essentially corresponds to polar coordinates on the "surface" of a sphere projected onto the "equatorial plane", so each value of r corresponds to two points, one in the Northern and one in the Southern hemisphere. We could remedy this by making the change of variable r → r/(1 + kr2/4), which (in the case k = +1) amounts to stereographic projection from the North pole to a tangent plane at the South pole. In terms of this transformed radial variable the Robertson-Walker metric has the form |
|
|
|
|
|
|
|
As noted above, Einstein originally assumed S(t) = constant, i.e., he envisioned a static un-changing universe. He also assumed the matter in the universe was roughly "stationary" at each point with respect to these cosmological coordinates, so the only non-zero component of the stress-energy tensor in these coordinates is Ttt = ρ where ρ is the density of matter (assumed to be uniform, in accord with the Cosmological Principle). On this basis, the field equations imply |
|
|
|
|
|
|
|
Here the symbol S denotes the assumed constant value of S(t). This explains why Einstein was originally led to introduce a non-zero cosmological constant λ, because if we assume a static universe and the Cosmological Principle, the field equations of general relativity can only be satisfied if the density ρ is proportional to the cosmological constant. However, it was soon pointed out that this static model is unstable, so it is a priori unlikely to correspond to the physical universe. Moreover, astronomical observations subsequently indicated that the universe (on the largest observable scale) is actually expanding, so we shouldn't restrict ourselves to models with S(t) = constant. If we allow S(t) to be variable, then the original field equations, without the cosmological term (i.e., with λ = 0), do have solutions. In view of this, Einstein decided the cosmological term was unnecessary and should be excluded. |
|
|
|
Interestingly, George Gamow was working with Friedmann in Russia in the early 1920's, and later recalled that "Friedmann noticed that Einstein had made a mistake in his alleged proof that the universe must necessarily be stable". Specifically, Einstein had divided through an equation by a certain quantity, even though that quantity was zero under a certain set of conditions. As Gamow notes, "it is well known to students of high school algebra" that division by zero is not valid. Friedmann realized that this error invalidated Einstein's argument against the possibility of a dynamic universe, and indeed under the condition that the quantity in question vanishes, it is possible to satisfy the field equations with a dynamic model, i.e., with a model of the form given by the Robertson-Walker metric with S(t) variable. It's worth noting that Einstein's 1917 paper did not actually contain any alleged proof that the universe must be static, but it did suggest that a non-zero cosmological constant required a non-zero density of matter. Shortly after Einstein's paper appeared, de Sitter gave a counter-example (see Section 7.6), i.e., he described a model universe that had a non-zero λ but zero matter density. However, unlike Einstein's model, it was not static. Einstein objected strenuously to de Sitter's model, because it showed that the field equations allowed inertia to exist in an empty universe, which Einstein viewed as "inertia relative to space", and he still harbored hopes that general relativity would fulfill Mach's idea that inertia should only be possible in relation to other masses. It was during the course of this debate that (presumably) Einstein advanced his "alleged proof" of the impossibility of dynamic models (with the errant division by zero?). However, before long Einstein withdrew his objection, realizing that his argument was flawed. Years later he recalled the sequence of events in a discussion with Gamow, and made the famous remark that it had been the biggest blunder of his life. This is usually interpreted to mean that he regretted ever considering a cosmological term (which seems to have been the case), but it could also be referring to his erroneous argument against the idea of a dynamic universe, resulting from his unfortunate "division by zero". |
|
|
|
In any case, the Friedmann universes (with and without cosmological constant) became the "standard model" for cosmologies. If k = +1 the manifold represented by the Robertson-Walker metric is a finite spherical space, so it is called "closed". If k = 0 or –1 the metric is typically interpreted as representing an infinite space, so it is called "open". However, it's worth noting that this need not be the case, because the metric gives only local attributes of the manifold; it does not tell us the overall global topology. For example, we discuss in Section 7.4 a manifold that is everywhere locally flat, but that is closed cylindrically. This shows that when we identify "open" (infinite) and "closed" (finite) universes with the cases k = −1 and k = +1 respectively, we are actually assuming the "maximal topology" for the given metric in each case. |
|
|
|
Based on the Robertson-Walker metric (3), we can compute the components of the Ricci tensor and scalar and substitute these along with the simple uniform stress-energy tensor into the field equations (1) to give the conditions on the scale function S = S(t): |
|
|
|
|
|
|
|
|
|
where dots signify derivatives with respect to t. As expected, if S(t) is constant, these equations reduce to the ones that appeared in Einstein's original 1917 paper, whereas with variable S(t) we have a much wider range of possible solutions. |
|
|
|
It may not be obvious that these two equations have a simultaneous solution, but notice that if we multiply the first condition through by S(t)3 and differentiate with respect to t, we get |
|
|
|
|
|
|
|
The left-hand side is equal
to |
|
|
|
|
|
|
|
With this stipulation, the two conditions are redundant, i.e., a solution of one is guaranteed to be a solution of the other. Substituting for (8π/3)ρ in the first condition and multiplying through by S(t)3, we arrive at the basic differential equation for the scale parameter of a Friedmann universe |
|
|
|
|
|
|
|
Incidentally, if we
multiply through by S(t), differentiate with respect to t, divide through by |
|
|
|
|
|
|
|
With λ = 0 this is
identical to the gravitational separation equation (3) in Section 4.2,
showing that the cosmological scale parameter S(t) is yet another example of
a naturally occurring spatial separation that satisfies this differential
equation. It follows that the admissible functions S(t) (with λ = 0) are
formally identical to the gravitational free-fall solutions described in
Section 4.3. Solving equation (4) (with λ = 0) for |
|
|
|
|
|
|
|
Accordingly as k equals −1, 0, or +1, integration of this equation gives |
|
|
|
|
|
|
|
|
|
|
|
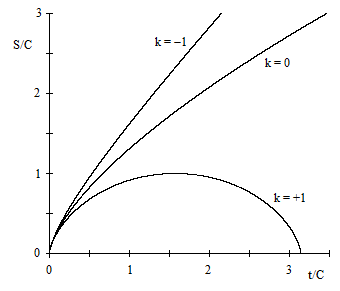
A plot of these three solutions is shown below. |
|
|
|
|
|
|
|
In all three cases with λ = 0, the expansion of the universe is slowing down, albeit only slightly for the case k = −1. However, if we allow a non-zero cosmological constant λ, there is a much greater variety of possible solutions to Friedmann's equation (2), including solutions in which the expansion of the universe is actually accelerating exponentially. Based on the cosmic scale parameter S and its derivatives, the three observable parameters traditionally used to characterize a particular solution are |
|
|
|
|
|
|
|
|
|
|
|
In terms of these parameters, the constants appearing in the Friedmann equation (4) can be expressed as |
|
|
|
|
|
|
|
In principle if astronomers could determine the values of H, q, and σ with enough precision, we could decide on empirical grounds the sign of k, and whether or not λ is zero. Thus, assuming the maximal topologies (and the large-scale validity of general relativity), we could determine whether the universe is open or closed, and whether it will expand forever or eventually re-contract. Unfortunately, none of the parameters is known with enough precision to distinguish between these possibilities. |
|
|
|
One source of uncertainty is in the estimates of the mass density ρ of the universe. Given the best current models of star masses, and the best optical counts of stars in galaxies, and the apparent density of galaxies, we estimate an overall mass density that is only a small fraction of what would be required to make k = 0. However, there are reasons to believe that much (perhaps most) of the matter in the universe is not luminous. (For example, the observed rotation of individual galaxies indicates that they ought to fly apart unless there is substantially more mass in them than is visible to us.) This has led physicists and astronomers to search for the "missing mass" in various forms. |
|
|
|
Another source of uncertainty is in the values of S and its derivatives. For example, in its relatively brief history, Hubble's constant has undergone revisions of an order of magnitude, both upwards and downwards. In recent years the Hubble space telescope and several modern observatories on Earth seem to have found strong evidence that the expansion of the universe is actually accelerating. If so, then it could be accounted for in the context of general relativity only by a non-zero cosmological constant λ (on a related question, see Section 7.6), with the implication that the universe is infinite and will expand forever (at an accelerating rate). |
|
|
|
Nevertheless, the idea of a closed finite universe is still of interest, partly because of the historical role it played in Einstein's thought, but also because it remains (arguably) the model most compatible with the spirit of general relativity. In an address to the Berlin Academy of Sciences in 1921, Einstein said |
|
|
|
I must not fail to mention that a theoretical argument can be adduced in favor of the hypothesis of a finite universe. The general theory of relativity teaches that the inertia of a given body is greater as there are more ponderable masses in proximity to it; thus it seems very natural to reduce the total effect of inertia of a body to action and reaction between it and the other bodies in the universe... From the general theory of relativity it can be deduced that this total reduction of inertia to reciprocal action between masses - as required by E. Mach, for example - is possible only if the universe is spatially finite. On many physicists and astronomers this argument makes no impression... |
|
|
|
This is consistent with the approach taken in Einstein's 1917 paper. Shortly thereafter he presented (in "The Meaning of Relativity", 1922) the following three arguments against the conception of infinite space, and for the conception of a bounded, or closed, universe: |
|
|
|
(1) From the standpoint of the theory of relativity, to postulate a closed universe is very much simpler than to postulate the corresponding boundary condition at infinity of the quasi-Euclidean structure of the universe. |
|
|
|
(2) The idea that Mach expressed, that inertia depends on the mutual attraction of bodies, is contained, to a first approximation, in the equations of the theory of relativity; it follows from these equations that inertia depends, at least in part, upon mutual actions between masses. Thereby Mach's idea gains in probability, as it is an unsatisfactory assumption to make that inertia depends in part upon mutual actions, and in part upon an independent property of space. But this idea of Mach's corresponds only to a finite universe, bounded in space, and not to a quasi-Euclidean, infinite universe. From the standpoint of epistemology it is more satisfying to have the mechanical properties of space completely determined by matter, and this is the case only in a closed universe. |
|
|
|
(3) An infinite universe is possible only if the mean density of matter in the universe vanishes. Although such an assumption is logically possible, it is less probable than the assumption of a finite mean density of matter in the universe. |
|
|
|
Misner, Thorne, and Wheeler ("Gravitation") were evidently sympathetic to Einstein’s view, and even claim that general relativity "demands closure of the geometry in space as a boundary condition on the initial-value equations if they are to yield a well-determined and unique 4-geometry." Interestingly, when they quote Einstein's reasons in favor of a closed universe they omit the third without comment, although it reappears (with a caveat) in the subsequent "Inertia and Gravitation" of Ciufolini and Wheeler. As we've seen, Einstein was initially under the mistaken impression that the only cosmological solutions of the field equations are those with |
|
|
|
|
|
|
|
where S is the radius of curvature of the universe and ρ is the mean density of matter. (In our units the gravitational constant equals unity.) This much is consistent with modern treatments, which agree that at any given epoch in a Friedmann universe with constant non-negative curvature the radius is inversely proportional to the square root of the mean density. On the basis of (5) Einstein continued |
|
|
|
If the universe is quasi-Euclidean, and its radius of curvature therefore infinite, then ρ would vanish. But it is improbable that the mean density of matter in the universe is actually zero; this is our third argument against the assumption that the universe is quasi-Euclidean. |
|
|
|
However, in the 2nd edition of "The Meaning of Relativity" (1945), he added an appendix, "essentially nothing but an exposition of Friedmann's idea", i.e., the idea that "one can reconcile an everywhere finite density of matter with the original form of the equations of gravity [without the cosmological term] if one admits the time variability of the metric distances...". In this appendix he acknowledged that in a dynamic model, as described above, it is perfectly possible to have an infinite universe with positive density of matter, provided that k = −1. It's clear that Einstein originally had not seriously considered the possibility of a universe with positive mass density but overall negative curvature. In the first edition, whenever he mentioned the possibility of an infinite universe he referred to the space as "quasi-Euclidean", which I take to mean "essentially flat". He regarded this open infinite space as just a limiting case of a closed spherical universe with infinite radius. He simply did not entertain the possibility of a hyperbolic (k = −1) universe. (It's interesting that Riemann, too, excluded spaces of negative curvature from his 1854 lecture, without justification.) His basic objection was evidently that a spacetime with negative curvature possesses an inherent structure independent of the matter it contains, and he was unable to conceive of any physical source of negative curvature. This typically entails "ad hoc" boundary conditions at infinity, precisely what's required in an open universe, which Einstein regarded as contrary to the spirit of relativity. |
|
|
|
At the end of the appendix in the 2nd edition, Einstein conceded that it comes down to an empirical question. If (8π/3)ρ is greater than H2, then the universe is closed and spherical; otherwise it is open and flat or pseudospherical (hyperbolic). He also makes the interesting remark that although we might possibly prove the universe is spherical, "it is hardly imaginable that one could prove it to be pseudospherical". His reasoning is that in order to prove the universe is spherical, we need only identify enough matter so that (8π/3)ρ exceeds H2, whereas if our current estimate of ρ is less than this threshold, it will always be possible that there is still more "missing matter" that we have not yet identified. At this stage Einstein was assuming a zero cosmological constant, so it may not have occurred to him that it might someday be possible to determine empirically that the expansion of the universe is accelerating. |
|
|
|
Ironically, already in 1919 Einstein had written privately to Lorentz acknowledging the weakness of the idea that the universe must be closed. |
|
|
|
My view that the state of the ether (i.e., the gmn’s) must be determined by the matter alone has nothing compelling about it. That is why one cannot argue for the closure of the world with as much certainty as I have done. |
|
|
|
His use of the word “ether” for the gravitational/inertial field was in deference to Lorentz, but even aside from that, this is a remarkable statement, considering how strongly Einstein subsequently continued to promote the concept of a closed universe, based on the Machian idea that the metrical field “must be determined by the matter alone”. Even after he later disavowed “Mach’s principle”, he went on arguing in favor of a closed universe. |
|
|
|
Ultimately, was there any merit in Einstein's skepticism toward the idea of an "open" universe? Even setting aside his third argument, the first two still carry some weight with some people, especially those who are sympathetic to Mach's ideas regarding the relational origin of inertia. In an open universe we must accept the fact that there are multiple, physically distinct, solutions compatible with a given distribution of matter and (non-gravitational) energy. In such a universe the "background" inertial field can in no way be attributed to the matter and energy content of the universe. From this standpoint, general relativity can never give an unambiguous answer to the twins paradox (for example), because the proper time integral over a given path from A to B depends on the inertial field, and in an open universe this field cannot be inferred from the distribution of mass-energy. It is determined primarily by whatever absolute boundary conditions we choose to impose, independent of the distribution of mass-energy. Einstein believed that such boundary conditions were inherently non-relativistic, because they require us to single out a specific frame of reference − essentially Newton's absolute space. (In later years a great deal of work has been done in attempting to develop boundary conditions "at infinity" that do not single out a particular frame. This is discussed further in Section 7.7.) |
|
|
|
The only alternative (in an open universe) that Einstein could see in 1917 was for the metric to degenerate far from matter in such a way that inertia vanishes, i.e., we would require that the metric at infinity go to something like |
|
|
|
|
|
|
|
Such a boundary condition would be the same with respect to any frame of reference, so it wouldn't single out any specific frame as the absolute inertial frame of the universe. Einstein pursued this approach for a long time, but finally abandoned it because it evidently implies that the outermost shell of stars must exist in a metric very different from ours, and as a consequence we should observe their spectral signatures to be significantly shifted. (At the time there was no evidence of any "cosmological shift" in the spectra of the most distant stars. We can only speculate how Einstein would have reacted to the discovery of quasars, the most distant objects known, which are in fact characterized by extreme redshifts and apparently extraordinary energies.) |
|
|
|
The remaining option that Einstein considered for an open asymptotically flat universe is to require that, for a suitable choice of the system of reference, the metric must go to |
|
|
|
|
|
|
|
at infinity. However, the imposition of this condition in a spherically symmetrical way (for example) singles out one particular frame of reference as the absolute inertial frame of the universe with no relational foundation. This, Einstein said, "is contrary to the spirit of the relativity principle", and it was the basis of his early view that general relativity is most compatible with a closed unbounded universe. The recent astronomical findings that seem to indicate an accelerating expansion have caused most scientists to abandon closed models, but there seems to be some lack of appreciation for the damage an open universe does to the epistemological strength of general relativity. As Einstein wrote in 1945, "the introduction of [the cosmological constant] constitutes a complication of the theory, which seriously reduces its logical simplicity". |
|
|
|
Of course, in either an open or a closed universe, a theory consisting of differential equations requires boundary and/or initial conditions, but the question is whether the distribution of mass-energy by itself is adequate to define the field, or whether independent boundary conditions on the metrical field are necessary to uniquely determine the field. In a closed universe the metrical structure can be more directly attributed to (or at least associated with) the distribution of mass-energy, whereas in an open universe this is not generally possible. The seriousness of this depends on how seriously we take Mach's principle and the need to identify the origin of inertia. |
|
|
|
In a 1917 paper Einstein noted that some people, such as de Sitter, argued that we need not concern ourselves with the origin of inertia, global boundary conditions, etc., because we can simply specify the metric at the spatial limit of the finite domain under consideration, just as we empirically determine the inertial frames when working in Newtonian mechanics. Not surprisingly, Einstein was unenthusiastic about this approach, because it implies that the principles of general relativity must be augmented by arbitrary boundary conditions in order to yield determinate results. He still hoped that general relativity might fully constrain the possibilities and yield a unique structure for the universe, explaining the origin of inertia. Regarding de Sitter’s pragmatic suggestion he said |
|
|
|
…such a complete resignation in this fundamental question is for me a difficult thing. I should not make up my mind to it until every effort to make headway toward a satisfactory view had proved to be in vain. |
|
|
|
One might argue that the metric field of spacetime itself is a dynamical entity in general relativity, so Mach's view distinguishing space and time from things that exist within space and time is no longer relevant. Indeed, near the end of his life Einstein wrote (in a 1954 letter to Felix Pirani) |
|
|
|
In my view one should no longer speak of Mach's principle at all. It dates back to the time in which one thought that the 'ponderable bodies' are the only physically real entities and that all elements of the theory which are not completely determined by them should be avoided. (I am well aware of the fact that I myself was long influenced by this idee fixe.) |
|
|
|
Despite this, the metrical field of spacetime is not an observable of the theory, so proponents of Mach’s view may still claim that the conditions ought to be specifiable, and inertia ought to be explainable, purely in terms of the interactions and phase relations of the “ponderable” (non-gravitational) mass-energy. The metric field in an open infinite universe relies on some constraints beyond what can be attributed to the mass-energy interactions and phase relations, so if the universe is open and infinite – as current astronomical data suggests – the Machian is forced to conclude that general relativity is incomplete, i.e., that there must be something other than the field equations of general relativity determining which of the possible structures actually exists. Even after discounting Mach’s principle, Einstein continued to believe that the introduction of a cosmological constant seriously undermines the logical simplicity of general relativity. Indeed the cosmological constant (or dark energy) currently proposed to account for accelerating expansion, and the various inflationary models of the early universe, show how much simplicity has been lost in comparison with the original Friedmann models. |
|
|