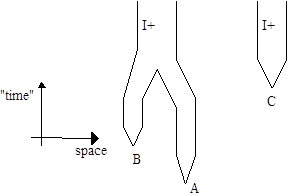7.2† The Formation and Growth of Black Holes |
|
|
|
It is a light thing for the shadow to go down ten degrees: nay, but let the shadow return backward ten degrees. |
|
2 Kings 20 |
|
|
|
One of the most common questions about black holes is how they can exist if it takes infinitely long (from the perspective of an outside observer) for anything to reach the event horizon. The usual response is to explain that although the Schwarzschild coordinates are ill-behaved at the event horizon, the intrinsic structure of spacetime itself is well-behaved in that region, and an infalling object passes through the event horizon in finite proper time of the object. This is certainly an accurate description of the Schwarzschild structure (as discussed in Section 6.4), but it may not fully address the question, which can be summarized in terms of the following two seemingly contradictory facts: |
|
|
|
(1) An event horizon can grow only if the mass contained inside the horizon increases. |
|
(2) Nothing crosses the event horizon in finite Schwarzschild coordinate time. |
|
|
|
Item (1) is a consequence of the fact that, as in Newtonian gravity, the field contributed by a (static) spherical shell on its interior is zero, so an event horizon can't be expanded by accumulating mass on its exterior. Nevertheless, if mass accumulates near the exterior of a black hole's event horizon the gravitational radius of the combined system must eventually increase far enough to encompass the accumulated mass, leading unavoidably to the conclusion that matter from the outside must reach the interior, and it must do so in a way that is perceptible in finite coordinate time for a distant observer, which seems to directly conflict with Item 2 (and certainly seems inconsistent with the "frozen star" interpretation). To resolve this apparent paradox requires a careful examination of the definition of a black hole, and of the behavior of the Schwarzschild time coordinate near an event horizon. This leads directly to several interesting results, such as the fact that if two black holes merge, then their event horizons are contiguous, and have been so since they were formed. |
|
|
|
We can consider first how the matter content of a black hole is increased when it combines with another black hole. In such a case we obviously aren't dealing with a simple "one-body problem", so the spherically symmetrical Schwarzschild solution is not applicable. Lacking an exact solution of the field equations for the two-body problem, we can at least get a qualitative idea of the process by examining the "trousers" topology shown below: |
|
|
|
|
|
|
|
As we progress through the sequence of external time slices the first event horizon appears at A, then another appears at B, then at C, and then A and B merge together. The "surfaces" of the trousers represent future null infinity (I+) of the external region, consistent with the definition of black holes as regions of spacetime that are not in the causal past of future null infinity. (If the universe is closed, the "ceiling" from which these "stalactites" descend is at some finite height, and our future boundary is really just a single surface. In such a universe these protrusions of future infinity are not true "event horizons", making it difficult to give a precise definition of a black hole. In this discussion we assume an infinite open universe.) The "interior" regions enclosed by these surfaces are, in a sense, beyond the infinite future of our region of spacetime. If we regard a small test object as a point particle with zero radius then it's actually a black hole too, and the process of "falling in" to a "macro" black hole would simply be the trousers operation of merging the two I+ surfaces together, just like the merging of two macro black holes. |
|
|
|
On this basis the same interpretation would apply to the original formation of a macro black hole, by the coalescing of the I+ surfaces represented by the individual particles of the original collapsing star. Thus, we can completely avoid the "paradox" of black hole formation by considering all particles of matter to already be black holes. According to this view, it makes no sense to talk about the "interior" of a black hole, any more than it makes sense to talk about what's "outside" the universe, because the surface of a black hole is a boundary (future null infinity) of the universe. |
|
|
|
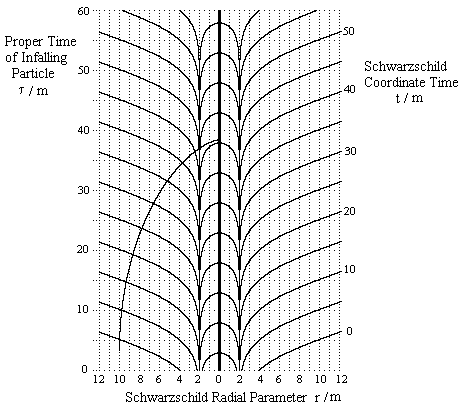
Unfortunately, it isn't at all clear that small particles of matter can be regarded as black holes surrounded by their own microscopic event horizons, so the "trousers" approach may not be directly applicable to the accumulation of small particles of "naked matter" (i.e., matter not surrounded by an event horizon). We'd like an explanation for the absorption of matter into a black hole that doesn't rely on this somewhat peculiar model of matter. To reconcile the Schwarszchild solution with the apparent paradox presented by items (1) and (2) above, it's worthwhile to recall from Chapter 6.4 what a radial freefall path really looks like in simple Schwarzschild geometry. We saw that the radial position of a test particle starting at radius r = 10m and t = 0 (for example) as a function of the particleís proper time is a simple cycloid right down to r = 0, whereas if the same trajectory is described in terms of Schwarzschild coordinate time, the infalling object traverses through infinite coordinate time in order to reach the event horizon, and then traverses back through an infinite range of coordinate times until reaching r = 0 (in the interior) in a net coordinate time that is not too different from the elapsed proper time. In other words, the object goes infinitely far into the "future" (of coordinate time), and then infinitely far back to the "present" (also in coordinate time), and since these two segments must always occur together, we can "re-normalize" the round trip and just deal with the net change in coordinate time (for any radius other than precisely r = 2m). |
|
|
|
Admittedly itís unorthodox to attribute any physical significance to the Schwarzschild time coordinate of a particle passing through the event horizon, and to some extent this is justified, because this coordinate is, after all, just a labeling of events. Moreover, as discussed in Section 6.4, the mapping of the Schwarzschild time coordinate from outside to inside the event horizon is formally arbitrary. Symmetrical drawings of the fully extended Kruskal solution, including a white hole as well as a black hole, tend to disguise this ambiguity, because they strongly suggest a symmetrical alignment of the time coordinates outside and inside the horizon, but this symmetry isnít required by the equations. This interpretation is permitted by the equations, so it may still be worth considering. Also, the Schwarzschild time coordinate is physically significant in the sense that it is the unique time coordinate in terms of which the spherically symmetrical solution is static, i.e., the metric coefficients are independent of time. In other words, the time coordinate is a Killing vector field. The existence of a singularity in a Killing vector has global significance, being a one-way causal boundary. |
|
|
|
One possible objection to the physical significance of the Schwarzschild time coordinates is the fact that a single infalling object occupies two different places (one inside and one outside the event horizon) at the same coordinate time. However, this shouldn't be surprising, because worldlines need not be single-valued in terms of arbitrary curvilinear coordinates. Still, it might seem that this "dual presence" opens the door to time-travel paradoxes. For example, we can observe the increase in the gravitational radius at some finite coordinate time, when the particle that caused the increase has still not yet crossed the event horizon (using the terms "when" and "not yet" in the sense of coordinate time), so it might seem that we have the opportunity to retrieve the particle before it crosses the horizon, thus preventing the increase that triggered our retrieval! However, if we carefully examine the path of the particle, both outside and inside the event horizon, we find that by the time it has gotten "back" close to our present coordinate time on the interior branch, the exterior branch is past the point of last communication. Even a photon could not catch up with it prior to crossing the horizon. The "backward" portion of the particle's trajectory through coordinate time inside the horizon ends just short of enabling any causality paradoxes. (It's apparent from these considerations that classical relativity must be a strictly deterministic theory - in which each worldline can be treated as already existing in its entirety - because we could construct genuine paradoxes in a non-deterministic theory.) |
|
|
|
Itís also worth noticing that the two strategies described above for explaining the formation and growth of black holes are essentially the same. In both cases the event horizon "reaches back" to us all the way from future null infinity. In a sense, that's why the infalling geodesics in Schwarzschild space go to infinity at the event horizon. To show the correspondence more clearly, we can turn the figure in Section 6.4 on end (so the coordinate time axis is vertical) and then redraw the constant-t lines as curves so as to accurately represent the absolute spacetime intervals. The result is shown below for a small infalling test particle: |
|
|
|
|
|
|
|
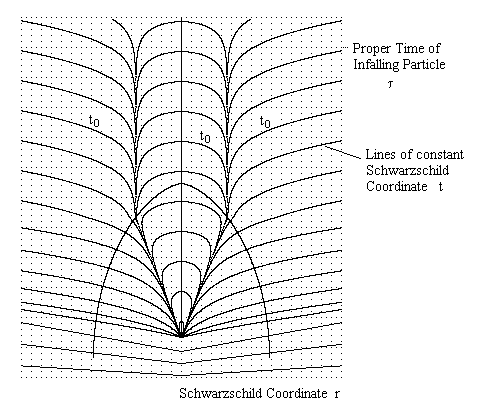
Notice that the infalling worldline passes through all the Schwarzschild time slices t as it crosses the event horizon. Now suppose we take a longer view of this, beginning all the way back at the point of formation of the black hole, and suppose the infalling mass is significant relative to the original mass m. The result looks like this: |
|
|
|
|
|
This shows how the stalactite reaches down from future infinity, and how the infalling mass passes through this infinity - but in finite proper time - to enter the interior of the black hole, and the event horizon expands accordingly. This figure is based on the actual spacetime intervals, and shows how the lines of constant Schwarzschild time t wrap around the exterior of the event horizon down to the point of formation, where they enter the interior of the black hole and "expand" back close to the region where they originated on the outside. |
|
|
|
One thing that sometimes concerns people when they look at a radial free-fall plot in Schwarzschild coordinates is related to the left hand side of the ballistic trajectory. Does the symmetry of the figure imply that we could launch a particle from r = 0, have it climb up to 5m, and then drop back down? No, because the light cones have tipped over at 2m, so the timelike and spacelike axes are reversed. Inside the event horizon the effective time axis points parallel to "r". As a result, although the left hand trajectory in the region above 2m is possible, the portion for r less than 2m is not; it's really just the time-reversed version of the right hand side. (We could also imagine a topology in which all inward and outward trajectories are realized (Kruskal space), but there is no known mechanism that would generate such a structure.) |
|
|
|
Still, it's valid to ask "how did we decide which way was forward in time inside the event horizon?" The only formal requirement seems to be that our choice be consistent for any given event horizon, always increasing r or always decreasing r. If we make one choice of sign convention we have a "white hole" spewing objects outward into our universe, whereas if we make the opposite choice we have a black hole, drawing things inward. The question of whether we should expect to find as many white holes as black holes in the universe is still a subject of lively debate. |
|
|
|
In the forgoing reference was made to mass accumulating "near" the horizon, but we need to be careful about the concepts of nearness. The intended meaning in the above context was that the mass is (1) exterior to the event horizon, and (2) within a small increment Dr of the horizon, where r is the radial Schwarzschild coordinate. I've also assumed spherical symmetry so that the Schwarzschild solution and Birkhoff's uniqueness proof apply (meaning that the spacetime in the interior of an empty spherically symmetrical shell is necessarily flat). |
|
|
|
Of course, in terms of the spacelike surfaces of simultaneity of an external particle, the event horizon is always infinitely far away, or, more accurately, the horizon doesn't intersect with any external spacelike surface, with the exception of the single degenerate time&space-like surface precisely at 2m, where the external time and space surfaces close on each other like scissors (and then swap roles in the interior). So in terms of these coordinates the particle is infinitely far from the horizon right up to the instant it crosses the horizon! And this is the same "instant" that every other infalling object crosses the horizon, although separated by great "distances". (This isn't really so strange. Midnight tonight is infinitely far from us in this same sense, because it is no finite spatial distance away, and it will remain so until the instant we reach it. Likewise the event horizon is ahead of us in time, not in space.) |
|
|
|
Incidentally, we should perhaps qualify our dismissal of the "frozen star" interpretation, because it does (arguably) give a servicable account of phenomena outside the event horizon, at least for an eternal static configuration. Historically the two most common conceptual models for general relativity have been the "geometric interpretation" (as originially conceived by Einstein) and the "field interpretation" (patterned after the quantum field theories of the other fundamental interactions). These two views are operationally equivalent outside event horizons, but they tend to lead to different conceptions of the limit of gravitational collapse. According to the field interpretation, a clock runs increasingly slowly as it approaches the event horizon (due to the strength of the field), and the natural "limit" of this process is that the clock asymptotically approaches "full stop" (i.e., running at a rate of zero). It continues to exist for the rest of time, but it's "frozen" due to the strength of the gravitational field. Within this conceptual framework there's nothing more to be said about the clock's existence. In contrast, according to the geometric interpretation, all clocks run at the same rate, measuring out real distances along worldlines in curved spacetime. This leads us to think that, rather than slowing down as it approaches the event horizon, the clock is following a shorter and shorter path to the future time coordinates. In fact, the path gets shorter at such a rate that it actually reaches the future infinity of Schwarzschild coordinate time in finite proper time. Now what? If we believe the clock is still running just like every other clock (and there's no local pathology of the spacetime) then it seems natural to extrapolate the clock's existence right past the future infinity of Schwarzschild coordinate time and into another region of spacetime. Obviously this implies that the universe has a non-trivial causal topology, with a one-way boundary, which some people find troubling, but there's nothing logically contradictory about it (in the context of an infinite continuous universe). |
|
|
|
In both of these interpretations we find that an object goes to future infinity (of Schwarzschild coordinate time) as it approaches an event horizon, and its rate of proper time as a function of coordinate time goes to zero. The difference is that the field interpretation is content to truncate its description at the event horizon, while the geometric interpretation carries on with its description right through the event horizon and down to r = 0, where it too finally gives up. What, if anything, is gained by extrapolating the worldlines of infalling objects through the event horizon? One obvious gain is that it offers a prediction of what would be experienced by an infalling observer. Since this represents a worldline that we could, in principle, follow, and since the formulas of relativity continue to make coherent predictions along those worldlines, there doesn't seem to be any compelling reason to truncate our considerations at the horizon. (After all, if we limit our view of the universe to just the worldlines we have followed, or that we intend to follow, we end up with a very oddly shaped universe.) |
|
|
|
By somewhat arbitrarily truncating its descriptions at the event horizon, the "frozen star" interpretation simply declines to consider the metrical extension of the manifold into the region inside the event horizon, which is causally disconnected (in one direction) from the exterior. By declining to consider the fate of infalling worldlines in terms of their own proper times, it avoids dealing with the somewhat awkward issue of a genuine spacetime singularity at r = 0. Therefore, if the "frozen star" interpretation gave equivalent predictions for all externally observable phenomena, and was logically consistent, it might be the preferred view. However, we saw above that the idea of a frozen star as an empty region around which matter "bunches up" outside an event horizon isn't viable, because if nothing ever passes from the exterior to the interior of an event horizon (in a way that is perceivable in finite coordinate time) we cannot accommodate infalling matter. Either the event horizon expands or it doesn't, and in either case we arrive at a contradiction unless the value of m inside the horizon increases, and does so in a way that is perceivable in finite coordinate time. (The fact that the precise location of a horizon depends to some extent on future events doesnít significantly change these considerations.) |
|
|
|
The "trousers topology" described previously is, in some ways, the best of both worlds, but it relies on a somewhat dubious model of material particles as micro singularities in spacetime. We've also seen how the analytical continuation of the external free-fall geodesics into the interior leads to an apparently self-consistent picture of black hole growth in finite coordinate time, and this picture turns out to be fairly isomorphic to the trousers model. (Whether it's isomorphic to the truth is another question.) It may be worthwhile to explicitly describe the situation. Consider a black hole of mass m. The event horizon has radius r = 2m in Schwarzschild coordinates. Now suppose a large concentric spherical dust cloud of total mass m surrounds the black hole is slowly pulled to within a shell of radius, say, 2.1m. The mass of the combined system is 2m, giving it a gravitational radius of r = 4m, and all the matter is now within r = 4m, so there must be, according to the unique spherically symmetrical solution of the field equations, an event horizon at r = 4m. Evidently the dust has somehow gotten inside the event horizon. We might think that although the event horizon has expanded to 4m, maybe the dust is being held "frozen" just outside the horizon at, say, 4.1m. But that can't be true because then there would be only 1m of mass inside the 4m radius, and the horizon would collapse. Also, this would imply that any dust originally inside 4m must have been pushed outward, and there is no known mechanism for that to happen. |
|
|
|
One possible way around this would be for the density of matter to be limited (by some mechanism we don't understand) to just sub-critical. In other words, each spherical region of radius r would be limited to just less than r/2 mass. It might be interesting to figure out the mass density profile necessary to be just shy of having an event horizon at every radius r (possibly inverse square?), but the problem with this idea is that there just isn't any known force that would hold the matter in this configuration. By all the laws we know it would immediately collapse. Of course, it's easy to posit some kind of Pauli-like gravitational "exclusion principle" which would simply prohibit two particles of matter from occupying the same "gravitational state". After all, it's the electron and nucleon exclusion principles that yield the white dwarf and neutron star configurations, respectively. The only reason we end up with black holes is because the universe seems to be one exclusion principle short. Thus, barring any "new physics", there is nothing to prevent an event horizon from forming and expanding, and this implies that the value of m inside the horizon increases in finite coordinate time, which conflicts with the "frozen star" interpretation. |
|
|
|
The preceding discussion makes clear the fact that general relativity is not a relational theory. Schwarzschild spacetime represents a cosmology with a definite preferred frame of reference, the one associated with the time-independent metric components. (Einstein at first was quite disappointed when he learned that the field equations have such an explicitly non-Machian solution, i.e., a single mass in an otherwise empty infinite universe). Of course, we introduced the preferred frame ourselves by imposing spherical symmetry in the first place, but it's always necessary to impose some boundary or initial value conditions, and these conditions (in an open infinite universe) unavoidably single out a particular frame of reference (as discussed further in Section 7.7). That troubled Einstein greatly, and was his main reason for arguing that the universe must be closed, because only in that context can we claim that the entire metric is in some sense fully determined by the distribution of mass-energy. However, there is no precise definition of a black hole in a closed universe, so for the purposes of this discussion we're committed to a cosmology with an arbitrarily preferred frame. |
|
|
|
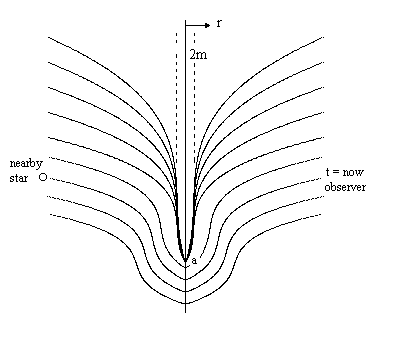
To visualize how this preferred frame effectively governs the physics in Schwarzschild space, consider the following schematic of a black hole: |
|
|
|
|
|
|
|
The star collapsed at point "a", and formed an event horizon of radius 2m in Schwarzschild coordinates. How far is the observer at "O" from the event horizon? If we trace along the spacelike surface "t = now" we find that the black hole doesn't exist at time t = now, which is to say, it is nowhere on the t = now timeslice. The event horizon is in the future of every locus of constant Schwarzschild coordinate time, all the way to future infinity. In fact, the event horizon is part of future null infinity. Nevertheless, the black hole clearly affects the physics on the time foliation t = now at some distance away. For example, if the "observer" at O looks toward the "nearby star", his view will be obstructed, i.e., the star will be eclipsed, because the observer is effectively in the shadow of the infinite future. The size of this shadow will increase as the size of the event horizon increases. |
|
|
|
Thus we can derive knowledge of a black hole from the shadow it casts (like an eclipse), noting that the outline of a shadow isn't subject to speed-of-light restrictions, so there's nothing contradictory about being able to detect the presence and growth of a black hole region in finite coordinate time. Moreover, if the observer is allowed to fall freely, he will go mostly leftward (and slightly up) toward r = 0, quickly carrying him through all future timeslices (which are infinitely compressed around the event horizon) and into the interior. In doing so, he causes the event horizon to expand slightly. |
|
|