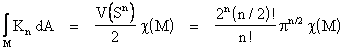7.8 Global Interpretations of Local Experience

I have been standing all my life in the

direct path of a battery of signals,

the most accurately transmitted, most

untranslatable language in the universe…

I am an instrument… trying to translate

 pulsations into images for the relief of the body

and the reconstruction of the mind.

                                         Adrienne Rich, 1971

The usual interpretation of general relativity is based on a conceptual framework consisting of primary entities – such as particles and non-gravitational fields – embedded in an extensive differentiable manifold of space and time. The theory is presented in the form of differential equations, interpreted as giving a description of the local metrical properties of the manifold around any specific point. However, the physically meaningful statements derived from the theory refer to properties of the manifold over extended regions. To produce these statements, the differential equations are integrated (under certain constraints) to give a single coherent extended region of a manifold that everywhere satisfies those equations. This enables us to infer the extended spatio-temporal configurations of fields and particles, from which we derive predictions about observable interactions, which are ultimately reducible to the events of our experience. One question that naturally arises is whether the usual interpretation (or any interpretation) is uniquely singled out by our experience, or whether the same pattern of raw experiences might be explainable within some other, possibly quite different, conceptual framework.

In one sense the answer is obvious. We can always accommodate any sequence of perceptions within an arbitrary ontology merely by positing a suitable theory of appearances separate from our presumed ontology. This approach can be traced back to ancient philosophers such as Parmenides, who taught that motion, change, and even plurality are merely appearances, while the reality is an unchanging unity. Our experience of dreams (for example) shows that the direct correspondence between our perceptions and the events of the external world can always be doubted. Of course, a solipsistic approach to the interpretation of experiences is somewhat repugnant, and need not be taken too seriously, but it nevertheless serves to remind us (if we needed reminding) that the link between our sense perceptions and the underlying external structure is always ambiguous, and any claim that our experiences do (or can) uniquely single out one specific ontology is patently false. There is always a degree of freedom in the selection of our model of the presumed external objective reality.

In more serious models we usually assume that the processes of perception are "of the same kind" as the external processes that we perceive, but we still bifurcate our models into two parts, consisting of (1) an individual's sense impressions and interior experiences, such as thoughts and dreams, and (2) a class of objective exterior entities and events, of which only a small subset correspond to any individual's direct perceptions. Even within this limited class of models, the task of inferring (2) from (1) is not trivial, and there is certainly no a priori requirement that a given set of local experiences uniquely determines a particular global structure. Even if we restrict ourselves to the class of naively realistic models consistent with the observable predictions representable within general relativity, there remains an ambiguity in the conceptual framework.

The situation is complicated by the fact that the field equations of general relativity, by themselves, permit a very wide range of global solutions if no restrictions are placed on the type of boundary conditions, initial values, and energy conditions that are allowed, but most of these solutions are (presumably) unphysical. As Einstein said, "A field theory is not yet completely determined by the system of field equations". In order to extract realistic solutions (i.e., solutions consistent with our experiences) from the field equations we must impose some constraints on the boundary or global topology, and on the allowable form of the “source term”, i.e., energy conditions. In this sense the field equations do not represent a complete theory, because these restrictions can’t be inferred from the field equations; they are auxiliary assumptions that must simply be imposed on the basis of external considerations.

This incompleteness is a characteristic of any physical law that is expressed as a set of differential equations, because such equations generally possess a vast range of possible formal solutions, and require one or more external principle or constraint to yield definite results. The more formal flexibility that our theory possesses, the more inclined we are to ask whether the actual physical content of the theory is contained in the rational "laws" or the circumstantial conditions that we impose. For example, consider a theory consisting of the assertion that certain aspects of our experience can be modeled by means of a suitable Turing machine with suitable initial data. This is a very flexible theoretical framework, since by definition anything that is computable can be computed from some initial data using a suitable Turing machine. Such a theory undeniably yields all applicable and computable results, but of course it also (without further specification) encompasses infinitely many inapplicable results. An ideal theoretical framework would be capable of representing all physical phenomena, but no unphysical phenomena. This is just an expression of the physicist's desire to remove all arbitrariness from the theory. As the general theory of relativity stands at present, it does not yield unique predictions about the overall global shape of the manifold. Instead, it simply imposes certain conditions on the allowable shapes. In this sense we can regard general relativity as a meta-theory, rather than a specific theory.

So, when considering the possibility of alternative interpretations (or representations) of general relativity, we need to decide whether we are trying to find a viable representation of all possible theories that reside within the meta-theory of general relativity, or whether we are trying to find a viable representation of just a single theory that satisfies the requirements of general relativity. The physicist might answer that we need only seek representations that conform with those aspects of general relativity that have been observationally verified, whereas a mathematician might be more interested in whether there are viable alternative representations of the entire meta-theory.

First we should ask whether there are any viable interpretations of general relativity as a meta-theory. This is a serious question, because one plausible criterion for viability is that we can analytically continue all worldlines without leading to any singularities or physical infinities. In other words, an interpretation is considered to be not viable if the representation "breaks down" at some point due to an inability to diffeomorphically continue the solution within that representation. The difficulty here is that even the standard interpretation of general relativity in terms of curved spacetime leads, in some circumstances, to inextendible worldlines and singularities in the field. Thus if we take the position that such attributes are disqualifying, it follows that even the standard interpretation of general relativity in terms of an extended spacetime manifold is not viable.

One possible approach to salvaging the geometrical interpretation would be to adopt, as an additional component of the theory, the principle that the manifold must be free of singularities and infinities. Indeed this principle was often suggested by Einstein, who wrote

It is my opinion that singularities must be excluded. It does not seem reasonable to me to introduce into a continuum theory points (or lines, etc.) for which the field equations do not hold... Without such a postulate the theory is much too vague.

He even hoped that the exclusion of singularities might (somehow) lead to an understanding of atomistic and quantum phenomena within the context of a continuum theory, although he acknowledged that he couldn't say how this might come about. He believed that the difficulty of determining exact singularity-free global solutions of non-linear field equations prevents us from assessing the full content of a non-linear field theory such as general relativity. (He recognized that this was contrary to the prevailing view that a field theory can only be quantized by first being transformed into a statistical theory of field probabilities, but he regarded this as "only an attempt to describe relationships of an essentially nonlinear character by linear methods".)

Another approach, more in the mainstream of current thought, is to simply accept the existence of singularities, i.e., not consider them as a disqualifying feature of an interpretation. According to theorems of Penrose, Hawking, and others, it is known that the existence of a trapped surface (such as the event horizon of a black hole) implies the existence of inextendible worldlines, provided certain energy conditions are satisfied and we exclude closed timelike curves. Therefore, a great deal of classical general relativity and its treatment of black holes, etc., is based on the acceptance of singularities in the manifold, although this is often accompanied with a caveat to the effect that in the vicinity of a singularity the classical field equations may give way to quantum effects.

In any case, since the field equations by themselves undeniably permit solutions containing singularities, we must either impose some external constraint on the class of realistic solutions to exclude those containing singularities, or else accept the existence of singularities. Each of these choices has implications for the potential viability of alternative interpretations. In the first case we are permitted to restrict the range of solutions to be represented, which means we really only need to seek representations of specific theories, rather than of the entire meta-theory represented by the bare field equations. In the second case we need not rule out interpretations based on the existence of singularities, inextendible worldlines, or other forms of "bad behavior".

To illustrate how these considerations affect the viability of alternative interpretations, suppose we attempt to interpret general relativity in terms of a flat spacetime combined with a universal force field that distorts rulers and clocks in just such a way as to match the metrical relations of a curved manifold in accord with the field equations. It might be argued that such a flat-spacetime formulation of general relativity must fail at some point(s) to diffeomorphically map to the corresponding curved-manifold if the latter possesses a non-trivial global topology. For example, the complete surface of a sphere cannot be mapped diffeomorphically to the plane. By means of sterographic projection from the North Pole of a sphere to a plane tangent to the South Pole we can establish a diffeomorphic mapping to the plane of every point on the sphere except the North Pole itself, which maps to a "point at infinity". This illustrates the fact that when mapping between two topologically distinct manifolds such as the plane and the surface of a sphere, there must be at least one point where the mapping is not well-behaved.

However, this kind of objection fails to rule out physically viable alternatives to the curved spacetime interpretation (assuming any viable interpretation exists), and for several reasons. First, we may question whether the mapping between the curved spacetime and the alternative manifold needs to be everywhere diffeomorphic. Second, even if we accede to this requirement, it's important to remember that the global topology of a manifold is sensitive to pointwise excisions. For example, although it is not possible to diffeomorphically map the complete sphere to the plane, it is possible to map the punctured sphere, i.e., the sphere minus one point (such as the North Pole in the sterographic projection scheme). We can analytically continue the mapping to include this point by simply adding a "point at infinity" to the plane - without giving the extended plane intrinsic curvature.

Of course, this interpretation does entail a singularity at one point, where the universal field must be regarded as infinitely strong, but if we regard the potential for physical singularities as disqualifying, then as noted above we have no choice but to allow the imposition of some external principles to restrict the class of solutions to global manifolds that are everywhere "well-behaved". If we also disallow this, then as discussed above there does not exist any viable interpretation of general relativity. Once we have allowed this, we can obviously posit a principle to the effect that only global manifolds which can be diffeomorphically mapped to a flat spacetime are physically permissible. Such a principle is no more in conflict with the field equations than are any of the well-known "energy conditions", the exclusion of closed timelike loops, and so on.

Believers in one uniquely determined interpretation may also point to individual black holes, whose metrical structure of trapped surfaces cannot possibly be mapped to flat spacetime without introducing physical singularities. This is certainly true, but according to theorems of Penrose and Hawking it is precisely the circumstance of a trapped surface that commits the curved-spacetime formulation itself to a physical singularity. In view of this, we are hardly justified in disqualifying alternative formulations that entail physical singularities in exactly the same circumstances.

Another common objection to flat interpretations is that even for a topologically flat manifold like the surface of a torus it is impossible to achieve the double periodicity of the closed torriodal surface, but this objection can also be countered, simply by positing a periodic flat universe. Admittedly this commits us to distant correlations, but such things cannot be ruled out a priori (and in fact distant correlations do seem to be a characteristic of the universe from the standpoint of quantum mechanics, as discussed in Section 9).

More generally, as Poincare famously summarized it, we can never observe our geometry G in a theory-free sense. Every observation we make relies on some prior conception of physical laws P which specify how physical objects behave with respect to G. Thus the universe we observe is not G, but rather U = G + P, and for any given G we can vary P to give the observed U. Needless to say, this is just a simplified schematic of the full argument, but the basic idea is that it's simply not within the power of our observations to force one particular geometry upon us (nor even one particular topology), as the only possible way in which we could organize our thoughts and perceptions of the world. We recall Poincare's famous conventionalist dictum "No geometry is more correct than any other - only more convenient". Those who claim to "prove" that only one particular model can be used to represent our experience would do well to remember John Bell's famous remark that the only thing "proved" by such proofs is lack of imagination.

The interpretation of general relativity as a field theory in a flat background spacetime has a long history. This approach was explored by Feynman, Deser, Weinberg, and others at various times, partly to see if it would be possible to quantize the gravitational field in terms of a spin-2 particle, following the same general approach that was successful in quantizing other field theories. Indeed, Weinberg's excellent "Gravitation and Cosmology" (1972) contained a provocative paragraph entitled "The Geometric Analogy", in which he said

Riemann introduced the curvature tensor R_mnab to generalize the [geometrical] concept of curvature to three or more dimensions. It is therefore not surprising that Einstein and his successors have regarded the effects of a gravitational field as producing a change in the geometry of space and time. At one time it was even hoped that the rest of physics could be brought into a geometric formulation, but this hope has met with disappointment, and the geometric interpretation of the theory of gravitation has dwindled to a mere analogy, which lingers in our language in terms like "metric", "affine connection", and "curvature", but is not otherwise very useful. The important thing is to be able to make predictions about the images on the astronomer's photographic plates, frequencies of spectral lines, and so on, and it simply doesn't matter whether we ascribe these predictions to the physical effect of a gravitational field on the motion of planets and photons or to a curvature of space and time.

The most contentious claim here is that, aside from providing some useful vocabulary, the geometric analogy "is not otherwise very useful". Most people who have studied general relativity have found the geometric interpretation to be quite useful, at least as an aid to understanding the theory, and it obviously seemed useful to Einstein in formulating the theory. Weinberg can hardly have meant to deny this. In context, he was saying that the geometric framework has not proven to be very useful in efforts to unify gravity with the rest of physics. The idea of "bringing the rest of physics into a geometric formulation" refers to attempts to account for the other forces of nature (electromagnetism, strong, and weak) in purely geometrical terms as attributes of the spacetime manifold, as Einstein did for gravity. In other words, to eliminate the concept of "force" entirely, and show that all motion is geodesic in some suitably defined spacetime manifold. This is what is traditionally called a "unified field theory", and led to Weyl's efforts in the 20's, the Kluza-Klein theories, Einstein's anti-symmetric theories, and so on. As Weinberg said, those hopes have (so far) met with disappointment.

In another sense, one might say that all of physics has been subsumed by the geometric point of view. We can obviously describe baseball, music, thermodynamics, etc., in geometrical terms, but that isn't the kind of geometrizing that is being discussed here, i.e., attempts to make the space-time manifold itself account for all the "forces" of nature, as Einstein had made it account for gravity. Quantum field theory works on a background of space-time, but posits other ingredients on top of that to represent the fields. Obviously we're free to construct a geometrical picture in our minds of any gauge theory, just as we can form a geometrical picture in any arbitrary kind of "space", such as the phase space of a system, but this is nothing like what Einstein, Weyl, Kaluza, etc. were talking about. The original (and perhaps naive) hope was to eliminate all other fields besides the metric field of the spacetime manifold itself, to reduce physics to this one primitive entity (and its metric). It's clear that (1) physics has not been geometrized in this sense, viz, with the spacetime metric being the only ontological entity, and (2) in point of fact, some significant progress toward the unification of the other "forces" of nature has indeed been made by people (such as Weinberg himself) who did so without invoking the geometric analogy.

Many scholars have expressed similar views to those of Poincare regarding the essential conventionality of geometry. Even Einstein endorsed those views in a lecture given in 1921, when he said

How are our customary ideas of space and time related to the character of our experiences?  … It seems to me that Poincare clearly recognized the truth in the account he gave in his book “La Science et l’Hypothese”.

In considering the question "Is Spacetime Curved?" Ian Roxburgh described the curved and flat interpretations of general relativity, and concluded that "the answer is yes or no depending on the whim of the answerer. It is therefore a question without empirical content, and has no place in physical inquiry." Thus he agreed with Poincare that our choice of geometry is ultimately a matter of convenience. Even if we believe that general relativity is perfectly valid in all regimes (which most people doubt), it's still possible to place a non-geometric interpretation on the "photographic plates and spectral lines" if we choose. The degree of "inconvenience" is not very great in the weak-field limit, but becomes more extreme if we're thinking of crossing event horizons or circumnavigating the universe. Still, we can always put a non-geometrical interpretation onto things if we're determined to do so. (Ironically, the most famous proponent of the belief that the geometrical view is absolutely essential, indeed a sine qua non of rational thought, was Kant, because the geometry he espoused so confidently was non-curved Euclidean space.)

Even Kip Thorne, who along with Misner and Wheeler wrote the classic text Gravitation espousing the geometric viewpoint, admits that he was once guilty of curvature chauvinism. In his popular book "Black Holes and Time Warps" he writes

Is spacetime really curved? Isn't it conceivable that spacetime is actually flat, but the clocks and rulers with which we measure it... are actually rubbery? Wouldn't... distortions of our clocks and rulers make truly flat spacetime appear to be curved? Yes.

Thorne goes on to tell how, in the early 1970's, some people proposed a membrane paradigm for conceptualizing black holes. He says

When I, as an old hand at relativity theory, heard this story, I thought it ludicrous. General relativity insists that, if one falls into a black hole, one will encounter nothing at the horizon except spacetime curvature. One will see no membrane and no charged particles... the membrane theory can have no basis in reality. It is pure fiction. The cause of the field lines bending, I was sure, is spacetime curvature, and nothing else... I was wrong.

He goes on to say that the laws of black hole physics, written in accord with the membrane interpretation, are completely equivalent to the laws of the curved spacetime interpretation (provided we restrict ourselves to the exterior of black holes), but they are each heuristically useful in different circumstances. In fact, after he got past thinking it was ludicrous, Thorne spent much of the 1980's exploring the membrane paradigm. He does, however, maintain that the curvature view is better suited to deal with interior solutions of black holes, but isn't not clear how strong a recommendation this really is, considering that we don't really know (and aren't likely to learn) whether those interior solutions actually correspond to facts.

Feynman’s lectures on gravitation, written in the early 1960’s, present a field-theoretic approach to gravity, while also recognizing the viability of Einstein’s geometric interpretation. Feynman described the thought process by which someone might arrive at a theory of gravity mediated by a spin-two particle in flat spacetime, analogous to the quantum field theories of the other forces of nature, and then noted that the resulting theory possesses a geometrical interpretation.

It is one of the peculiar aspect of the theory of gravitation that is has both a field interpretation and a geometrical interpretation… the fact is that a spin-two field has this geometrical representation; this is not something readily explainable – it is just marvelous. The geometric interpretation is not really necessary or essential to physics. It might be that the whole coincidence might be understood as representing some kind of gauge invariance. It might be that the relationships between these two points of view about gravity might be transparent after we discuss a third point of view, which has to do with the general properties of field theories under transformations…

He goes on to discuss the general notion of gauge invariance, and concludes that “gravity is that field which corresponds to a gauge invariance with respect to displacement transformations”.

One potential source of confusion when discussing this issue is the fact that the local null structure of Minkowski spacetime makes it locally impossible to smoothly mimic the effects of curved spacetime by means of a universal force. The problem is that Minkowski spacetime is already committed to the geometrical interpretation, because it identifies the paths of light with null geodesics of the manifold. Putting this together with some form of the equivalence principle obviously tends to suggest the curvature interpretation. However, this does not rule out other interpretations, because there are other possible interpretations of special relativity - notably Lorentz's theory - that don't identify the paths of light with null geodesics. It's worth remembering that special relativity itself was originally regarded as simply an alternate interpretation of Lorentz's theory, which was based on a Galilean spacetime, with distortions in both rulers and clocks due to motion. These two theories are experimentally indistinguishable - at least up to the implied singularity of the null intervals. In the context of Galilean spacetime we could postulate gravitational fields affecting the paths of photons, the rates of physical clocks, and so on. Of course, in this way we arrive at a theory that looks exactly like curved spacetime, but we interpret the elements of our experience differently. Since (in this interpretation) we believe light rays don't follow null geodesic paths (and in fact we don't even recognize the existence of null geodesics) in the "true" manifold under the influence of gravity, we aren't committed to the idea that the paths of light delineate the structure of the manifold. Thus we'll agree with the conventional interpretation about the structure of light cones, but not about why light cones have that structure.

At some point any flat manifold interpretation will encounter difficulties in continuing its worldlines in the presence of certain postulated structures, such as black holes. However, as discussed above, the curvature interpretation is not free of difficulties in these circumstances either, because if there exists a trapped surface then there also exist non-extendable timelike or null geodesics for the curvature interpretation. So, the (arguably) problematical conditions for a "flat space" interpretation are identical to the problematical conditions for the curvature interpretation. In other words, if we posit the existence of trapped surfaces, then it's disingenuous for us to impugn the robustness of flat space interpretations in view of the fact that these same circumstances commit the curvature interpretation to equally disquieting singularities.

It may or may not be the case that the curvature interpretation has a longer reach, in the sense that it's formally extendable inside the Schwarzschild radius, but, as noted above, the physicality of those interior solutions is not (and probably never will be) subject to verification, and they are theoretically controversial even within the curvature tradition itself. Also, the simplistic arguments proposed in introductory texts are easily seen to be merely arguments for the viability of the curvature interpretation, even though they are often mis-labeled as arguments for the necessity of it.

There's no doubt that the evident universality of local Lorentz covariance, combined with the equivalence principle, makes the curvature interpretation eminently viable, and it's probably the "strongest" interpretation of general relativity in the sense of being exposed most widely to falsification in principle, just as special relativity is stronger than Lorentz’s ether theory. The curvature interpretation has certainly been a tremendous heuristic aid (maybe even indispensable) to the development of the theory, but the fact remains that it isn't the only possible interpretation. In fact, many (perhaps most) theoretical physicists today consider it likely that general relativity is really just an approximate consequence of some underlying structure, similar to how continuum fluid mechanics emerges from the behavior of huge numbers of elementary particles. As was rightly noted earlier, much of the development of particle physics and more recently string theory has been carried out in the context of rather naive-looking flat backgrounds. Maybe Kant will be vindicated after all, and it will be shown that humans really aren't capable of conceiving of the fundamental world on anything other than a flat geometrical background. If so, it may tell us more about ourselves than about the world.

Another potential source of confusion is the tacit assumption on the part of some people that the topology of our experiences is unambiguous, and this in turn imposes definite constraints on the geometry via the Gauss-Bonnet theorem. Recall that for any two-dimensional manifold M the Euler characteristic is a topological invariant defined as

where V, E, and F denote the number of vertices, edges, and faces respectively of any arbitrary triangulation of the entire surface. Extending the work that Gauss had done on the triangular excess of curves surfaces, Bonnet proved in 1858 the beautiful theorem that the integral of the Gaussian curvature K over the entire area of the manifold is proportional to the Euler characteristic, i.e.,

More generally, for any manifold M of dimension n the invariant Euler characteristic is

where ν_k is the number of k-simplexes of an arbitrary "triangulation" of the manifold. Also, we can let K_n denote the analog of the Gaussian curvature K for an n-dimensional manifold, noting that for hypersurfaces this is just the product of the n principal extrinsic curvatures, although like K it has a purely intrinsic significance for arbitrary embeddings. The generalized Gauss-Bonnet theorem is then

where V(Sⁿ) is the "volume" of a unit n-sphere. Thus if we can establish that the topology of the overall spacetime manifold has a non-zero Euler characteristic, it will follow that the manifold must have non-zero metrical curvature at some point. Of course, the converse is not true, i.e., the existence of non-zero metrical curvature at one or more points of the manifold does not imply non-zero Euler characteristic. The two-dimensional surface of a torus with the usual embedding in R³ not only has intrinsic curvature but is topologically distinct from R², and yet (as discussed in Section 7.5) it can be mapped diffeomorphically and globally to an everywhere-flat manifold embedded in R⁴. This illustrates the obvious fact that while topological invariants impose restrictions on the geometry, they don't uniquely determine the geometry.

Nevertheless, if a non-zero Euler characteristic is stipulated, it is true that any diffeomorphic mapping of this manifold must have non-zero curvature at some point. However, there are two problems with this argument. First, we need not be limited to diffeomorphic mappings from the curved spacetime model, especially since even the curvature interpretation contains singularities and physical infinities in some circumstances. Second, the topology is not stipulated. The topology of the universe is a global property which (like the geometry) can only be indirectly inferred from local experiences, and the inference is unavoidably ambiguous. Thus the topology itself is subject to re-interpretation, and this has always been recognized as part-and-parcel of any major shift in geometrical interpretation. The examples that Poincare and others talked about often involved radical re-interpretations of both the geometry and the topology, such as saying that instead of a cylindrical dimension we may imagine an unbounded but periodic dimension, i.e., identical copies placed side by side. Examples like this aren't intended to be realistic (necessarily), but to convey just how much of what we commonly regard as raw empirical fact is really interpretative.

We can always save the appearances of any particular apparent topology with a completely different topology, depending on how we choose to identify or distinguish the points along various paths. The usual example of this is a cylindrical universe mapped to an infinite periodic universe. Therefore, we cannot use topological arguments to prove anything about the geometry. Indeed these considerations merely extend the degrees of freedom in Poincare's conventionalist formula, from U = G + P to U = (G + T) + P, where T represents topology. Obviously the metrical and topological models impose consistency conditions on each other, but the two of them combined do not constrain U any more than G alone, as long as the physical laws P remain free.

There may be valid reasons for preferring not to avail ourselves of any of the physical assumptions (such as a "universal force", let alone multiple copies of regions, etc.) that might be necessary to map general relativity to a flat manifold in various (extreme) circumstances, such as in the presence of trapped surfaces or other "pathological" topologies, but these are questions of convenience and utility, not of feasibility. Moreover, as noted previously, the curvature interpretation itself entails inextendable worldlines as soon as we posit a trapped surface, so topological anomalies hardly give an unambiguous recommendation to the curvature interpretation.

The point is that we can always postulate a set of physical laws that will make our observations consistent with just about any geometry we choose (even a single monadal point!), because we never observe geometry directly. We only observe physical processes and interactions. Geometry is inherently an interpretative aspect of our understanding. It may be that one particular kind of geometrical structure is unambiguously the best (most economical, most heuristically robust, most intuitively appealing, etc), and any alternative geometry may require very labored and seemingly ad hoc "laws of physics" to make it compatible with our observations, but this simply confirms Poincare's dictum that no geometry is more true than any other - only more convenient.

It may seem as if the conventionality of geometry is just an academic fact with no real applicability or significance, because all the examples of alternative interpretations that we've cited have been highly trivial. For a more interesting example, consider a mapping (by radial projection) from an ordinary 2-sphere to a circumscribed polyhedron, say a dodecahedron. With the exception of the 20 vertices, where all the "curvature" is discretely concentrated, the surface of the dodecahedron is perfectly flat, even along the edges, as shown by the fact that we can "flatten out" two adjacent pentagonal faces on a plane surface without twisting or stretching the surfaces at all. We can also flatten out a third pentagonal face that joins the other two at a given vertex, but of course (in the usual interpretation) we can't fit in a fourth pentagon at that vertex, nor do three quite "fill up" the angular range around a vertex in the plane. At this stage we would conventionally pull the edges of the three pentagons together so that the faces are no longer coplanar, but we could also go on adjoining pentagonal surfaces around this vertex, edge to edge, just like a multi-valued "Riemann surface" winding around a pole in the complex plane. As we march around the vertex, it's as if we are walking up a spiral staircase, except that all the surfaces are laying perfectly flat. This same "spiral staircase" is repeated at each vertex of the solid.

Naturally we can replace the dodecahedron with a polyhedron having many more vertices, but still consisting of nothing but flat surfaces, with all the "curvature" distributed discretely at a huge number of vertices, each of which is a "pole" of an infinite spiral staircase of flat surfaces. This structure is somewhat analogous to a "no-collapse" interpretation of quantum mechanics, and might be called a "no-curvature" interpretation of general relativity. At each vertex (cf. measurement) we "branch" into on-going flatness across the edge, never actually "collapsing" the faces meeting at a vertex into a curved structure. In essence the manifold has zero Euler characteristic, but it exhibits a non-vanishing Euler characteristic modulo the faces of the polyhedron. Interestingly, the term "branch" is used in multi-valued Riemann surfaces just as it's used in some descriptions of the "no-collapse" interpretation of quantum mechanics. Also, notice that the non-linear aspects of both theories are (arguably) excised by this maneuver, leaving us "only" to explain how the non-linear appearances emerge from this aggregate, i.e., how the different moduli are inter-related. To keep track of a particle we would need its entire history of "winding numbers" for each vertex of the entire global manifold, in the order that it has encountered them (because it's not commutative), as well as it's nominal location modulo the faces of the polyhedron.

In this model the full true topology of the universe is very different from the apparent topology modulo the polyhedral structure, and curvature is non-existent on the individual branches, because every time we circle a non-flat point we simply branch to another level (just as in some of the no-collapse interpretations of quantum mechanics the state sprouts a new branch, rather than collapsing, each time an observation is made). Each time a particle crosses an edge between two vertices it's set of winding numbers is updated, and we end up with a combinatorial approach, based on a finite number of discrete poles surrounded by infinitely proliferating (and everywhere-flat) surfaces. We can also arrange for the spiral staircases to close back on themselves after a suitable number of windings, while maintaining a vanishing Euler characteristic.

For a less outlandish example of a non-trivial alternate interpretation of general relativity, consider the "null surface" interpretation. According to this approach we consider only the null surfaces of the traditional spacetime manifold. In other words, the only intervals under consideration are those such that g_μν dx^μ dx^ν = 0. Traditional timelike paths are represented in this interpretation by zigzag sequences of lightlike paths, which can be made to approach arbitrarily closely to the classical timelike paths. The null condition implies that there are really only three degrees of freedom for motion from any given point, because given any three of the increments dx⁰, dx¹, dx², and dx³, the corresponding increment of the fourth automatically follows (up to sign). The relation between this interpretation and the conventional one is quite similar to the relation between special relativity and Lorentz's ether theory. In both cases we can use essentially the same equations, but whereas the conventional interpretation attributes ontological status to the absolute intervals dt, the null interpretation asserts that those absolute intervals are ultimately superfluous conventionalizations (like Lorentz's ether), and encourages us to dispense with those elements and focus on the topology of the null surfaces themselves.

Return to Table of Contents