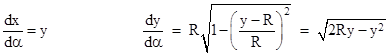I first have to learn to watch very respectfully as the masters of creativity perform their intellectual climbing feats, while I stay bowleggedly below in the valley mist. I already have a premonition that up there the sun is always shining!

Hedwig Born to Einstein, 1919

The curve traced out by a point on the rim of a rolling circle is called a cycloid, and we've seen that this curve describes gravitational free-fall, both in Newtonian mechanics and in general relativity (in terms of the free-falling proper time). Interestingly, this class of curves was a significant object of study for several important scientists, and was called "the Helen of geometers" because of all the disputes it provoked. It was first discussed by Charles Bouvelles in 1501 as a mechanical means of squaring the circle. Subsequently Galileo and his student Viviani studied the curve, finding a method of constructing tangents, and Galileo suggested that it might be a suitable shape for an arch bridge.

Mersenne publicized the cycloid among his group of correspondents, including the young Roberval, who, by the 1630's had determined many of the major properties of the cycloid, such as the interesting fact that the area under a complete cycloidal arch is exactly three times the area of the rolling circle. Roberval used his problem-solving techniques in 1634 to win the Mathematics chair at the College Royal, which was determined every three years by an open competition. Unfortunately, the contest did not require full disclosure of the solution methods, so the incumbent (who selected the contest problems) had a strong incentive to keep his best methods a secret, lest they be used to unseat him at the next contest. In retrospect, this was not a very wise arrangement for a teaching position. Roberval held the chair for 40 years, but by keeping his solution methods secret he lost priority for several important discoveries, and became involved in numerous quarrels. One of the men accused by Roberval of plagiarism was Torricelli, who in 1644 was the first to publish an explanation of the area and the tangents of the cycloid. It's now believed that Torricelli arrived at his results independently. (Torricelli served as Galileo's assistant for a brief time, and probably first learned of the cycloid from him.)

In 1658, four years after renouncing mathematics as a vainglorious pursuit, Pascal found himself one day suffering from a painful toothache, and in desperation began to think about the cycloid to take his mind off the pain. Quickly the pain abated, and Pascal interpreted this as a sign from the Almighty that he should proceed to study the cycloid, which he did intensively for the next eight days. During this period he rediscovered most of what had already been learned about the cycloid, and several results that were new. Pascal decided to propose a set of challenge problems, with the promise of a first and second prize to be awarded for the best solutions. Roberval was named as one of the judges. Only two sets of solutions were received, one from Antoine de Lalouvere and another from John Wallis, but Pascal and Roberval decided that neither of the entries merited a prize, so no prizes were awarded. Instead, Pascal published his own solutions, along with an essay on the "History of the Cycloid", in which he essentially took Roberval's side in the priority dispute with Torricelli.

The conduct of Pascal's cycloid contest displeased many people, but it had at least one useful side effect. In 1658 Christiaan Huygens was thinking about how to improve the design of clocks, and of course he realized that the period of oscillation of a simple pendulum (i.e., a massive object constrained to moving along a circular arc under the vertical force of gravity) is not perfectly independent of the amplitude. Prompted by Pascal's contest, Huygens decided to consider how an object would oscillate if constrained to follow an upside-down cycloidal path, and found to his delight that the frequency of such a system actually is perfectly independent of the amplitude. Thus he had discovered that the cycloid is the tautochrone, i.e., the curve for which the time taken by a particle sliding from any point on the curve to the lowest point on the curve is the same, independent of the starting point. He presented this result in his great treatise "Horologium Oscillatorium" (not published until 1673), in which he clearly described the modern principle of inertia (the foundation of relativity), the law of centripetal force, the conservation of kinetic energy, and many other important concepts of dynamics - ten years before Newton's "Principia".

The cycloid went on attracting the attention of the world's best mathematicians, and revealing new and remarkable properties. For example, in June of 1696, Jean (aka Johann, John) Bernoulli issued the following challenge to the other mathematicians of Europe:

If two points A and B are given in a vertical plane, to assign to a mobile particle M the path AMB along which, descending under its own weight, it passes from the point A to the point B in the briefest time.

Pictorially the problem is as shown below:

In accord with its defining property, the requested curve is called the brachistochrone. The first satisfactory solution was first found by Jean and/or his older brother Jacques (aka Jakob, James) Bernoulli, depending on whom you believe. (Each of the brothers worked on the problem, and there were later accusations of plagiarism.) Jean, who was not inclined to under-state the significance of his discoveries, revealed his solution in January of 1697 by first reminding his readers of Huygens' tautochrone, and then saying "you will be petrified with astonishment when I say that precisely this same cycloid... is our required brachistochrone".

Jean arrived at his solution by making a direct analogy between the motion of a material particle subject to the acceleration of gravity and the motion of a pulse of light through a medium with varying index of refraction. Recall that Fermat’s principle of least time signifies that a pulse of light follows the path of least time between two given points, depending on how the speed of the pulse varies along the path. He wrote

Whether the increase in the velocity depends on the nature of the medium, more or less resistant, as in the case of the ray of light, or whether one removes the medium, and supposes that the acceleration is produced by means of another agency but according to the same law, as in the case of gravity; since in both cases the curve is in the end supposed to be traversed in the shortest time, what hinders us from substituting the one in place of the other?

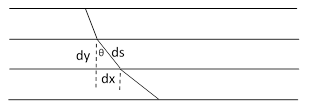
Accordingly, Bernoulli considered the path of a pulse of light passing through layers of a medium with varying indices of refraction, as illustrated below.

By Snell’s law, the quantity n sin(θ) is constant for all the layers, where n is the index of refraction of a given layer and θ is the angle of the path (relative to vertical) in that layer. Noting that sin(θ) = dx/ds, and that n is proportional to the inverse of the velocity v, it follows that for some constant k we have

Now, since (ds)² = (dx)² + (dy)², we have

For a particle of mass m falling from rest at a height y = 0, the velocity v is a function of the “height” y according to the relation equating the change in potential energy with the change in kinetic energy, i.e., we have

where g is the acceleration of gravity and noting that we are taking y as positive in the downward direction. Choosing k = 2g we have v² = ky, so the differential equation can be written as

Bernoulli notes that this is the differential equation for a cycloid, i.e., the path traced by a point on the perimeter of a circle as the circle rolls along a flat surface. This can be verified by differentiating the parametric cycloid expressions

from which we get

and hence

so the brachistochrone formula represents a cycloid for a circle of diameter k. Thus Bernoulli showed how this problem is related in general to the mechanical problem of an object moving with varying speeds due to any cause. "In this way", he wrote, "I have solved two important problems - an optical and a mechanical one...". He was also impressed by the fact that this concordance was valid only because Galileo's law of falling bodies has the form that it does, i.e., the speeds of two falling bodies are to each other as the square roots of the altitudes traveled. He concluded

Before I end I must voice once more the admiration I feel for the unexpected identity of Huygens' tautochrone and my brachistochrone. I consider it especially remarkable that this coincidence can take place only under the hypothesis of Galileo, so that we even obtain from this a proof of its correctness. Nature always tends to act in the simplest way, and so it here lets one curve serve two different functions, while under any other hypothesis we should need two curves...

Presumably his enthusiasm would have been even greater had he known that the same curve describes radial gravitational freefall versus proper time in general relativity. We see from Bernoulli’s work that the variational techniques developed to solve problems like the brachistochrone also found physical application in what came to be called the principle of least action, a principle usually attributed to Maupertius, or perhaps Leibniz (if one accepts the contention that “the best of all possible worlds” represents an expression of this principle). Fermat’s principle of least time for light rays, as discussed in Section 3.4, is just one particularly striking application of this variational approach. Essentially the same technique is used to determine the equations of a geodesic path in the curved spacetime of general relativity.

Incidentally, the Bernoulli's were partisans on the side of Leibniz in the famous priority dispute between Leibniz and Newton over the invention of calculus. Before revealing his solution to the brachistochrone challenge problem, Jean Bernoulli along with Leibniz sent a copy of the challenge directly to Newton in England, and included in the public announcement of the challenge the words

...there are fewer who are likely to solve our excellent problems, aye, fewer even among the very mathematicians who boast that [they]... have wonderfully extended its bounds by means of the golden theorems which (they thought) were known to no one, but which in fact had long previously been published by others.

It seems clear the intent was to humiliate the aging Newton (who by then had left Cambridge and was Warden of the Mint), by demonstrating that he was unable to solve a problem that Leibniz and the Bernoullis had solved. The story as recounted by Newton's biographer Conduitt is that Sir Isaac "in the midst of the hurry of the great recoinage did not come home till four from the Tower very much tired, but did not sleep till he had solved it, which was by 4 in the morning." In all, Bernoulli received only three solutions to his challenge problem, one from Leibniz, one from l'Hospital, and one anonymous solution from England. Bernoulli supposedly said he knew who the anonymous author must be, "as the lion is recognized by his print". Newton was obviously proud of his solution, although he commented later that "I do not love to be dunned & teezed by forreigners about Mathematical things..."

In the twentieth century, Planck was the most prominent enthusiast for the variational approach, asserting that “the principle of least action is perhaps that which, as regards form and content, may claim to come nearest to that ideal final aim of theoretical research”. Indeed he even (at times) argued that the principle manifests a deep teleological aspect of nature, since it can be interpreted as a global imperative, i.e., systems evolve locally in a way that extremizes (or makes stationary) certain global measures in a temporally symmetrical way, as if the final state were already determined. He wrote

In fact, the least-action principle introduces an entirely new idea into the concept of causality: The causa efficiens, which operates from the present into the future and makes future situations appear as determined by earlier ones, is joined by the causa finalis for which, inversely, the future – namely, a definite goal – serves as the premise from which there can be deduced the development of the processes which lead to this goal.

It’s surprising to see this called “an entirely new idea”, considering that causa finalis was among the four fundamental kinds of causation enunciated by Aristotle. In any case, throughout his life the normally austere and conservative Planck continued to have an almost mystical reverence for the principle of least action, arguing that it is not only “the most comprehensive of all physical laws”, but that it actually represents the purest expression of the thoughts of God.

Interestingly, Fermat himself was much less philosophically committed to the principle that he himself originated (somewhat like Einstein’s ambivalence toward the quantum theory). After being challenged on the fundamental truth of the "least time" principle as a law of nature by the Cartesian Clerselier, Fermat replied in exasperation

I do not pretend and I have never pretended to be in the secret confidence of nature. She moves by paths obscure and hidden...

Fermat was content to regard the principle of least time as a purely abstract mathematical theorem, describing – though not necessarily explaining – the behavior of light.

Return to Table of Contents