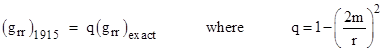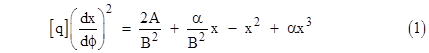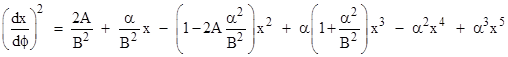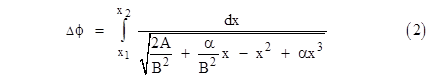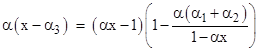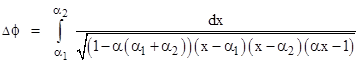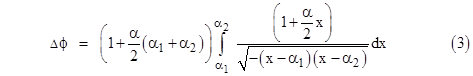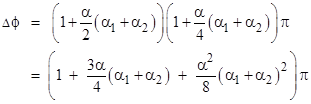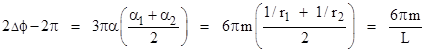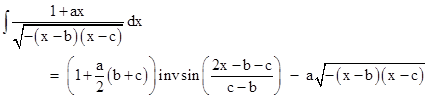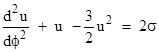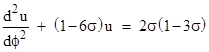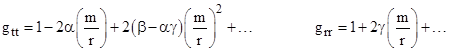8.10  Conquering the Perihelion

O you who by the light of nature arouse in us a longing for the light of grace, so by means of that you can transport us into the light of glory; I give thanks to you, because you have lured me into the enjoyment of your work, and I have exulted in the works of your hands; behold, now I have consummated the work to which I pledged myself, using all the abilities that you gave to me…

                                                                Johannes Kepler, 1618

On 18 November, 1915, shortly before arriving at the final field equations of general relativity, Einstein published a derivation of Mercury’s orbital precession based on the vacuum field equations, which turned out to carry over unchanged in the final theory. As early as 1907 he had written to Conrad Habicht that he was working in a theory of gravitation that he hoped would account for the anomalous precession of Mercury. Now, eight years later, he was finally was able to derive this result. He told a friend that he was beside himself with excitement for several days after establishing this agreement between theory and observation. The derivation he published in 1915 is mathematically interesting, not just for how he inferred the equation of motion from the vacuum field equations (without the benefit of the Schwarzschild metric), but also for his method of inferring the amount of precession from this equation. In reference to this derivation, the great mathematician David Hilbert, who at the time was working on a unified field theory based in part on Einstein’s nascent gravitational theory, wrote enviously to Einstein

… congratulations on conquering perihelion motion. If I could calculate as rapidly as you, in my equations the electron would correspondingly have to capitulate, and simultaneously the hydrogen atom would have to produce its note of apology about why it does not radiate.

Hilbert may not have been aware of it, but Einstein had an advantage in “conquering” the perihelion calculation so rapidly, because he had performed the same calculation previously (together with his friend Michele Besso) based on earlier versions of his theory. From the theoretical standpoint the important part of this work was obviously deriving the equation of motion, but from a purely mathematical standpoint, in order to quantitatively compare the results with observation, the determination of the implied perihelion precession rate was also important. This step introduced no novel concepts, but it was not an entirely trivial exercise. The “quadrature” approach taken by Einstein is not followed by most modern texts (an exception being Weinberg, 1972), so it’s interesting to review the paper of 18 November 1915 paper to see exactly how he did it. His explanation is rather terse (and there are a couple of typos in the published paper), so it takes a bit of effort to reconstruct his reasoning.

First we should reiterate that Einstein did not arrive at the final form of the field equations (with the “trace” term) until November 25th, but the perihelion motion depends only on the vacuum solution, which is unaffected by the trace term, so its absence didn’t invalidate the November 18 results on Mercury’s precession. Second, not only was Einstein not in possession of the full field equations, he didn’t yet know the exact spherically symmetrical vacuum solution, something which was found by Schwarzschild less than a month later (working at his post on the Russian front, as discussed in Section 8.7). For this reason, Einstein worked with just an approximation to the spherically symmetrical solution of the (vacuum) field equations. He gave this metric in terms of a Cartesian coordinate system, but essentially his approximate metric can be written in polar coordinates as

Schwarzschild soon showed that the coefficient of (dr)² should really be (1 − 2m/r)⁻¹, which agrees with Einstein’s approximation only to the first order in m/r. Given the high degree of symmetry in this case, it actually isn’t difficult to determine the exact solution from the field equations (or even from Kepler’s third law, as discussed in Section 5.5), but Einstein hadn’t expected any simple exact solution to exist, so he hadn’t looked very hard. (He replied to Schwarzschild’s letter “I would not have thought that the strict treatment of the mass-point problem was so simple”.) His approximate metric coefficient g_rr is related to the exact Schwarzschild g_rr by

Thus the coefficients differ in the second order in 2m/r. Using his approximate metric for the spherically symmetrical vacuum field, Einstein evaluated the Christoffel symbols to determine the geodesic equations of motion, and arrived (just as in modern derivations) at the equation

where x = 1/r is the inverse of the radial distance from the Sun, ϕ is the angular coordinate in the orbital plane, the symbols A and B are constants of integration (B is the angular momentum and A is related to the energy), and α = 2m where m is the Sun’s mass in geometrical units. If we use the exact Schwarzschild metric, this equation is exact with q = 1, but with Einstein’s approximate metric the value of q should actually be 1 – α²x². Dividing through by q, or, what amounts to nearly the same thing, multiplying through by 1 + α²x², the actual equation (1) based on Einstein’s approximate metric would be

Fortunately Einstein recognized that he could take q = 1 without affecting the lowest-order non-Newtonian effect, so he proceeded to use equation (1) with q = 1, which happens to be exactly correct, even though he thought it was an approximation.

From this point most modern derivations differentiate equation (1) again with respect to ϕ, leading to a second order “harmonic” equation with a small relativistic correction term, from which the perihelion precession can be inferred, at least for sufficiently small eccentricity (as discussed later in this section). However, this is not how Einstein proceeded. Instead, he took the square root of the reciprocal of both sides of the above equation, giving the elliptic integral for the angular travel Δϕ between any two inverse radial parameters x₁ and x₂

(Incidentally, if we integrated over r instead of x, we would get a factor of r² in the denominator, due to the fact that dx = −dr/r².) Determining the explicit expression for an elliptic integral in terms of elementary functions is not generally possible, so this approach may seem unpromising, but Einstein was able to approximate the integral with the necessary degree of accuracy. To do this, he made use of the fact that the relevant limits of integration to find the angular travel between apogee and perigee are the values of x at which the derivative of r with respect to ϕ vanishes. Hence we need to integrate between two roots of the cubic under the square root. As in Einstein’s paper, let α₁ and α₂ denote these two roots. We will also let α₃ denote the third root, so the polynomial under the square root can be written as

Also, since the coefficient of x² in the monic polynomial on the left side is −1/α, we have

Consequently the product of α and (x – α₃) can be written as

Furthermore, noting that all the quantities αx, αα₁, and αα₂ are all extremely small compared with 1 (because each of them is roughly twice the Sun’s mass in geometrical units, which is less than 1.5 km, divided by the radius of Mercury’s orbit, which is over 55 million km), we see that the denominator 1 − αx in the second factor on the right hand side represents a correction on the order (αx)² to the overall factor, so it is negligible. Hence with sufficient accuracy we can write

and therefore the elliptic integral from apogee to perigee can be written as

Now, making use of the approximation (1−z)^−1/2 ≈ 1 + z/2 for small z, we can bring the constant factor outside the integral, and raise the final factor, so the equation can be written in the form

The definite integral can be evaluated in closed form, giving the result

This is the arc length from the apogee to the next perigee, and equivalently from the perigee to the next apogee, so the total arc length for one “cycle” from one perihelion to the next is twice this amount, and if we subtract 2π we get the precession per cycle. The third term is negligible, so we have the result

where L is the semi-latus rectum of the orbital ellipse. Inserting the values for the Sun’s mass in geometrical units (1.475 km) and the semi-latus rectum of Mercury’s orbit (55.4430 million km) gives 0.1034 arc seconds per revolution, and since Mercury completes 414.9378 revolutions per century, we get 42.9195 arc seconds per century, which agrees very closely with the observed value.

This derivation might seem to rely on knowledge of the arcane indefinite integral

but, as explained in Section 6.2, this is not really needed, because the denominator of the integrand reduces to unity when we change to the angular variable α defined by

The variable x ranges from b to c as the variable α ranges from 0 to π. There is nothing mysterious about this substitution, since it is simply the equation of an ellipse, and the same substitution is already used in the Newtonian case.

Despite the simplicity of this approach, and the fact that it can be immediately extended to arbitrary accuracy, including the effect of eccentricity (as described in Section 6.2), several other methods have also been used to derive the relativistic precession. Perhaps the most common is to differentiate equation (11) of Section 6.2 again with respect to ϕ and divide through by 2(du/dϕ) to give the second order differential equation

where u = 2m/r and σ = (m/h)². This differs from the Newtonian equation only by the term −(3/2)u², which makes the equation non-linear. However, for orbits that are nearly circular (i.e., only slight variations in u), we can linearize this equation. Over any infinitesimal range u₀ ± Δu the quantity u − (3/2)u² can be represented by a linear function with slope equal to the derivative of this quantity at u₀. Thus over this incremental range we can set u − (3/2)u² = (1−3u₀)u + (3/2)u₀², and hence, noting that (by Kepler’s law) u₀ is approximately 2σ in the limit as the eccentricity approaches zero, the equation of motion takes the linear form

This represents a simple harmonic oscillator with the well-known solution u(ϕ) = K[1+ ε cos(Ωϕ)] where ε is a constant of integration and

The radial parameter returns to its original value when Ωϕ = 2π, so the angular travel for one radial cycle is 2π/Ω, whereas the angular travel for one angular cycle is simply 2π. As a result, the perihelion precesses by the amount

on each revolution, noting that σ ≈ m/L. The shortcoming of this method is that it strictly applies only for nearly circular orbits, whereas Einstein’s method (when carried out fully as in Section 6.2) shows that the result applies to any eccentricity.

At the conclusion of his letter of 22 December 1915 informing Einstein of the exact spherically symmetrical metric, which he had been prompted to seek while studying Einstein’s paper on Mercury’s precession, Schwarzschild wrote

It is a wonderful thing that the explanation for the Mercury anomaly emerges so convincingly from such an abstract idea.

The agreement between general relativity and the precession of Mercury’s orbit was, and remains, one of the strongest confirmations of Einstein’s theory because, of all the classical tests, it alone is sensitive to the second-order in m/r. The equivalence principle by itself strongly suggests that gravity can be modeled by a metrical theory of spacetime (in which particles follow stationary paths), but it does not necessarily single out Einstein’s field equations as the laws governing the metric. In general we can only say that each diagonalized coefficient of the metric in the vicinity of a spherically symmetrical gravitating body should be expressible (at least in the weak field) as a power series in m/r. In terms of the usual Schwarzschild coordinates r and t the conventional way of writing this parameterized post-Newtonian (PPN) metric is

where

for constants α, β and γ. The constant α is directly measurable in terms of the gravitational acceleration experienced by a static object in the weak field limit, and since we define the mass of an object on this basis, we effectively define α = 1 in any theory that satisfies the equivalence principle. The other two parameters, β and γ, are dependent on the field equations of whatever theory of gravity we choose. Einstein’s field equations of general relativity give these constants the values β = γ = 1, but in other metrical theories of gravity these constants have different values.

Of the three classical tests of general relativity, the gravitational redshift depends only on g_tt and can only be evaluated up to the first order, so it really verifies only the fact that α = 1, which is to say, it verifies only the equivalence principle. Needless to say, this is an important verification, but it doesn’t single out Einstein’s field equations as opposed to the field equations of other possible metric theories. The second classical test was the deflection of starlight grazing the Sun during a solar eclipse, and it can be shown that this test verifies not only α = 1, it also depends on g_rr up to the first order, so it verifies γ = 1 as well. Likewise the “Shapiro test” based on the time delay of radar echoes from the inner planets allows us to evaluate α and γ, but none of these tests enable us to evaluate the g_tt coefficient to the second order, i.e., they do not constrain the value of β.

However, according to the general metrical theory, the precession per revolution of an orbit with semi-latus rectum L is 6πm/L times the factor (2 − β + 2γ)/3. Since the precession of Mercury’s orbit is in close agreement with the value 6πm/L, and since we can determine γ = 1 by other means, we can conclude that β = 1, consistent with Einstein’s field equations. Thus the perihelion observations are among the strongest confirmations we have of the validity of general relativity.

Because of the importance of this observational verification, it’s of interest to know whether, or how much, Einstein was influenced or guided by knowledge of Mercury’s precession in the formulation of general relativity. Throughout the years from 1908 to 1914 while he was working on the theory, he often assessed the redshift and the starlight deflection predictions of his current theory, but he never mentioned (in print) the precession of Mercury. Only when he presented his completed theory late in 1915 was the agreement with Mercury’s precession cited. Nevertheless, we know Einstein was quite conscious of the Mercury precession anomaly throughout the years when he was developing general relativity. Furthermore, he was not alone in his interest in this seemingly obscure anomaly. For example, Henri Poincare wrote about the anomaly in his 1908 book Science and Method. In the section entitled “The New Mechanics and Astronomy” he notes that for a theory of gravity with a velocity dependent potential (along the lines suggested by Weber for electromagnetism)

there would result, in the perihelion of Mercury, a secular variation of 14” [seconds of arc per century], in the same direction as that which has been observed and not explained, but smaller, since the latter is 38”.

He goes on to say that Lorentz’s theory of relativity (and therefore also Einstein’s special relativity, although Poincare never mentioned Einstein in connection with relativity) predicts an advance of 7” seconds of arc per century for Mercury’s perihelion. He concludes that

This cannot be regarded as an argument in favor of the new dynamics, since we still have to seek another explanation of the greater part of the anomaly connected with Mercury, but still less can it be regarded as an argument against it.

This is interesting because it clearly shows that, at least in Poincare’s mind, there was an anomaly connected with Mercury, and moreover that this anomaly was roughly 38”. According to some accounts (e.g., Roseveare) there was no pressing anomaly perceived at this time, because Seeliger’s hypothesis (1906) of a solar corona was thought to be adequate to account for the extra precession of Mercury’s orbit. Roseveare says

I think that the reason for … the general neglect of the perihelion of Mercury as an anomaly to be explained by any new gravitational theory [in 1913] was that Seeliger’s hypothesis was being taken very seriously… Since it was felt by both Einstein and Nordstrom that no empirical argument existed beyond the light deflection predictions, one can only assume that the perihelion motion of Mercury was not considered to be anomalous and that the prevailing hypothesis explaining it, Seelinger’s hypothesis, was valid.

According to this account, the paper written by Einstein’s friend Freundlich in February 1915 arguing against Seeliger’s hypothesis was motivated by a desire to restore the precession of Mercury’s orbit to the status of an anomaly so that it could be used as a test of gravitational theories. This seems like rather odd reasoning, and Roseveare himself admits that his argument is undermined by Einstein’s later comment (in 1916) that Freundlich’s attack on Seeliger’s hypothesis was “forcing an open door”, which clearly implies that Einstein (like Poincare) did not take Seeliger’s hypothesis seriously.

Admittedly in 1906 (the year Seeliger published his hypothesis), Poincare stated that although the extra precession in Mercury’s orbit was at that time the most grave discordance known for Newton’s laws, he recognized that it could be explained by a ring of matter around the Sun. However, he may just have been acknowledging the latest hypothesis. In his review of astronomy and the new mechanics just two years later (quoted above) he made no mention of Seeliger’s hypothesis or a circumsolar ring as a possible explanation for the anomaly, and he clearly treated the anomaly as a fact that could be used to discriminate between theories of gravity. (Incidentally, it’s odd that Poincare was apparently familiar with the current astronomical literature regarding Seeliger’s hypothesis in 1906, and yet in 1908 he was still using for Mercury’s perihelion advance the figure 38”, which was Leverrier’s original value, but which had been raised to about 43” by Newcomb in 1882.)

Similarly, in a review of gravitation theories, Walter Ritz wrote in 1909

Astronomical observations carried out over many centuries have revealed some deviations between observation and calculation, which cannot be explained by Newton’s law up to now, and which a new theory will have to explain. Of these anomalies by far the largest is of the planet Mercury, whose ellipse precesses slowly, under the effect of the remaining planets; but the observed precession is larger by approximately 42 arc-seconds per century than the computed. The difference is small, but nevertheless unquestionable and unexplained.

Again this clearly indicates not only that the precession of Mercury’s orbit was considered anomalous, but that it was widely suspected that its resolution would come from a new theory of gravity. Of course, Einstein was very familiar with Ritz’s work, having engaged him in a public debate in 1909 on the subject of the advanced solutions of Maxwell’s equations.

In any case, we do have one definite piece of evidence for the fact that Einstein (like Poincare) regarded Mercury’s precession as anomalous, and as something to be explained by a new theory of gravity – even before Poincare’s 1908 book. In December 1907, just as Einstein was beginning to work seriously on his ideas about a relativistic theory of gravity (and just after having “the happiest thought of my life”, i.e., the equivalence principle), he wrote in a letter to his friend Conrad Habicht

At the moment I am working on a relativistic analysis of the law of gravitation by means of which I hope to explain the still unexplained secular changes in the perihelion of Mercury.

How had Einstein come to know, by 1907, of the precession of Mercury’s orbit? One possibility is that he read about it in Mach’s “The Science of Mechanics”, which he had studied in his student days (on Besso’s recommendation) and again in Bern with the “Olympia Academy”, and which is known to have played a significant role in his thinking as he worked to develop general relativity. Mach wrote that most physicists had concluded (with Laplace) that the speed of gravity must be much greater than that of light, and then he went on to say

Paul Gerber alone (“Ueber die raumliche u. zeitliche Ausbreitung der Gravitation,” Zeitschrift f. Math. u. Phys., 1898, II), from the perihelial motion of Mercury, forty-one seconds in a century, finds the velocity of propagation of gravitation to be the same as that of light. This would speak in favor of the ether as the medium of gravitation.

One could easily imagine that, in trying to reconcile gravitation with special relativity, Einstein might have gleaned from these words both the existence of the anomaly in Mercury’s precession and the exciting possibility that a theory in which gravity propagates at the speed of light might account for this precession. If he had read Mach’s book by 1907, this could account for his statement to Habicht. We also know that Einstein and Besso corresponded in 1916 about Gerber’s paper (i.e., a year before Gehrcke brought Gerber’s paper back to the attention of the physics community), in terms that suggest they had discussed it previously. When the anti-relativity league in 1920 charged Einstein with plagiarizing Gerber’s result, Einstein issued an angry statement, denying having had any knowledge of Gerber’s paper when he (Einstein) wrote his 1916 paper on general relativity, but he added that, even if he had known of it, there would have been no reason to mention it, because Gerber’s reasoning is rather incoherent, and his conclusion doesn’t follow from his premises.

Around 1913 Einstein and Besso actually worked out the perihelion advance implied by the so-called Entwurf theory of gravity that Einstein had developed with the help of Marcel Grossmann. They were disappointed to find that the theory predicted only 18 arc-seconds per century, less than half the observed amount. They decided not to publish the derivation.

Despite the failure to account for Mercury’s precession, Einstein was initially enthusiastic about the Entwurf theory, but gradually he began to lose confidence in it, and resumed the search for a satisfactory theory. Finally in November of 1915 Einstein arrived at the generally covariant field equations, which, to his delight, not only reduced to Newton’s theory in the first-order approximation, but gave in the second-order approximation the correct value for Mercury’s anomalous precession. In a letter to Sommerfeld on 28 November Einstein described how he had progressed from the Entwurf theory to general relativity:

In the last month I had one of the most stimulating, exhausting times of my life, and also one of the most successful…. For I realized that my existing gravitational field equations [the Entwurf theory of 1913] were entirely untenable! The following indications led to this:

1) I proved that the gravitational field on a uniformly rotating system does not satisfy the field equations.

2) The motion of Mercury’s perihelion came to 18” rather than 45” per century.

3) The covariance considerations in my paper of last year do not yield the Hamiltonian function H. When it is properly generalized, it permits an arbitrary H. From this it was demonstrated that covariance with respect to “adapted” coordinate systems was a flop.

Once every last bit of confidence in the result and the method of the earlier theories had given way, I saw clearly that it was only through a link with general covariance theory, i.e., with Riemann’s covariant, that a satisfactory solution could be found. Unfortunately, I have immortalized the final errors in this struggle in the Academy contributions… The final result is as follows: The gravitational field equations are generally covariant.

Thus, one of the three indications leading to his loss of confidence in the Entwurf theory was the failure of that theory to correctly account for the anomalous precession of Mercury’s orbit, and one of the main pieces of evidence he could cite in support of the generally covariant field equations was that they give the correct precession. Having said that, his reasons for believing he had finally arrived at the correct theory were mainly related to the logical coherence of it, and there really is very little arbitrariness in the correct derivation of the field equations from Einstein’s basic conceptual premises. The Entwurf theory and the other mis-steps along the way were just “immortalized errors”, and it was probably inevitable that sooner or later those errors would have been corrected, and the generally covariant field equations would be discovered. Indeed, Hilbert arrived at those same equations rather quickly once he began to work on the problem as Einstein had outlined it in a seminar at Gottingen the preceding summer. Nevertheless, the quantitative agreement with Mercury’s precession seems to have been psychologically very powerful for Einstein, and certainly contributed to his impression that the theory was correct. Pais says

This discovery was, I believe, by far the strongest emotional experience of Einstein’s scientific life, perhaps in all his life. Nature had spoken to him. He had to be right. ‘For a few days I was beside myself with joyous excitement’. Later he told Fokker that his discovery had given him palpitations of the heart. What he told de Haas is even more profoundly significant: when he saw that his calculations agreed with the unexplained astronomical observations, he had the feeling that something actually snapped in him…

In 1920 the publisher of an English edition of Einstein’s writings asked for a biographical sketch to be included in the book. Einstein replied with a brief summary of his life, beginning with his birth in Ulm in 1879 and ending with

1915. <Fundamental> Field equations of gravitation. Explanation of the perihelion motion of Mercury.

Returning to the 1907 letter to Habicht, Pais’ translation differs from the translations of Anna Beck (Einstein’s Collected Papers) and Roseveare. Pais translated the passage as

At this time I am [again] busy with considerations on relativity theory in connection with the law of gravitation… I hope to clear up the so-far unexplained secular changes of the perihelion length of Mercury… [but] so far it does not seem to work.

The concluding phrase (“so far it does not seem to work”) was not included in the English translation in the Collected Papers, but the documentary volume with the original German text includes a note explaining that Einstein appended this phrase at the foot of the page. Seelig in his 1956 biography rendered the phrase as “So far I have not managed to succeed”. (The original German was “bis jetzt scheint es aber nicht gelingen zu wollen”.) Various translators have also differed in their renderings of the changes in the perihelion length (Pais), the perihelion movement (Seelig), the perihelion motion (Roseveare), or simply the perihelion (Beck). (Einstein used the word “Perihellänge”.)

Incidentally, the popular book “The Evolution of Physics” (1938) by Einstein and Leopold Infeld says

The deviation of the motion of the planet Mercury from the ellipse was known before the general relativity theory was formulated, and no explanation could be found. On the other hand, general relativity developed without any attention to this special problem [my emphasis]. Only later was the conclusion about the rotation of the ellipse in the motion of a planet around the sun drawn from the new gravitational equations.

Considering that Einstein began his search for a new gravitational theory in 1907 with the expressed purpose (as stated in his letter to Habicht) of explaining the anomalous precession of Mercury, and that he kept this objective in view throughout the intermediate development (including the Entwurf of 1913), and considering that Einstein listed the failure of the Entwurf theory to give the correct perihelion of Mercury as one of the three reasons that led him to lose faith in that theory, which then led him to the fully covariant theory of general relativity, it seems hard to justify the claim that general relativity was developed without any attention to this problem. This claim is somewhat similar to Einstein’s assertions that special relativity was developed without any attention to the Michelson and Morley experiment – despite the fact that at other times (notably his 1922 talk in Japan on how he developed the theory of relativity) he seemed to acknowledge that this experiment had been an important factor in his thinking. In both cases it’s perfectly correct to say that the theories follow logically and almost without ambiguity from very broad and fundamental principles, so they were certainly not ad hoc explanations of the respective experimental facts. Nevertheless it is historically inaccurate to claim that general relativity was developed “without any attention” to Mercury’s anomalous precession.

We may be able to account for the clearly erroneous claim in “Evolution of Physics” by the fact that Einstein had very little to do with the actual writing of the book. He apparently agreed to lend his name to the project in order to help his friend Infeld financially after his one-year grant at the Institute for Advanced Study at Princeton expired. (The prospect of returning to Poland in 1938 was not very appealing.) It’s been said that Einstein’s actual contribution to the book was “negligible”, and Pais reports that Einstein was “not enthusiastic” about the book, and then concludes his brief discussion of it by quoting Einstein’s cryptic comment in reference to the project:

One should not undertake anything which endangers the tenuous bridge of confidence between people.

Return to Table of Contents