9.9 Locality and Temporal Asymmetry
|
|
|
|
No reasonable definition of reality could be expected to permit this. |
|
Einstein, Podolsky, and Rosen, 1935 |
|
|
|
We've seen that the concept of locality (along with the concept of causality) plays a crucial role in the EPR thesis and the interpretation of Bell's inequalities, but what precisely is the meaning of locality, especially in a quasi-metric spacetime in which the triangle inequality doesn't hold? The general idea of locality in physics is based on some concept of nearness or proximity, and the assertion that physical effects are transmitted only between suitably "nearby" events. From a relativistic standpoint, locality is often defined as the proposition that all causal effects of a particular event are restricted to the interior (or surface) of the future null cone of that event, which effectively prohibits communication between spacelike-separated events (i.e., no faster-than-light communication). However, this restriction clearly goes beyond a limitation based on proximity, because it distinguishes between the future null cone and the past null cone, thereby asserting a profound temporal asymmetry in the fundamental processes of nature. |
|
|
|
What is the basis of this asymmetry? It certainly is not apparent in the form of the Minkowski metric, nor in Maxwell's equations. In fact, as far as we know, all the fundamental processes of nature are perfectly time-symmetric, with the single exception of certain processes involving the decay of neutral kaons. However, even in that case, the original experimental evidence in 1964 for violation of temporal symmetry was actually a demonstration of asymmetry in parity and charge conjugacy, from which temporal asymmetry is indirectly inferred on the basis of the CPT Theorem. As recently as 1999 there were still active experimental efforts to demonstrate temporal asymmetry directly. In any case, aside from the single rather subtle peculiarity in the behavior of neutral kaons, no one has ever found any evidence at all of temporal asymmetry in any fundamental interaction. How, then, do we justify the explicit temporal asymmetry in our definition of locality for all physical interactions? |
|
|
|
As an example, consider electromagnetic interactions, and recall that the only invariant measure of proximity (nearness) in Minkowski spacetime is the absolute interval |
|
|
|
|
|
|
|
which is zero between the emission and absorption of a photon. Clearly, any claim that influence can flow from the emission event to the absorption event but not vice versa cannot be based on an absolute concept of physical nearness. Such a claim amounts to nothing more or less than an explicit assertion of temporal asymmetry for the most fundamental interactions, despite the complete lack of justification or evidence for such asymmetry in photon interactions. Einstein commented on the unnaturalness of irreversibility in fundamental interactions in a 1909 paper on electromagnetic radiation, in which he argued that the asymmetry of the elementary process of radiation according to the classical wave theory of light was inconsistent with what we know of other elementary processes. |
|
|
|
While in the kinetic theory of matter there exists an inverse process for every process in which only a few elementary particles take part (e.g., for every molecular collision), according to the wave theory this is not the case for elementary radiation processes. According to the prevailing theory, an oscillating ion produces an outwardly propagated spherical wave. The opposite process does not exist as an elementary process. It is true that the inwardly propagated spherical wave is mathematically possible, but its approximate realization requires an enormous number of emitting elementary structures. Thus, the elementary process of light radiation as such does not possess the character of reversibility. Here, I believe, our wave theory is off the mark. Concerning this point the Newtonian emission theory of light seems to contain more truth than does the wave theory, since according to the former the energy imparted at emission to a particle of light is not scattered throughout infinite space but remains available for an elementary process of absorption. |
|
|
|
In the same paper he wrote |
|
|
|
For the time being the most natural interpretation seems to me to be that the occurence of electromagnetic fields of light is associated with singular points just like the occurence of electrostatic fields according to the electron theory. It is not out of the question that in such a theory the entire energy of the electromagnetic field might be viewed as localized in these singularities, exactly like in the old theory of action at a distance. |
|
|
|
This is a remarkable statement coming from Einstein, considering his deep commitment to the ideas of locality and the continuum. The paper is also notable for containing his premonition about the future course of physics: |
|
|
|
Today we must regard the ether hypothesis as an obsolete standpoint. It is undeniable that there is an extensive group of facts concerning radiation that shows that light possesses certain fundamental properties that can be understood far more readily from the standpoint of Newton's emission theory of light than from the standpoint of the wave theory. It is therefore my opinion that the next stage in the development of theoretical physics will bring us a theory of light that can be understood as a kind of fusion of the wave and emission theories of light. |
|
|
|
Likewise in a brief 1911 paper on the light quantum hypothesis, Einstein presented reasons for believing that the propagation of light consists of a finite number of energy quanta which move without dividing, and can be absorbed and generated only as a whole. Subsequent developments (quantum electrodynamics) have incorporated these basic insights, leading us to regard a photon (i.e., an elementary interaction) as an indivisible whole, including the null-separated emission and absorption events on a symmetrical footing. This view is supported by the fact that once a photon is emitted, its quantum phase does not advance while "in flight", because quantum phase is proportional to the absolute spacetime interval, which, as discussed in Section 2.1, is what gives the absolute interval its physical significance. If we take seriously the spacetime interval as the absolute measure of proximity, then the transmission of a photon is, in some sense, a single event, coordinated mutually and symmetrically between the points of emission and absorption. |
|
|
|
This image of a photon as a single unified event with a coordinated emission and absorption seems unsatisfactory to many people, partly because it doesn't allow for the concept of a "free photon", i.e., a photon that was never emitted and is never absorbed. However, it's worth remembering that we have no direct experience of "free photons", nor of any "free particles", because ultimately all our experience is comprised of completed interactions. (Whether this extends to gravitational interactions is an open question.) Another possible objection to the symmetrical view of elementary interactions is that it doesn't allow for a photon to have wave properties, i.e., to have an evolving state while "in flight", but this objection is based on a misconception. From the standpoint of quantum electrodynamics, the wave properties of electromagnetic radiation are actually wave properties of the emitter. All the potential sources of a photon have a certain (complex) amplitude for photon emission, and this amplitude evolves in time as we progress along the emitter's worldline. However, as noted above, once a photon is emitted, its phase does not advance. In a sense, the ancients who conceived of sight as something like a blind man's incompressible cane, feeling distant objects, were correct, because our retinas actually are in "direct" contact, via null intervals, with the sources of light. The null interval plays the role of the incompressible cane, and the wavelike properties we "feel" are really the advancing quantum phases of the source. |
|
|
|
One might think that the reception amplitude for an individual photon must evolve as a function of its position, because if we had (contra-factually) encountered a particular photon one meter further away from its source than we did, we would surely have found it with a different phase. However, this again is based on a misconception, because the photon we would have received one meter further away (on the same timeslice) would necessarily have been emitted one light-meter earlier, carrying the corresponding phase of the emitter at that point on its worldline. When we consider different spatial locations relative to the emitter, we have to keep clearly in mind which points they correspond to along the worldline of the emitter. |
|
|
|
Taking another approach, it might seem that we could "look at" a single photon at different distances from the emitter (trying to show that its phase evolves in flight) by receding fast enough from the emitter so that the relevant emission event remains constant, but of course the only way to do this would be to recede at the speed of light (i.e., along a null interval), which isn't possible. This is just a variation of the young Einstein's thought experiment about how a "standing wave" of light would appear to someone riding along side it. The answer, of course, is that it’s not possible for a material object to move along-side a pulse of light (in vacuum), because light exists only as completed interactions on null intervals. If we attempted such an experiment, we would notice that, as our speed of recession from the source gets closer to c, the difference between the phases of the photons we receive becomes smaller (i.e., the "frequency" of the light gets red-shifted), and approaches zero, which is just what we should expect based on the fact that each photon is simply the lightlike null projection of the emitter's phase at a point on the emitter's worldline. Hence, if we stay on the same projection ray (null interval), we are necessarily looking at the same phase of the emitter, and this is true everywhere on that null ray. This leads to the view that the concept of a "free photon" is meaningless, and a photon is nothing but the communication of an emitter event's phase to some null-separated absorber event, and vice versa. |
|
|
|
More generally, since the Schrodinger wave function propagates at c, it follows that every fundamental quantum interaction can be regarded as propagating on null surfaces. Dirac gave an interesting general argument for this strong version of Huygens' Principle in the context of quantum mechanics. In his "Principles of Quantum Mechanics" he noted that a measurement of a component of the instantaneous velocity of a free electron must give the value ±c, which implies that electrons (and massive particles in general) always propagate along null intervals, i.e., on the local light cone. At first this may seem to contradict the fact that we observe massive objects to move at speeds much less than the speed of light, but Dirac points out that observed velocities are always average velocities over appreciable time intervals, whereas the equations of motion of the particle show that its velocity oscillates between +c and −c in such a way that the mean value agrees with the average value. He argues that this must be the case in any relativistic theory that incorporates the uncertainty principle, because in order to measure the velocity of a particle we must measure its position at two different times, and then divide the change in position by the elapsed time. To approximate as closely as possible to the instantaneous velocity, the time interval must go to zero, which implies that the position measurements must approach infinite precision. However, according to the uncertainty principle, the extreme precision of the position measurement implies an approach to infinite indeterminancy in the momentum, which means that almost all values of momentum - from zero to infinity - become equally probable. Hence the momentum is almost certainly infinite, which corresponds to a speed of ±c. This is obviously a very general argument, and applies to all massive particles (not just fermions). This oscillatory propagation on null cones is discussed further in Section 9.11. |
|
|
|
Another argument that seems to favor a temporally symmetric view of fundamental interactions comes from consideration of the exchange of virtual photons. (Whether virtual particles deserve to be called "real" particles is debatable; many people prefer to regard them only as sometimes useful mathematical artifacts, terms in the expansion of the quantum field, with no ontological status. On the other hand, it's possible to regard all fundamental particles that way, so in this respect virtual particles are not unique.) The emission and absorption points of virtual particles may be space-like separated, and we therefore can't say unambiguously that one happened "before" the other. The temporal order is dependent on the reference frame. Surely in these circumstances, when it's not even possible to say absolutely which side of the interaction was the emission and which was the absorption, those who maintain that fundamental interactions possess an inherent temporal asymmetry have a very difficult case to make. Over limited ranges, a similar argument applies to massive particles, since there is a non-negligible probability of a particle traversing a spacelike interval if it's absolute magnitude is less than about h2/(2πm)2, where h is Planck's constant and m is the mass of the particle. So, if virtual particle interactions are time-symmetric, why not all fundamental particle interactions? (Needless to say, time-symmetry of fundamental quantum interactions does not preclude asymmetry for macroscopic processes involving huge numbers of individual quantum interactions evolving from some, possibly very special, boundary conditions.) |
|
|
|
Experimentally, those who argue that the emission of a photon is conditioned by its absorption can point to the results from tests of Bell's inequalities, because the observed violations of those inequalities are exactly what the symmetrical model of interactions would lead us to expect. Nevertheless, the results of those experiments are rarely interpreted as lending support to the symmetrical model, apparently because temporal asymmetry is so deeply ingrained in peoples' intuitive conceptions of locality, despite the fact that there is very little (if any) direct evidence of temporal asymmetry in any fundamental laws or interactions. |
|
|
|
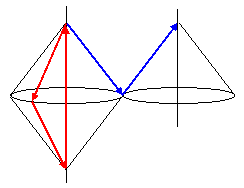
Despite the preceding arguments in favor of symmetrical (reversible) fundamental processes, there are clearly legitimate reasons for being suspicious of unrestricted temporal symmetry. If it were possible for general information to be transmitted efficiently along the past null cone of an event, this would seem to permit both causal loops and causal interactions with spacelike-separated events, as illustrated below. |
|
|
|
|
|
|
|
On such a basis, it might seem as if the Minkowskian spacetime manifold would be incapable of supporting any notion of locality at all. That triangle inequality fails in this manifold, so there are null paths connecting every two points, and this applies even to spacelike separated points if we allow the free flow of information in either direction along null surfaces. Indeed this seems to have been the main source of Einstein’s uneasiness with the “spooky” entanglements entailed by quantum theory. In a 1948 letter to Max Born, Einstein tried to clearly articulate his concern with entanglement, which he regarded as incompatible with “the confidence I have in the relativistic group as representing a heuristic limiting principle”. |
|
|
|
It is characteristic of physical objects [in the world of ideas] that they are thought of as arranged in a space-time continuum. An essential aspect of this arrangement of things in physics is that they lay claim, at a certain time, to an existence independent of one another, provided these objects ‘are situated in different parts of space’. Unless one makes this kind of assumption about the independence of the existence (the 'being-thus') of objects which are far apart from one another in space… the idea of the existence of (quasi) isolated systems, and thereby the postulation of laws which can be checked empirically in the accepted sense, would become impossible. |
|
|
|
In essence, he is arguing that without the assumption that it is possible to localize physical systems, consistent with the relativistic group, in such a way that they are causally isolated, we cannot hope to analyze events in any effective way, such that one thing can be checked against another. After describing how quantum mechanics leads unavoidably to entanglement of potentially distant objects, and therefore dispenses with the principle of locality (in Einstein’s view), he says |
|
|
|
When I consider the physical phenomena known to me, even those which are being so successfully encompased by quantum mechanics, I still cannot find any fact anywhere which would make it appear likely that the requirement [of localizability] will have to be abandoned. |
|
|
|
At this point the precise sense in which quantum mechanics entail non-classical “influences” (or rather, correlations) for space-like separated events had not yet been clearly formulated, and the debate between Born and Einstein suffered (on both sides) from this lack of clarity. Einstein seems to have intuited that quantum mechanics does indeed entail distant correlations that are inconsistent with very fundamental classical notions of causality and independence, but he was unable to formulate those correlations clearly. For his part, Born outlined a simple illustration of quantum correlations occuring in the passage of light rays through polarizing filters – which is exactly the kind of experiment that, twenty years later, provided an example of the very thing that Einstein said he had been unable to find, i.e., a fact which makes it appear that the requirement of localizability must be abandoned. It’s unclear to what extent Born grasped the non-classical implications of those phenomena, which isn’t surprising, since the Bell inequalities had not yet been formulated. Born simply pointed out that quantum mechanics allows for coherence, and said that “this does not go too much against the grain with me”. |
|
|
|
Born often argued that classical mechanics was just as probabilistic as quantum mechanics, although his focus was on chaotic behavior in classical physics, i.e., exponential sensitivity to initial conditions, rather than on entanglement. Born and Einstein often seemed to be talking past each other, since Born focused on the issue of determinism, whereas Einstein’s main concern was localizability. Remarkably, Born concluded his reply by saying |
|
|
|
I believe that even the days of the relativistic group, in the form you gave it, are numbered. |
|
|
|
One might have thought that experimental confirmation of quantum entanglement would have vindicated Born’s forecast, but we now understand that the distant correlations implied by quantum mechanics (and confirmed experimentally) are of a subtle kind that do not violate the “relativistic group”. This seems to be an outcome that neither Einstein nor Born anticipated; Born was right that the distant entanglement implicit in quantum mechanics would be proven correct, but Einstein was right that the relativistic group would emerge unscathed. But how is this possible? Considering that non-classical distant correlations have now been experimentally established with high confidence, thereby undermining the classical notion of localizability, how can we account for the continued ability of physicists to formulate and test physical laws? |
|
|
|
The failure of the triangle inequality (actually, the reversal of it) does not necessarily imply that the manifold is unable to support non-trivial structure. There are absolute distinctions between the sets of null paths connecting spacelike separated events and the sets of null paths connecting timelike separated events, and these differences might be exploited to yield a structure that conforms with the results of observation. There is no reason this cannot be a "locally realistic" theory, provided we understand that locality in a quasi-metric manifold is non-transitive. Realism is simply the premise that the results of our measurements and observations are determined by an objective world, and it's perfectly possible that the objective world might possess a non-transitive locality, commensurate with the non-transitive metrical aspects of Minkowski spacetime. Indeed, even before the advent of quantum mechanics and the tests of Bell's inequality, we should have learned from special relativity that locality is not transitive, and this should have led us to expect non-Euclidean connections and correlations between events, not just metrically, but topologically as well. From this point of view, many of the seeming paradoxes associated with quantum mechanics and locality are really just manifestations of the non-intuitive fact that the manifold we inhabit does not obey the triangle inequality (which is one of our most basic spatio-intuitions), and that elementary processes are temporally reversible. |
|
|
|
On the other hand, we should acknowledge that the Bell correlations can't be explained in a locally realistic way simply by invoking the quasi-metric structure of Minkowski spacetime, because if the timelike processes of nature were ontologically continuous it would not be possible to regard them as propagating on null surfaces. We also need our fundamental physical processes to consist of irreducible discrete interactions, as discussed in Section 9.10. |
|
|