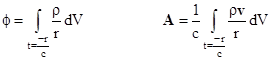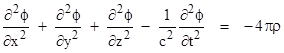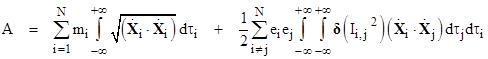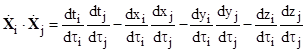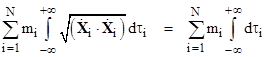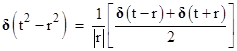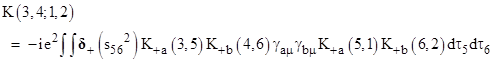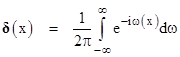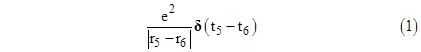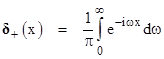9.10  Spacetime Mediation of Quantum Interactions

We were on the steamer from America to Japan, and I liked to take part in the social life on the steamer and, so, for instance, I took part in the dances in the evening. Paul, somehow, didn't like that too much but he would sit in a chair and look at the dances. Once I came back from a dance and took the chair beside him and he asked me, "Heisenberg, why do you dance?" I said, "Well, when there are nice girls, it is a pleasure to dance." He thought for a long time about it, and after about five minutes he said, "Heisenberg, how do you know beforehand that the girls are nice?"

                                                           W. Heisenberg

Most natural philosophers from Aristotle to Descartes held that material entities can influence each other only by coming into direct contact, i.e., “an object cannot act where it is not”. However, Newton’s theory of gravity undermined confidence in the doctrine of “direct contact”, because in Newton’s theory gravity is represented as an instantaneous universal force of attraction between every pair of objects, regardless of the distance between them, and regardless of whether the space between them contains any material substance. Admittedly Newton himself (in private writings) asserted that gravity must ultimately be attributable to some kind of process or condition in the intervening spaces between objects, but he was skeptical of any material mechanism for gravity.

During the century following the publication of Newton’s Principia the theory of gravitational force acting at a distance proved to be so successful that “force at a distance” became the standard model of physical interaction, and it was applied to the formulation of the laws of electricity and magnetism. Even after Oersted’s discovery of the link between these two forces, and the discovery of the dependence of these forces on the relative states of motion of the objects (rather than just their relative positions), Ampere was still able to formulate electrodynamics in terms of inverse-square forces at a distance, accounting for all the phenomena known at that time. The distant action interpretation of electrodynamics was carried on into the next century by Gauss, Weber, Lorenz, Lienard, Wiechert, and many others. However, at the same time, Faraday and Maxwell argued against the concept of distant action, and instead sought to represent electrodynamics in terms of direct local actions of an electromagnetic field – with mechanical properties – permeating all of space. One implication of this approach was that electromagnetic effects must require some time to propagate (through a succession of local actions) from place to place. This reinforced Maxwell’s belief in the necessity of an intervening medium, to embody the energy and momentum of action between emission and absorption. The detailed process of propagation (consistent with the known facts of electromagnetism) turned out to coincide with a model for the propagation of light. Hertz’s experimental verification of electromagnetic waves in 1887 was taken by many scientists as a conclusive demonstration of the field concept, and as a refutation of the distant action theories, which were then largely abandoned.

However, despite the success of the field interpretation, some scientists continued to work on developing the “distant action” approach. They noted that one of Maxwell’s original objections to the distant action theories – that any velocity-dependent force must violate conservation of energy – was unfounded, because the velocity-dependent potential of Weber is actually consistent with energy conservation – at least for velocities less than the speed of light. Also, the concepts of delayed propagation and “radiation” effects were not really as incompatible with distant-action theories as it might seem. Indeed in 1867 Ludwig Lorenz had proposed a distant action theory based on retarded potentials, formally identical to the Newtonian gravitational potential, but with a light-speed delay to account for the finite propagation speed, and this theory predicts all the same “radiation” effects as does Maxwell’s theory. The electromagnetic potentials affecting a charged particle at any given event are expressed as simple integrals of the charge density ρ and velocity v over the volume of the past light cone of the event, as follows

where r is the spatial distance from the event in question (with respect to any specified inertial coordinate system). The integrals are evaluated over the past light cone of the event, so the charge density and velocity appearing in these integrands are functions of position and time ρ(r, –r/c) and v(r, –r/c), with the understanding that we have set t = r = 0 at the event in question. It’s notable that, in this formulation, the effects of electromagnetic “radiation” are actually just direct (albeit distant and retarded) actions between charged particles. Also, notice that the potential at a given particle depends only on the retarded positions of other particles, so there is no “self-energy”, a troublesome concept for field theories. Despite the elegance of this “distant action” formulation, and the fact that it accounts for all the same phenomena as Maxwell’s field theory, this approach continued to be regarded as of secondary importance, largely because the precepts of contiguous local action and local conservation of energy and momentum seem more compatible with field theories than with distant action theories.

Nevertheless, one feature of the retarded potential formulation prompted a re-consideration of a very fundamental issue, namely, the temporal symmetry of the basic equations governing electromagnetism versus the apparent asymmetry of phenomena such as radiation. It can be shown that the scalar potential satisfies the equation

and this is equally well solved by either of the two functions

where ϕ₁ is called the retarded potential and ϕ₂ the advanced potential. The usual presumption was that only the retarded potential was physically relevant, but the justification for excluding the advanced potential was unclear. In 1902 Karl Schwarzschild proposed a fully time-symmetrical formulation of electrodynamics, essentially making use of both the advanced and retarded potentials. It attracted little attention at the time, but the same formulation was later (independently) developed by Fokker and Tetrode in 1922. Expressed in modern notation, they asserted that the trajectories of a set of N particles with masses m_j and charges e_j are such as the make stationary a certain action quantity A, so the law of motion is δA = 0 where

with

and

We use the bold δ for the Dirac delta function to distinguish it from the variational symbol δ. As noted above, an action equivalent to this was originally formulated by Schwarzschild prior to the development of special relativity, and yet it invokes what we would today call the invariant spacetime I_i,j between two particles. At the time, scientists still believed in the absolute significance of spatial and temporal intervals, so this formulation could only seem even further removed from the requirement of “local contact”, because it entailed a force between particles separated not only in space but also in time. For this reason, the “action at a distance” formulation was unappealing. However, the situation appears quite different in the context of Minkowski spacetime. The spacetime interval is the only physically invariant measure of the “distance” between two particles. The appearance of the delta function of the squared spacetime interval in the Schwarzschild action implies that the influence between two particles propagates entirely along null intervals. Therefore, one can argue that “action at a distance” is a misnomer when applied to this theory, because the propagation of action is restricted to null spacetime distances. In this way, special relativity reconciles the two seemingly contradictory historical traditions of Descartes and Newton, i.e., of direct contact and action at a distance.

Notice that the first term of A reduces to

so the variational principle for a single particle gives the classical law of inertia

It’s also worth noting that the summation in the second term of A excludes i = j, which is to say, a particle does not act on itself. This was considered to be one of the appealing features of this approach, because it avoids the troublesome infinite self-energy entailed by field theories (for discrete point-like charges). On the other hand, one might imagine that the first term in A represents the i = j case that is “missing” from the second term. In fact it is possible (with certain provisos) to modify the expression for A in such a way that the first term is eliminated and the summation in the second term include the self-action term i = j, signifying that the inertia of a charged particle is due to electromagnetic self-action. However, this can only be done at the expense of strict relativistic invariance, so it is not entirely satisfactory, and of course it does not account for quantum effects.

Another noteworthy feature of the Schwarzschild action is that it is temporally symmetrical, making equal use of both the advanced and retarded potentials, which is to say, the interactions are conveyed along all the null intervals between the worldlines of two particles, on both the forward and past lightcones of each event on those worldlines. This can be seen explicitly from the following identity

which also shows how the action A is related to the usual Coulomb potential e²/r between two particles of charge e at a distance r. Thus the Schwarzschild action also offers a resolution of the debate about temporal symmetry and the physical significance of advanced potentials. The symmetry of interactions according to this formulation of electromagnetism was stressed by Hugo Tetrode, who commented evocatively in 1922 on the implications of this interpretation:

The sun would not radiate if it were alone in space and no other bodies could absorb its radiation… If for example I observed in my telescope yesterday evening that star which let us say is 100 light years away… the star or individual atoms of it knew already 100 years ago that I, who then did not even exist, would view it yesterday evening at such and such a time.

He argued that quantum electrodynamics should be describable entirely in terms of interactions “at a distance” along the null intervals between light-like separated material particles. In a letter to Ehrenfest in 1922 Einstein wrote enthusiastically

There is a very intelligent paper by Tetrode in Zeitschrift fur Physik about the quantum problem. Maybe he’s right; either way, by this paper he demonstrates that he is a first-ranking mind. Nothing has been as fundamentally gripping for me in a long time. We, incidentally, also once discussed the possible importance of the relativistic distance 0 (?) in solving the quantum problems…”

Subsequently the same approach to classical electromagnetism was developed by Feynman and Wheeler in the 1940s. To account for the apparently asymmetric “radiation reaction” experienced by an accelerating charge (i.e., in terms of a field theory, the reaction on a charged particle to the radiation it emits when it is accelerated) without assuming that a particle acts on itself, they proposed that every ray along all the future light cone of a given particle eventually terminates at some other particle in the far distant future. Consequently, every acceleration of the given particle corresponds to slight accelerations of all those distant particles in the ideal future absorber, and the given particle is at the intersection of the past light cones of all those distant particles, and hence is subject to a reaction, which can be shown to exactly “mimic” the radiation reaction force of the conventional field theory with purely retarded waves. In essence the asymmetry is attributed to asymmetric boundary conditions by postulating complete absorption in the future. Whether or not this postulate is consistent with observation is questionable, and it has also been challenged on other grounds, but it does at least illustrate how phenomena that might seem to require a field theory may actually be modeled in terms of a direct action theory. Feynman once commented on these alternative points of view:

In the customary view, things are discussed as a function of time in very great detail. For example, you have the field at this moment, a differential equation gives you the field at the next moment and so on – a method which I shall call the Hamilton method, i.e., the time differential method. On the other hand, we have [in the expression for A] a thing that describes the character of the path throughout all of space and time. The behavior of nature is determined by saying her whole spacetime path has a certain character. For an action like A, the equations obtained by variation of the X(τ) functions are no longer at all easy to get back into Hamiltonian form. If you wish to use as variables only the coordinates of particles, then you can talk about the property of the paths - but the path of one particle at a given time is affected by the path of another at a different time. If you try to describe, therefore, things differentially… you need a lot of bookkeeping variables to keep track of what the particle did in the past. These are called field variables…. From the overall space-time view of the least action principle, the field disappears as nothing but bookkeeping variables insisted on by the Hamiltonian method.

Of course, by the time Feynman worked on this subject, it was known that classical physics was inadequate to account for all the phenomena, so the real objective in studying classical electrodynamics was to find a secure basis for extrapolating a viable quantum theory. The original theory of quantum mechanics replaced the classical concept of a discrete particle possessing a definite continuous path through space and time with a quantum field representing the amplitude of the probability that the particle would be found in any given region of state space. The early simplified version of quantum mechanics was not relativistically invariant, but a relativistic theory could be achieved by essentially repeating the quantization at a higher level, effectively quantizing the quantum field of the particle. Thus quantum field theory originated in efforts to reconcile quantum mechanics with special relativity. The first quantization gave a description of a particle in terms of a field representing the probabilities of all possible configurations of the particle, whereas the so-called “second quantization” described a meta-field representing the probabilities of all possible first-order fields of particles. According to one interpretation, different particles come in and out of existence, provided only that all conservation requirements are met. This “second quantization” was described by Pais as “the end of the game of marbles”, because it was no longer possible to represent events purely in terms of a fixed set of permanent particles. The Dirac equation, discussed in Section 9.4, was the first relativistically invariant description of a quantum particle – or rather, of the wave function of a particle – and it led immediately to the realization that anti-particles must also exist, and that particles can be created and annihilated. This might seem to render obsolete the particle as a suitable elementary entity, but Wheeler and Feynman proposed the ingenious idea that anti-particles are ordinary particles moving backwards in time. This seemed at least as plausible as Dirac’s hole theory, with its infinite sea of negative-energy electrons, and it allowed Feynman to pursue his particle-based approach.

Making use of many of the ideas he had explored in his re-formulation of classical electrodynamics as a direct action theory, Feynman went on to develop what he called the spacetime view of quantum field theory. Dirac had previously described how a probability amplitude could be associated with the entire path of a particle, rather than with just the particle at one specific time and place. The step analogous to “second quantization” was to consider that the overall probability amplitude for a particle to propagate from one given event in spacetime to another is simply the “sum over histories”, i.e., the integral of the probability amplitudes over all possible paths between those two events. This is called the path integral approach. For example, consider two electrons, denoted by a and b, initially at locations 1 and 2 respectively, and let K(3,4;1,2) denote the probability amplitude for these electrons to arrive at locations 2 and 4 respectively, taking into account the possibility of an exchange of one quantum of action (i.e., a photon, representing the first-order Coulomb interaction) between them, emitted and absorbed at the intermediate locations 5 and 6 along their respective paths. By reasoning very similar to that used in the Schwarzschild formulation of classical electrodynamics, Feynman developed the expression

where e is the elementary charge, g_am and g_bm are the Dirac matrices (see Section 9.4) representing the two electrons, and s₅₆² is the squared magnitude of the spacetime interval between events 5 and 6. Just as in the Schwarzschild action for classical electrodynamics, we see that the action propagates along null intervals, as indicated by the delta function. However, the “+” subscript on the delta function signifies that Feynman is taking only the “positive frequency” part of the delta function. Recall that the delta function can be expressed (somewhat loosely) as

Strictly speaking, this integral diverges, so this is not a well-defined expression, but if we cut off the integration at large but finite limits, we do get a function that converges on the delta function as the limits increase. The integral is taken over all frequencies w, positive and negative, but Feynman argued that we must restrict ourselves to just the positive frequencies, which amounts to assuming that a photon is emitted only into the forward light cone of a particle, and absorbed only from the past light cone – thereby sacrificing the perfect temporal symmetry of the classical Schwarzschild action. In summary, Feynman’s objective was to derive an expression for the amplitude of a particular interaction between two charged particles, corresponding to the Coulomb potential e²/r where e is the electric charge on each particle and r is the distance between the particles. In his notation, the interaction is “turned on” when one particle is at a time and place denoted by event 5, and the other is at the time and place denoted by event 6. He begins with a double integral over the path parameters dτ₅ and dτ₆ , and to accept contributions only when t₅ = t₆ he multiplies the integrand by the delta function δ(t₅ – t₆), treating the Coulomb interaction non-relativistically as if it acted instantaneously. Thus his expression included a factor of the form

But then he notes that, relativistically, the interaction is not instantaneous, but is retarded by the light-speed delay in propagating from one particle to the other. Thus, if we define the symbols t₅₆ = t₅ – t₆ and r₅₆ = r₅ – r₆, Feynman proposes to modify the formula, substituting in place of δ(t₅₆) the delta function δ(t₅₆ – r₅₆), which signifies that the integral will accept contributions when the particle at 5 is on the forward light cone of the particle at 6. (Note that we are using units such that the speed of light has the value 1.) But now he says “this turns out to be not quite right, for when this interaction is represented by photons, they must be of only positive energy, while the Fourier transform of δ(t₅₆ – r₅₆) contains frequencies of both signs”. He is referring to the Fourier representation of the delta function noted above, in which the integral extends over values of the frequency parameter w from negative to positive infinity. (Oddly enough, he doesn’t mention that this representation doesn’t actually converge.) To remedy this, he defines a new type of delta function, denoted by δ₊(x), consisting of only the positive frequency parts of the usual delta function, i.e.,

Here the integral ranges from 0 to positive infinite, and we have multiplied by 2 to normalize the result so that the integral of δ₊(x) over all x is 1. This is conceptually very significant, since it effectively imposes temporal asymmetry on the interaction occurring on this null interval. With this step, Feynman relinquished the time-symmetry that had attracted him to the direct action interpretation in the first place.

The previous expression represented the interaction for the null interval when (in Feynman’s nomenclature) the particle at 5 is on the forward light cone of the particle at 6, i.e., when t₅₆ – r₅₆ vanishes. To account for the interaction when the particle at 6 is on the forward light cone of the particle at 5, Feynman says we need to include a term representing the condition when t₅₆ + r₅₆ vanishes. (This is not to be confused with an attempt to account for temporally symmetrical interaction between the two particles along any single null interval.) Specifically, he says we need to average the two possibilities, so he replaces δ(t₅ – t₆) in equation (1) with the average of δ₊(t₅₆ – r₅₆) and δ₊(t₅₆ + r₅₆), which we’ve seen is δ₊(t₅₆² – r₅₆²). Thus we arrive at a relativistically invariant factor.

Even this, however, turned out to be “not quite right” if we are to avoid infinities in the calculations, so Feynman proposed to replace the delta function with a function that is not perfectly sharp, so that most, but not all, of the contribution occurs when the argument is zero. He found that the results were insensitive to the precise value of the cutoff. (This corresponds to the fact that the Fourier representation of the delta function does not converge, but it can be approximated with arbitrary precision by specifying an arbitrarily large cutoff frequency.)

It’s interesting that all of classical mechanics and electrodynamics can be expressed by the simple action A described above, but this formulation does not include gravity. Considering the formal similarities between the electric force and the gravitational force, one might expect that gravitation would be most naturally incorporated into A by adding an interactive term similar to the summation representing electromagnetic interactions, with the gravitational “charge” m in place of the electric charge e. However, the masses of the particles already appear in the first term in A, which we’ve seen corresponds to the inertial behavior of objects, i.e., δ∫dτ = 0. This variational formula originally pre-supposed a fixed Minkowskian background metric, but in general relativity the spacetime metric is allowed to deviate from flatness (in accord with the field equations in the presence of mass-energy), and with this allowance the very same variational equation entails all the effects of the gravitational interactions between objects.

Ironically, prior to general relativity, many efforts had been made to absorb the first term of A into the second, representing inertia as a aspect of electromagnetism, whereas Einstein’s general relativity emerged from his focus on interpreting gravitation as an aspect of inertia, separate and distinct from electromagnetism. Of course, the variational expression for the path of a particle represents only the passive response, whereas the entire gravitational interaction must explain how the particle actively affects the metric. The conventional bifurcation of phenomena into separate active and passive aspects seems to work surprisingly well, even though it is difficult to rigorously justify. This dubious aspect of the conventional treatment is mentioned even in traditional texts such as Jackson’s “Classical Electrodynamics”, albeit not until the final chapter.

…the problems of electrodynamics have been divided into two classes: one in which the sources of charge and current are specified and the resulting electromagnetic fields are calculated, and the other in which the external electromagnetic fields are specified and the motions of charged particles or currents are calculated… this manner of handling problems in electrodynamics can be of only approximate validity… A correct treatment must include the reaction of the radiation on the motion of the sources... [but] a completely satisfactory classical treatment of the reactive effects of radiation does not exist. The difficulties presented by this problem touch one of the most fundamental aspects of physics, the nature of an elementary particle… the basic problem remains unsolved.

If we take the view that radiation effects on a given charged particle are actually just interactions (along null intervals) with other charged particles, we might say the difficulties presented by radiation reaction touch not only on the nature of elementary particles, but also on the inadequacy of attempts to represent local physical phenomena in isolation from all the other entities in the universe. In this sense, the "advantage" that is often claimed for the field interpretation in macroscopic applications – i.e., that it (seemingly) enables us to base our treatments on the state of matter and fields within a limited region – may actually be misleading.

Just as, in classical Maxwellian electrodynamics, the fields determine the motions of charges in spacetime while the charges determine the fields in spacetime, according to general relativity the shape of spacetime determines the motions of objects while those objects determine (or at least influence) the shape of spacetime. This dualistic structure naturally arises when we replace action-at-a-distance with purely local influences in such a way that the interactions between "separate" objects are mediated by an entity extending between them. We must then determine the dynamical attributes of this mediating entity, e.g., the electromagnetic field in electrodynamics, or spacetime itself in general relativity. Unfortunately, this inevitably introduces deep ambiguities, because, as Einstein wrote to Walter Dallenbach in 1917

…if the molecular interpretation of matter is correct, that is, if a portion of the world is to be represented as a finite number of moving points, then the continuum in modern theory contains much too multifarious possibilities. I also believe that this multifariousness is to blame for the foundering of our tools of description on quantum theory. The question seems to me to be how one can formulate statements about a discontinuum without resorting to a continuum (space-time); the latter would have to be banished from the theory as an extra construction that is not justified by the essence of the problem and that corresponds to nothing “real”. But for this we unfortunately are still lacking the mathematical form.

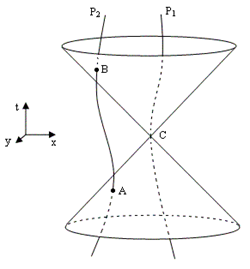
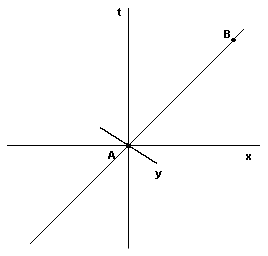
The basic problem is that, as Einstein put it, “the continuum is more comprehensive than the objects to be described”. This is the fundamental issue that has led to repeated attempts to dispense with the field-theoretic continuum approach and to describe phenomena purely in terms of direct interactions between some putative set of “tangible” entities. For a relativistic theory that respects ordinary notions of causality, the difficulties involved in such attempts are formidable. Consider the figure below, depicting the worldlines P₁ and P₂ of two charged particles. (Note that the particles can, in principle, be moved around by electrically neutral pliers, so their worldlines can be arbitrary timelike paths.)

According to the usual interpretation of classical electrodynamics the electric and magnetic potentials to which particle P₁ is subjected at the origin C (excluding those due to its own charge) are fully determined by the position and velocity of the particle P₂ at event A on the past light-cone of C. Of course, due to the temporal symmetry of Maxwell’s equations, we could just as well reverse the sign of t, meaning that the potentials at C would be determined by the position and velocity of P₂ at event B on the future light-cone of C (assuming there are no other charged particles of any significance). It might seem as if this would imply that the potential fields given by these two conditions must be equal, i.e., that q/r_A = q/r_B and hence r_A = r_B. However, this need not be the case, because the absolute values of the potential are unobservable; only the partial derivatives of the potential are significant. Furthermore, the electromagnetic potentials are inherently under-specified in the sense that they possess a gauge symmetry, as can be seen from the fact that the electric and magnetic fields are unchanged if we replace ϕ and A with

where Ω is a completely arbitrary scalar field. We are free to choose this function such that

but even this does not uniquely fix the potentials, because the electric and magnetic fields are also unchanged if we augment Ω by any arbitrary scalar field whose d’Alembertian vanishes. Thus there are many different potential fields that yield any given electric and magnetic fields, so it isn’t too implausible that the electric and magnetic fields at any given instant are consistent with both the advanced and the retarded potential fields. This is somewhat analogous to the Laplacian determinism of classical mechanics, according to which the state of the universe at any given time can equally well be inferred from a complete specification of the conditions in the future as from a specification of conditions in the past. There is, however, an extra complication in electrodynamics due to the light cone structure. In order to determine the future and past states based on the state at a given instant, it is necessary to specify not only the positions and velocities of all the particles, but also the values of the electric and magnetic fields at every point. If we wished to specify only the positions and velocities of the particles, it would be necessary to specify them not just at a given instant but for all time into the past (or into the future), assuming an infinitely large universe.

In 1909 Walter Ritz and Albert Einstein (former classmates at the University of Zurich) debated the question of whether there is a fundamental temporal asymmetry in electrodynamics, and if so, whether Maxwell’s equations (as they stand) can justify this asymmetry. As mentioned above, the potential field equation is equally well solved by either the retarded potential ϕ₁ or the advanced potential ϕ₂. Ritz believed the exclusion of the advanced potentials represents a physically significant restriction on the set of possible phenomena, and yet this restrictions has no justification in the context of Maxwell’s equations. From this he concluded that Maxwell’s equations were fundamentally flawed, and could not serve as the basis for a valid theory of electrodynamics. Ironically, Einstein too did not believe in Maxwell’s equations, at least not when it came to the microstructure of electromagnetic radiation, as he had written in his 1905 paper on what later came to be called photons. However, Einstein was not troubled by the exclusion of the advanced potentials. He countered Ritz’s argument by pointing out (in his 1909 paper “On the Present State of the Radiation Problem”) that the range of solutions to the field equations is not reduced by restricting ourselves to the retarded potentials, because all the same overall force-interactions can be represented equally well in terms of advanced or retarded potentials (or some combinations of both). He wrote

If ϕ₁ and ϕ₂ are [retarded and advanced] solutions of the [potential field] equation, then ϕ₃ = a₁ϕ₁ + a₂ϕ₂ is also a solution if a₁ + a₂ = 1. But it is not true that the solution ϕ₃ is a more general solution than ϕ₁ and that one specializes the theory by putting a₁ = 1, a₂ = 0. Putting ϕ = ϕ₁ amounts to calculating the electromagnetic effect at the point x,y,z from those motions and configurations of the electric quantities that took place prior to the instant t. Putting ϕ = ϕ₂ we are determining the above electromagnetic effects from the motions that take place after the instant t. In the first case the electric field is calculated from the totality of the processes producing it, and in the second case from the totality of the processes absorbing it. If the whole process occurs in a (finite) space bounded on all sides, then it can be represented in the form ϕ = ϕ₁ as well as in the form ϕ = ϕ₂. If we consider a field that is emitted from the finite into the infinite, we can naturally use only the form ϕ = ϕ₁, precisely because the totality of the absorbing processes is not taken into consideration. But here we are dealing with a misleading paradox of the infinite. Both kinds of representations can always be used, regardless of how distant the absorbing bodies are imagined to be. Thus one cannot conclude that the solution ϕ = ϕ₁ is more special than the solution ϕ = a₁ϕ₁ + a₂ϕ₂ where a₁ + a₂ = 1.

Ritz objected to this, pointing out that there is a real observable asymmetry in the propagation of electromagnetic waves, because such waves invariably originate in small regions and expand into larger regions as time increases, whereas we never observe the opposite happening. Einstein replied that a spherical wave-shell converging on a point is possible in principle, it is just extremely improbable that a widely separate set of boundary conditions would be sufficiently coordinated to produce a coherent in-going wave. Essentially the problem is pushed back to one of asymmetric boundary conditions. On the other hand, as discussed in Section 9.9, later in the same year Einstein acknowledged that, from the standpoint of quantum theory, an inward propagating wave does not exist as an elementary process, and this suggests that the classical wave theory of radiation is off the mark.

Ritz died in July of 1909 at the age of 31, just six weeks after the last published exchange with Einstein appeared. Interestingly, 30 years later, Richard Feynman as a young graduate student gave his first formal talk at a seminar at Princeton describing his theory of classical electromagnetism based on direct interaction, using half advanced and half retarded potentials. Feynman’s autobiographical book (“Surely You’re Joking Mr. Feynman”) includes a chapter entitled “Monster Minds”, in which he recalls his alarm upon learning, shortly before the talk, that the attendees would include Henry Norris Russell, John von Neumann, Wolfgang Pauli and Albert Einstein. Just as the talk was about to get started, Feynman was writing some equations on the blackboard, and Einstein walked in and said “Hello, I’m coming to your seminar, but first, where is the tea?” At this time, Feynman wasn’t aware of Einstein’s debate with Ritz back in 1909 on the subject to advanced and retarded potentials. It’s interesting that some of the ideas of Feynman’s talk that day, such as the need for a complete absorber in the future, were already familiar to Einstein. After the talk was over, Pauli raised some objection to the theory, and asked if Einstein agreed. “No”, Einstein replied, “I find only that it would be very difficult to make a corresponding theory for gravitational interaction”.

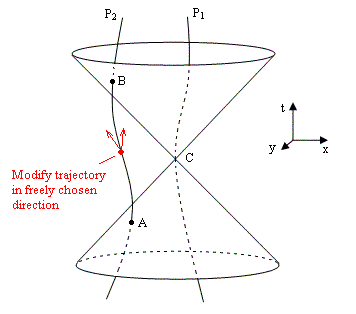
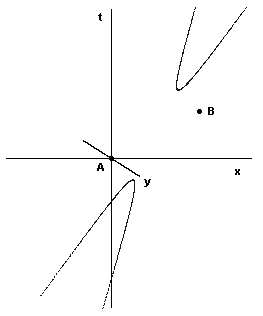
As we’ve seen, back in 1909 Einstein had answered Ritz by asserting that the electromagnetic field at a given point can be calculated equally well from either the totality of the processes producing it or the totality of the processes absorbing it. This would certainly follow if all processes were symmetrical under time reversal, as are Maxwell’s equations of the electromagnetic field. However, as noted in Section 5.6, Einstein himself later remarked that “Maxwell’s theory of the electric field remained a torso, because it was unable to set up laws for the behavior of electric density, without which there can, of course, be no such thing as an electromagnetic field”. A first step toward completing Maxwell’s theory was provided by the Lorentz force law F = q(E + v x B), describing how electric charges move in an electromagnetic field, but this equation is satisfactory only for sufficiently small accelerations, because it neglects the effects of a particle’s own field on itself. Attempts to create a fully satisfactory theory of classical electrodynamics, valid for arbitrary motions, seem to inevitably lead to conflicts with the principle of causality. For example, the Lorentz-Dirac equation, developed by Dirac in 1938, leads to the conclusion that if an electric charge is subjected to a force, it must begin to accelerate just prior to the application of the force. This conflict with the usual ideas of causality was already implicit in Einstein’s answer to Ritz, as can be seen in the figure below.

Recall that the field to which the particle at C is subjected can be calculated (according the equations for the retarded potentials) from the positions of the charges, such as A, on the past light cone of C. But the field at C can also be computed from the positions of the charges, such as B, on the future light cone of C. In Einstein’s terminology, the field at C is produced by A and absorbed by B. But suppose that, after the particle moving along the worldline P₂ has passed through event A, but before it passes through event B, we subject it to a force that changes its trajectory, so it doesn’t pass through B. Thus it seems we can set up a conflict of causality. Of course, it’s unrealistic to consider a universe with just two electrically charged particles. In more realistic models the field at C would be absorbed by more than just the charge at B. Nevertheless, if we postulate that the charge configuration in the future can be freely established by the exercise of free will, independent of the charge distribution of the past, we encounter the same conflict with causality, so it isn’t surprising that a classical theory of electrodynamics of arbitrarily moving charges leads to acausal results. Just as in the case of Bell’s inequality and quantum entanglement, the difficulty arises from the presumption of free will, i.e., the presumption that new information is injected into the world, not a consequence and indeed uncorrelated with the rest of the world.

In addition to these difficulties with causality, many of our common notions regarding the nature and extension of a posited mediating continuum are also called into question by the apparently "non-local" correlations in quantum mechanics, as highlighted by EPR experiments (see Section 9.5). The apparent non-locality of these phenomena arises from the fact that although we regard spacetime as metrically Minkowskian, we continue to regard it as topologically Euclidean. As discussed in the preceding sections, the observed phenomena are (at least arguably) more consistent with a completely Minkowskian spacetime, in which our concept of physical locality is the one directly induced by the pseudo-metric of spacetime. According to this view, the “path integral” concept advocated by Feynman might be expressed by saying that a quantum interaction originates on (or is "mediated" by) the locus of spacetime points that are null-separated from each of the interacting sites. The reduction of spacetime to nothing but the null intervals is one possible way of reducing the excessive “multifariousness” of the spacetime continuum. We saw above how delicate a proposition this is when, to avoid infinities, Feynman had to replace the delta function (representing a strict limitation to the null intervals) with a slightly less “sharp” function, which, however, could then be evaluated in the limit as it approached the delta function.

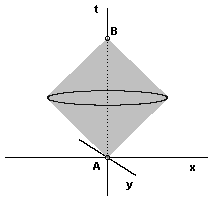
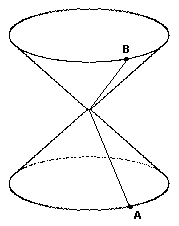
In general the locus of events that are null-separated from each of two given events is a quadratic surface in spacetime. For two timelike-separated events A and B the mediating locus is a closed surface as illustrated below (with one of the spatial dimensions suppressed).

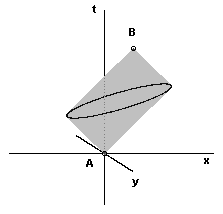
The mediating surface is shown here as a circle, but in four-dimensional spacetime it's actually a closed surface, spherical and purely spacelike relative to the frame in which the interval AB is stationary. We might imagine that this type of interaction corresponds to the temporal progression of massive real particles, with the surface area of the null locus being inversely proportional to the mass of the particle. Of course, relative to a frame in which A and B are in different spatial locations, the locus of intersection has both timelike and spacelike extent, and is an ellipse (or rather an ellipsoidal surface in four dimensions) as illustrated below.

The surface is purely spacelike and isotropic only when evaluated relative to its rest frame (i.e., the frame of the interval AB), whereas this surface maps to a spatial ellipsoid, consisting of points that are no longer simultaneous, relative to any other co-moving frame. The directionally asymmetric aspects of the surface area correspond precisely to the “transverse and longitudinal mass” components of the corresponding particles as a function of the relative velocity of the frames.

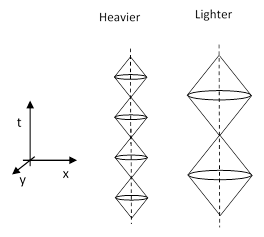
The propagation of a free massive particle along a timelike path through spacetime might be regarded (crudely) as involving a series of such surfaces, from which emanate inward-going "waves" along the nullcones in both the forward and backward direction, deducting the particle from the past focal point and adding it to the future focal point, as shown below for particles with different masses.

Recall that the frequency ν of the de Broglie matter wave of a particle of mass m is

where p_x, p_y, p_z are the components of momentum in the three directions. For a (relatively) stationary particle the momentum vanishes and the frequency is just ν = (mc²)/h sec^–1. Hence the time per cycle is inversely proportional to the mass. Since each cycle consists of an advanced and a retarded cone, the surface of intersection is a sphere (for a stationary mass particle) of radius r = h/mc, because this is how far along the null cones the wave propagates during one cycle. Now, h/mc is just the Compton scattering wavelength of a particle of mass m, which characterizes the spatial expanse over which a particle tends to "scatter" incident photons in a characteristic way. This can be regarded as the effective size of a particle.

A completely free massless particle – if such a thing existed – might just be represented by a monochromatic plane wave, but a real photon is necessarily emitted and absorbed as a directed quantum of action, so it corresponds to a bounded null interval in spacetime. (Note that the quantum phase of a photon does not advance while in transit between its emission and absorption, unlike massive particles. The oscillatory nature of electromagnetic waves arises from the advancing phase of the source, rather than from any phase activity of a photon “in flight”.) Thus the field excitation corresponding to a massless particle propagates at the speed of light and has no rest frame. In contrast, a massive particle has a rest frame, following a time-like path through spacetime. Nevertheless, we recall Dirac’s general argument (from the uncertainty principle) that all energy must propagate at essentially the speed of light if examined on the smallest scale. We account for the existence of time-like massive objects by the action of various binding effects, that contain energy in stable time-like configurations. At the level of the most elementary massive particles, such as quarks and electrons, this is believed to be accomplished by interactions with the so-called Higgs field. Roughly speaking, the distinct components of the particle field as described by the Dirac equation (see Section 9.4) could be regarded as individually massless, but they are woven together by their interaction with the ubiquitous Higgs field, resulting in a massive particle. This is somewhat analogous to the alternating inward and outward fluctuations in the figure above.

As a historical aside, it’s interesting to recall how during the early 1900’s many physicists were ready to conclude that all mass was electromagnetic in origin, i.e., attributable to self-induction with the electromagnetic field, based on Kaufmann’s results with accelerating ions, only to have their understanding of those results completely over-turned by special relativity. Subsequently quantum mechanics prompted yet another revision in the understanding of electrodynamics, and was originally thought to imply that spacetime descriptions are fundamentally inadequate for representing the phenomena. According to Bohr and Heisenberg (in the late 1920s), classical theory had consisted of causal relationships of phenomena described in terms of space and time, whereas the causal relationships of quantum theory cannot be applied to conventional descriptions of phenomena in terms of space-time. They contended that the evolution of a state vector according to the Schrodinger equation describes not a single set of trajectories of the constituent entities in spacetime, but rather a superposition of all possible trajectories. Nevertheless, they also held that this unitary evolution in Hilbert space (in modern terms) was not the whole story, because, as Bohr later wrote, “however far the phenomena transcend the scope of classical physical explanation, the account of all evidence must be expressed in classical terms”, by which he meant that descriptions of observations are expressed in terms of space and time. But this reduction to classical terms entails the notorious “jumps” in the state vector, which Bohr and Heisenberg saw as “the limitations placed on all space-time descriptions by the uncertainty principle”. Thus the dichotomy (or complementarity, as Bohr called it) was between the unitary evolution of the wave function on the one hand, and the reduction of observations to classical space-time descriptions on the other.

The Cophenhagen view of quantum mechanics evolved somewhat in later years, partly in response to criticisms from Einstein, who pointed out that the reduction to observation could not be merely descriptive, because the choice of measurements on one part of a system has implications for the results on other parts of the system. Ironically, Feynman later referred to his work on quantum electrodynamics as “the spacetime approach”, since he conceived of quantum interactions as a sum of all possible paths through spacetime. Hence we might say the totality of spacetime serves to mediate quantum interactions. Hints of this approach could already be seen during the discussions of Bohr and Einstein in 1927, when they considered the one-slit and two-slit experiment, which they might have noticed could be generalized to any number of interposed diaphragms with any number of slits, ultimately leading to Feynman’s view of a particle’s propagation as the superposition of all possible combinations of null segments through spacetime.

It’s interesting to consider the loci of spacetime events that are null-separated from two or more given events. Note that the spatial volume enclosed by such a “mediating surface”, i.e., the surface null-separated from each of two events on the worldline of a timelike particle, is a maximum when evaluated with respect to its rest frame. When evaluated relative to any other inertial frame the volume is reduced due to spatial contraction, consistent with the increased relativistic mass, and the fact that the effective range of mediating particles is inversely proportional to their mass. (For example, the electromagnetic force mediated by massless photons has infinite range, whereas the strong nuclear force has a very limited range because it is mediated by massive particles.)

Naturally the structures of alternating lightcones and shells transform under change of coordinates in exactly the same way as in Lorentz’s model of the “corresponding states” of elementary particles discussed in Section 1.5. Lorentz had simply conjectured that the forces maintaining the shape of elementary particles must conform to this lightcone structure of electromagnetic waves and therefore must transform similarly. In a sense, the relativistic Schrödinger wave equation and Dirac's general argument for light-like propagation of all physical entities (based on the combination of relativity and quantum mechanics as discussed in Section 9.9) provide the modern justification for Lorentz's conjecture.

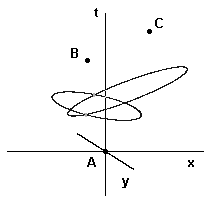
We can also consider the mediating surfaces for more than two events. For example, if two coupled particles separate at event A and interact with particles at events B and C respectively, the interaction is as shown below:

The loci of events null-separated from events A and B intersects with the locus of point null-separated from A and C at the two points of intersection of the two circles, but in full four-dimensional spacetime the intersection of two such loci is a closed circle. Note that the two surfaces intersect if and only if B and C are spacelike separated. We might speculate that EPR correlations correspond to consistency conditions for the wave function on this circular locus.

The locus of null-separated points for two lightlike-separated events is a degenerate quadratic surface, namely, a straight line as represented by the segment AB below:

The "surface area" of this locus (the intersection of the two cones) is necessarily zero, corresponding to the fact that these interactions represent the transits of massless particles. For two spacelike-separated events the mediating locus is a two-part hyperboloid surface, represented by the hyperbola shown at the intersection of two null cones below

This hyperboloid surface has infinite area, which suggests that any interaction between spacelike separated events would correspond to the transit of an infinitely massive particle. However, recalling that a pseudosphere can be represented as a sphere with purely imaginary radius, we might speculate that interactions involving virtual pairs of particles over spacelike intervals – within the limits imposed by the uncertainty relations – may correspond to such hyperboloid mediating surfaces.

In a closed universe the "open" hyperboloid surfaces might have to be regarded as finite, albeit extremely large. In a much smaller closed universe − as is thought to have existed immediately following the big bang − there may be have been an era in which the "hyperboloid" surfaces had areas comparable to the ellipsoid surfaces, in which case the distinction between spacelike and time-like interactions would have been blurred.

In addition to the usual 3+1 dimensions, one could argue that spacetime operationally entails two more "curled up" dimensions of angular orientation to represent the possible directions in space. The motivation for treating these as dimensions in their own right arises from the non-transitive topology of the pseudo-Riemannian manifold. Each point [t,x,y,z] actually consists of a two-dimensional orientation space, which can be parameterized (for any fixed frame) in terms of ordinary angular coordinates θ and ϕ. Then each point in the six-dimensional space with coordinates [x,y,z,t,θ,ϕ] is a terminus for a unique pair of spacetime rays, one forward and one backward in time. We might imagine a tiny computer at each of these points, reading its input from the two rays and sending (matched conservative) outputs on the two rays, as illustrated below in the xyt space:

The point at the origin of these two views is on the mediating surface of events A and B. Each point in this space acts purely locally on the basis of purely local information. Specifying a preferred polarity for the two null rays terminating at each point in the 6D space, we automatically preclude causal loops and restrict information flow to the future null cone, while still preserving the symmetry of wave propagation. Both components of a wave-pair could be regarded as "advanced", in the sense that they originate on a spherical surface, one emanating forward and one backward in time, but both converge inward on the particles involved in the interaction.

According to this view, the "unoccupied points" of spacetime are elements of the 6D space, whereas an event or particle is an element of the 4D space (t,x,y,z). In effect an event is the union of all the pairs of rays terminating at each point (x,y,z). We saw in Section 2.6 that the transformations of θ and ϕ under Lorentzian boosts are beautifully handled by linear fractional functions applied to their stereometric mappings on the complex plane.

One possible objection to the idea that quantum interactions occur “locally” between null-separated events is based on the observation that, although every point on the mediating surface is null-separated from each of the interacting events, they are spacelike-separated from each other, and hence unable to communicate or coordinate the generation of two equal and opposite outgoing quantum waves (one forward in time and one backward in time). However, communication between those events may not be required, because although the points on the mediating locus are not communicating with each other, each of them is in receipt of identical information from the two interaction events A and B. Each point responds independently based on its local input, and the combined effect of the entire locus responding to the same information is a coherent pair of waves.

Another possible objection to the "spacetime mediation" view of quantum mechanics is that it evidently relies on temporally symmetric propagation of quantum waves. This objection can't be made on strictly mathematical grounds, because both Maxwell's equations and the (relativistic) Schrödinger equation actually are temporally symmetric. The objection seems to be motivated by the idea that temporally symmetric propagation automatically implies that every event is causally implicated in every other event, if not directly by individual interactions then by a chain of interactions, making impossible the kind of separability that seems essential for any meaningful physical theory. However, as we've seen, the spacetime mediation view actually leads naturally to the conclusion that interactions between spacelike-separated events are either impossible or else of a very different (virtual) character than interactions along time-like intervals. Moreover, the stipulation of a preferred polarity for the ray pairs terminating at each point is sufficient to preclude causal loops.

Incidentally, two of the best known anecdotes about Paul Dirac can both be seen as expressions of the requirement for the initiation of any action to be contingent on its conclusion, just as the light from Tetrode's star can only be emitted if there is a suitable reception, though it may be an eye located in the far distant future. One of these stories was told by Heisenberg regarding a journey that he and Dirac made together in 1929, and appears as the epigraph of this chapter. The second story refers to when the young Dirac was visiting Bohr in Copenhagen. Dirac later recalled that during his stay he and Bohr had many long talks, during which Bohr did practically all the talking. At one point while Bohr was dictating some remarks, he stopped in mid-sentence and told Dirac that he was having trouble finishing the sentence. Dirac said

At school I was taught never to start a sentence without knowing the end of it.

Return to Table of Contents