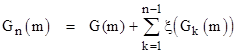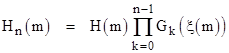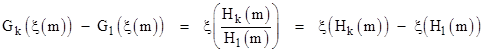Part 3:  Iterated Functions

Given any two binary operations a(x,y) and b(x,y), suppose there is a function f such that

For any set of such functions, define the auxiliary functions

It's easy to see that u and v are "conjugates", in the sense that

Slightly less obvious is the fact that the nth compositions of u(x) and v(x), denoted by u_n(x) and v_n(x) respectively, are also conjugates, i.e.,

This identity is sometimes useful in simplifying computations. To illustrate, consider the case a(x,y) = xy, b(x,y) = x + y, f(x) = ln(x). Here the auxiliary functions are

Taking an initial x value of 10, the first few iterations of u(x) are

10.000000,  23.025851,  72.223287,  309.098522

Beginning with an initial x value of f(10) = 2.302585 the first few iterations of v(x) are

2.302585,  3.136617,  4.279762,  5.733660

Comparing these sequences of iterates, we see that the function f maps from one to the other. For example, we have f(309.098522) = 5.733660. More generally, if we take f(x) = log_b(x) for any base b, and define the auxiliary functions

then the nth iterates of these functions, denoted by u_n(x) and v_n(x), are related by the equation

The logarithm has a unique inverse (although the log itself is multi-valued for negative arguments), so this allows us to give u_n(x) explicitly in terms of v_n(log_b(x)) as

In general, any function f(x) possessing an "addition rule" can be adapted to this process. A few examples are summarized below.

This procedure can also be applied to additive number-theoretic functions. For example, consider the case

where ξ(x) is the "sum-of-prime-factors" function. In this case the auxiliary

functions are

Beginning with an initial value of 10, the first few iterations of H are

10,  70,  980,  22540,  1036840

Beginning with an initial value of ξ(10) = 7, the first few iterations of G give

7,  14,  23,  46,  71

and we can verify that ξ(1036840) = 71.

Proposition 12:  Letting H_n(N) and G_n(N) denote the nth iterations of the functions H(N) = Nξ(N) and G(N) = N + ξ(N), we have

and

for any integer m.

Proof:  It's easy to show by induction that

for any integer a. Now suppose that

Then we have

The quantity in the square brackets equals G_k(ξ(m)), as can be seen by setting a = ξ(m) in the earlier expression for G_k(a), so the proof is completed by induction. ◊

Corollary 12-1:  For any non-negative integers n and m we have

Proof:  By Proposition 12 we have

and

Combining these two equations gives

Rearranging terms gives

The right hand side equals zero, so the left side also equals zero for any non-negative integer k. ◊

Return to Table of Contents