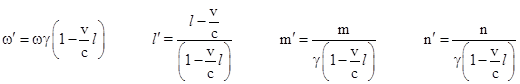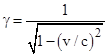Did Einstein Misunderstand Aberration?

One of the most common misconceptions regarding special relativity is the idea that there is something wrong with its treatment of stellar aberration. This is usually expressed in terms of the incoming rays from binary star systems, which, according to the common misunderstanding, ought to exhibit widely varying amounts of aberration due to the differences in the velocities of the revolving stars. Since such variations are not observed, the anti-relativityist claims that special relativity is thereby falsified. Tony Rothman's 2003 book entitled "Everything's Relative" presents an interesting variation on this familiar theme. Rothman agrees with the claim that Einstein's treatment of aberration was faulty, but he (Rothman) exonerates special relativity itself, and concludes instead that Einstein simply "didn't understand his own theory". Furthermore, he alleges that "Einstein's mistake" was repeated by Pauli and a host of others.

Rothman has alluded to this subject more than once. For example, in response to comments on another of his essays ("Lost in Einstein's Shadow") in "The New Scientist", he wrote

There are mistakes in the 1905 relativity paper, including a serious conceptual error regarding the bending of starlight ("aberration"), one of the phenomena Einstein created his theory to explain.

It’s ironic to find the phrase “serious conceptual error” followed so closely by a description of aberration as “the bending of starlight”, considering that aberration doesn’t involve “bending”. Setting that aside, Rothman’s charge is particularly startling in view of the fact that the clarification of the purely kinematic basis of aberration is usually seen as one of the key insights of special relativity. Indeed, it was the relativistic Doppler and aberration effects that led Einstein to the mass-energy equivalence relation (E = mc²), and that also confirmed the crucial correspondence between energy and frequency (E = hν) of light quanta.

Is Rothman correct? Did Einstein misunderstand and/or mis-represent stellar aberration in his 1905 paper? One point in Rothman's argument can be answered immediately. He says “no one recognizes the rather large blunder in Einstein’s exposition” because "no one bothers to read the original papers any more". But surely this is preposterous. Einstein's paper "On the Electrodynamics of Moving Bodies" has been, and continues to be, one of the most avidly scrutinized documents ever written. Whole books have been devoted to parsing its every word. (Has any physicist not read it?) If the paper contains a "serious conceptual error" regarding one of its central results, and if this has gone unnoticed by scientists and scholars for over 100 years, it cannot be attributed to neglect of the original text.

Turning to the substantive issue, the specific aspect of stellar aberration that Rothman believes Einstein misunderstood is the physical meaning of the velocity “v” appearing in the familiar formula

where ϕ is the angle between the path of a light pulse and the positive x axis in terms of one system K of inertial coordinates xyt, and ϕ′ is the angle of the same path and the x′ axis of another system k of inertial coordinates x′y′t′ moving with speed v in the positive x direction relative to K. Rothman echoes the perennial anti-relativity claim that if v is taken as the relative velocity between the source and receiver (in other words, if K and k are the rest frames of the source and receiver respectively), then the relativistic aberration formula is contradicted by observations of binary stars. The “reasoning” behind this erroneous claim is that the stars in binary systems have large velocities in opposite directions as they orbit each other, so the relative velocity between the Earth and the stars is significantly different, and hence, according to this (erroneous) reasoning, if we define v as the relative velocity of the rest frames of the source and the observer, equation (1) predicts that the stars of a binary system ought to appear at widely separate locations in the sky as viewed from the Earth, because the value of v is very different for the two stars.

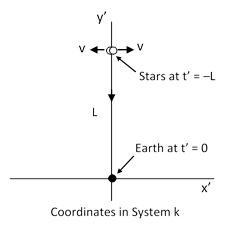
The error in this reasoning is the failure to take into account the aberration of the angle ϕ, i.e., the line of sight to the Earth as seen by the revolving stars. This can be illustrated with a simple example. Suppose the Earth is momentarily resting at the origin x′ = 0, y′ = 0, t′ = 0 of an inertial coordinate system k. At a prior time t′ = -L (in units such that c = 1) suppose two stars are located at x′ = 0, y′ = L, and they are moving in opposite directions with velocities +v and –v along a line parallel to the x′ axis, as depicted below.

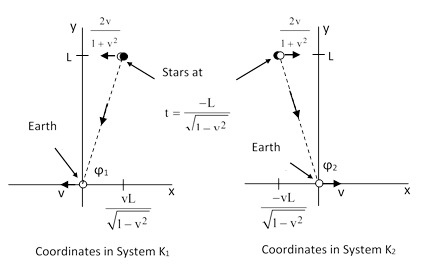
The anti-relativityist claims that Einstein’s formula predicts the two stars will appear at significantly different angles to an observer on the Earth, because the Earth is moving with the speeds –v and +v relative to the inertial coordinate systems in which the stars are at rest (at, say, the time of emission).  But this claim is false. To show this, let K₁ and K₂ be inertial coordinate systems with the same origins as k but in terms of which the stars are at rest when they emit the pulses of light seen at the origin on Earth. Since the origins of our coordinate systems coincide at the reception event, the coordinates of that event in terms of the K₁ system are x = 0, y = 0, t = 0, and by the Lorentz transformation the coordinates of the emission event in terms of the K₁ system (which, remember, is moving with speed +v in the positive x′ direction relative to k) are

Therefore, letting ϕ₁ denote the angle between the x axis and the path of light from the star to the Earth in terms of the K₁ coordinate system, we have cos(ϕ₁) = v. Substituting this into equation (1), we find that cos(ϕ′) = 0, confirming that the light path is perpendicular to the x′ axis in terms of the k system in which the Earth is momentarily at rest. Repeating this calculation for the star moving with velocity –v, we find that the path in terms of the K₂ coordinate system has the angle ϕ₂ such that cos(ϕ₂) = –v, and substituting this into equation (1) gives again cos(ϕ′) = 0. Thus the two components of the binary star system both appear on Earth at the same angular location according to the angle transformation formula of special relativity. Of course, the Earth appears at two significantly different angles to observers on those two stars, due to the different rest frames of those stars. The figure below shows the paths of the light rays in terms of the inertial coordinate systems K₁ and K₂.

When equation (1) is applied to the light pulse coming from the first star to the Earth, taking K₁ as the system in terms of which the Earth is moving at speed –v and the light path makes an angle ϕ₁ with the x axis, we get the angle ϕ′ = 90 degrees for the angle of the light path in terms of the k coordinate system co-moving with the Earth. Likewise when equation (1) is applied to the light pulse coming from the second star to the Earth, taking K₂ as the system in terms of which the Earth is moving at speed +v and the light path makes an angle ϕ₂ with the x axis, we get (again) the angle ϕ′ = 90 degrees for the angle of the light path in terms of the k coordinate system co-moving with the Earth. Thus there is no paradox at all, and the predictions of special relativity are perfectly consistent with observation.

Of course, the same formula (1) works for converting angles between any two systems of inertial coordinates. In every case, v is always the velocity of the coordinate system k relative to some other coordinate system K. The source of light need not be at rest in K, and in fact the receiver need not be at rest in k. It is merely by convention, when speaking about stellar aberration, that we traditionally choose K so that the source is (momentarily) at rest in K. But this tradition dates back to the days when the distant stars were thought to be “fixed” (stationary) in the firmament. Now that we know the stars have significant relative motions, and some are even being accelerated rapidly (as in binary systems), the motivation for choosing K as the momentary rest frame of a star is greatly reduced. The anti-relativityists overlook the fact that a star in orbital motion around another star will not be continuously at rest in terms of any single system of inertial coordinates. The momentarily co-moving inertial coordinate system of such a star is continuously changing. As a result, the “line of sight” to the Earth is undergoing aberration as viewed from the revolving star, just as the “line of sight” to the star is undergoing aberration as viewed from the revolving Earth. Indeed we see that equation (1) is reciprocal, in the sense that it can also be written in the equivalent form

which has the same form as (1) except that v is replaced with –v and ϕ is transposed with ϕ′. Like equation (1), this equation gives the correct relationship between the angles of the light pulse in terms of any two systems of inertial coordinates, such as the instantaneous rest frames of a source and a receiver, although if those entities are accelerating we must specify a time, since in that case they are not continuously at rest in terms of any single inertial coordinate system. As a star in a binary system moves in its orbit, it is momentarily at rest in a sequence of different inertial reference frames, so the “source frame” K is continually changing, and the angle ϕ for any given k and ϕ′ is changing accordingly. Likewise if we identify k with the co-moving rest frame of the Earth, then k is continually changing as the Earth moves in its orbit. For any choice of frames K and k, the values of ϕ, ϕ′ and v are related by equation (1), and equivalently by (2). Needless to say, it’s most convenient to choose a stable reference system for K, such as the rest frame of a roughly inertial object, e.g., the center of mass of the binary system, or the center of mass of our own solar system, in terms of which ϕ is virtually constant for light from distant stars. (Note that the light path between two given events depends only on the positions of those events, by definition, not on the velocities of the emitting or receiving entities.) With this more convenient choice of K, v is the velocity of the Earth relative to that stable reference system K, making the calculations much easier. But it’s important to realize that this is merely for convenience. The relativistic formula for transformation of angles gives the correct results for any two systems of inertial coordinates. In summary, there is no validity whatsoever to the claim that the equation for the transformation of angles in special relativity is flawed.

As noted above, Rothman agrees that special relativity is fine, but he claims that Einstein himself misunderstood aberration. Actually, there seems to have been some modulation of Rothman’s view of Einstein’s actual culpability, because in the book “Everything’s Relative” he says “Einstein clearly assumes that the velocity involved is the relative velocity between the Earth and the star” (which Rothman, like the anti-relativityists, erroneously thinks is wrong), whereas in the paper “Reference Frames for Stellar Aberration” he is more circumspect, saying only that

Einstein gets aberration from the Doppler shift and does not further define the velocity in his equation, leading one to wonder whether his own lack of clarity was the source of the subsequent confusion.

That sentence leads me to wonder if Rothman was describing himself when he said “no one bothers to read the original papers any more”. First, Einstein did not “get aberration from the Doppler shift” (which doesn’t even make sense), he derived both the Doppler shift and the aberration formula from the Lorentz transformation. Second, it is untrue that Einstein “does not further define the velocity in his equation”. Einstein was actually quite careful and explicit about the relevant value of v appearing in the Doppler and aberration formulas. He wrote

In the system K, very far from the origin of coordinates, let there be a source of electrodynamic waves, which in a part of space containing the origin of coordinates may be represented to a sufficient degree of approximation by the equations [A = A₀ sin(F)] where

Here [A] are the vectors defining the amplitude of the wave train, and l,m,n the direction-cosines of the wave normals. We wish to know the constitution of these waves when they are examined by an observer at rest in the moving system k [defined previously as moving at the speed v in the positive x direction with respect to K].

(For brevity, I’ve used “A” to denote the components of the electric and magnetic vectors, which Einstein spelled out explicitly.) As an aside, notice that Einstein does not say the source of the waves is at rest in K, whereas he does explicitly stipulate that the observer is at rest in k. Of course, the source of the waves may be at rest in K, but it need not be. The state of motion of the source has no bearing on Einstein’s derivation. He defines a plane wave near the origin in terms of the K coordinate system (x,y,z,t), giving both its frequency w and the direction-cosines l,m,n of the wave normal with respect to these coordinates, and then proceeds to determine the frequency w′ and direction-cosines l′,m′,n′ with respect to the k coordinate system (ξ,η,ζ,τ) which is moving at the speed v relative to K. He does this simply by applying the appropriate transformations to the field components and the space and time coordinates, giving the phase angle

where

and

This is clear and unambiguous. A single transformation determines both the Doppler shift and the aberration effect. In neither case does the state of motion of the source enter into consideration. Einstein simply describes how a plane wave at a certain time near the origin, characterized by a certain frequency and direction with respect to one system of inertial coordinates (K), is characterized by a different frequency and direction with respect to another system of inertial coordinates (k), given that the latter is moving with velocity v relative to the former. This is the only meaning of the “v” appearing in these formulas. We can use these formulas to transform the angle of a light path between any two inertial coordinate systems. This is a perfectly clear and correct derivation of the relativistic transformation of angles.

It’s important to note that the direction of a plane wave arriving at the origin at a given time depends on the position of the source at the time emission, but not on the state of motion of the source, which is why the motion of the source has no bearing on the derivation of the aberration formula. The velocity v is explicitly stated to be the velocity of the observer’s rest frame k with respect to the frame of reference K in terms of which the plane wave takes a specified form near the origin. This is unobjectionable, and disproves that claim that there is “a serious conceptual error” in Einstein’s understanding of aberration.

Of course, if the source is at rest in K, then v also happens to be the velocity of the observer relative to the rest frame of the source, but, as we’ve seen, the equation is correct, regardless of whether the source is at rest in K or not. Now, given the above results describing how a plane wave transforms from one system of coordinates to another, Einstein enunciates a corollary, to show how this angle transformation formula accounts for the phenomenon of stellar aberration, saying

…it follows that if an observer moving with velocity v relatively to an infinitely distant source of light… in such a way that the connecting line “source-observer” makes an angle ϕ with the velocity of the observer referred to a system of coordinates which is at rest relatively to the source of light… [and] if we call the angle between the wave normal (direction of the ray) in the moving system and the connecting line “source-observer” ϕ′, the equation for l′ assumes the form

This equation expresses the law of aberration in its most general form.

The symbols l and l′ were already defined as the direction cosines of the wave normal with respect to the two relatively moving systems of coordinates, so there is nothing new in this equation. Einstein has merely re-stated the previously derived equation, writing the direction cosines explicitly in terms of the angles, and identifying the system K with the rest frame of the source (which, as we’ve seen, is perfectly permissible).

Before addressing the substance of these words, we need to make note of an obvious misprint in the text. The quoted words define ϕ as the angle between the light ray and the observer’s velocity, both evaluated with respect to K, consistent with how that angle was defined previously. However, according to Einstein’s previous derivation, the angle ϕ′ is defined in the analogous way with respect to k, whereas the words in the just quoted passage define ϕ′ as the angle between the light ray and the “connecting line source-observer”. (I bolded these words in the quote above). This is obviously a misprint, because the wave normal and the source-observer line both signify the direction of the ray, and neither refers to the direction of motion of k (the observer) with respect to K. Also, note that the words “connecting line source-observer” appear in the immediately preceding sentence. Presumably were inadvertently duplicated in the next sentence. Sure enough, the assessment of this as a transcription error is confirmed by a pre-print of Einstein’s 1905 paper (in possession of G. Holton) showing some corrections in Einstein’s own hand, and the phrase “connecting line source-observer” is crossed out and replaced with “direction of motion”, consistent with how Einstein had defined it previously. The page also shows another correction, one that actually found its way into the later published versions, but the above correction evidently did not. In fact, it wasn’t included in the widely re-printed “Meuthen/Dover” collection (1923), although it has been noted in other editions, including those of A. I. Miller, John Stachel, and in Einstein’s collected papers. Note also that in Einstein’s review paper of 1907, containing essentially the same derivation, the angles are described correctly.

This misprint in the 1905 paper surely doesn’t suggest a “serious conceptual error”, especially since the correct wording appears elsewhere in the same paper. Also, this misprint isn’t even mentioned by Rothman, et al. In fact, his “Reference Frames” paper doesn’t actually refer to any specific wording from Einstein’s paper, but presumably he would argue that Einstein blundered in the above quoted passage by specifying that the infinitely distant source is at rest in the system K, leading to the pseudo-paradox of the binary stars, which Rothman evidently regards as a genuine paradox. As we’ve seen, the relativistic formula for the transformation of angles is perfectly correct for any two inertial coordinate systems K and k, regardless of whether the source is at rest in K. The pseudo-paradox of the binary stars is simply due to the failure to account for the fact that there are two different K frames in that case (one for each star), with two different values of ϕ, both leading to the same value of ϕ′ in k. Thus the case when K is the rest frame of the source at some specified instant does not present any problems at all. This was the traditional choice when discussing aberration (going back to Bradley, who regarded the distant stars as “fixed”), but as we’ve discussed, it isn’t the most convenient choice when dealing with accelerated sources. A more convenient choice for analyzing the light from a binary star system would be the rest frame of the center of mass of the system, or the center of mass of our own solar system, but this is entirely a matter of convenience, since the formula (1) is valid for any choice of K and k.

By the way, I emphasized the words “infinitely distant” in the above passage, because this condition ensures that any bounded transverse motions of the source have no effect on the direction of the “source-observer” line. Thus no oscillatory motions of binary star components (for example) have any relevance. It’s also worth noting that binary star systems are not the only sources for which the insignificance of bounded oscillatory motion is present. The same is true for the agitated motions of the individual atoms comprising any source of electromagnetic waves, not to mention the rotations of macroscopic objects, and so on.

In summary, Einstein’s analysis of aberration in his 1905 paper on special relativity is unobjectionable – in fact, it’s fairly elegant, especially in comparison with all earlier (and many later) treatments.

Ironically, after declaring Einstein guilty of a “serious conceptual error” and of not understanding his own theory as it pertains to aberration, the description of aberration advanced by Rothman, et al, is conceptually incorrect. They conclude rather laboriously that

…the parameter v in the Lorentz transformation is interpreted as the difference between the velocity of the earth at the different points in spacetime in which the observations are made.

Now, it’s admittedly possible to apply the formula for the transformation angles in the way suggested by this statement. We can define K as the co-moving inertial coordinate system of the Earth at a certain time t₁, and k as the inertial coordinate system that will be co-moving with the Earth at a time t₂ six months later. On this basis, the parameter v is indeed the difference between the velocities of the Earth at different times. However, on this basis, equation (1) tells us the relationship between the values of ϕ(t₁) and ϕ′(t₁), i.e., the angles of the path of a single pulse of light expressed in terms of two different systems of inertial coordinates. What we actually observe on Earth is something different, namely, the values of ϕ′(t₁) and ϕ′(t₂), which are the angles of incidence of two different pulses of light at two different times. It so happens that, if ϕ(t₂) = ϕ(t₁), meaning that the angle of incidence of the starlight at time t₂ is the same as it was at time t₁, both evaluated in terms of the coordinate system co-moving with the Earth at time t₁, then the observed difference between ϕ′(t₁) and ϕ′(t₂) will be equal to the difference between ϕ(t₁) and ϕ′(t₁). But this need not be the case (due to parallax, for example, or secular movement of the source), so Rothman’s suggested interpretation is strictly incorrect.

Contrary to Rothman’s suggestion, the parameter v in the Lorentz transformation, and in the angle transformation formula (1), is nothing other than what Einstein said it was, namely, the velocity between two system of inertial coordinates, and the formula gives the relationship between the angles ϕ and ϕ′ of the path of a single pulse of light in terms of those two coordinate systems.

In general, the difference in the angle of incidence of light from a given object can be due to secular changes in the relative position of that object, or to changes in the receiver’s state of motion, or some combination of both. We merely surmise from our observations that the directions to the distant stars in terms of the rest frame of the center of mass of each star system, or the center of mass of our own solar system, or any other convenient system of inertial coordinates, are not changing appreciably over the time span of interest, and that the stars are so distant that parallax due to the Earth’s motion around the Sun is small, and therefore the observed changes in the angles of incidence can be attributed to the changes in the Earth’s state of motion relative to the chosen system of reference. Thus to compute the aberration of starlight on Earth we apply equation (1) at two different conditions at times t₁ and t₂, with a single angle ϕ but with the two extreme values of the Earth’s velocity relative to our chosen reference system, to give the two values  ϕ′(t₁) and ϕ′(t₂), and by convention we refer to the difference between these values as “the aberration of starlight”.

Naturally we’re free to define the term “absolute instantaneous aberration” as the quantity ϕ′– ϕ, where those angles are defined for the rest frames of the receiver and source respectively, but if the source is in accelerated motion this is not a very sensible definition. Bradley originally conceived of the stars as “fixed”, i.e., stationary, so it was natural to think in terms of absolute aberration, taking K as the absolute rest frame, in terms of which the angles are the “true” angles. But now that we know stars are in accelerated motion, it no longer makes sense to define the instantaneous rest frame of a star at any given moment as the absolute true rest frame. Thus the concept of absolute aberration has lost its meaning. For convenience we may choose to specify a single reference frame for the entire duration of the light passing from emitter to receiver, but this obviously cannot coincide with the instantaneous co-moving inertial coordinate systems of stars in binary systems (for example).

Fortunately, on a macroscopic level, we often find that sources of light move uniformly on average over some suitable time scale. If a light source is undergoing bounded oscillations with a period that is short compared with the transit time of the light, then it’s convenient to work in terms of the average state of motion over those oscillations. This is true whether we are talking about the agitated motions of the molecules on the surface of a single radiating body, or the orbital motions of the components of a binary star system. On this basis we can often still apply the traditional notion of absolute aberration (as opposed to changes in aberration). The velocity parameter v in the aberration equation is then interpreted as the velocity of the observer with respect to the inertial coordinates in terms of which the source is at rest on average over the time scale of the light transit time. Notice that, for example, aberration of the light from one component of a binary star system as judged from a planet orbiting that star would be defined relative to the rest frame of the star itself during a small portion of its orbit, whereas judged from the Earth many light years away it is defined relative to the center of mass of the binary system. The time scales for the light transit are very different in these two cases, so the relevant mean motion of the source is different.

We saw above that an important feature of the correct explanation of relativistic aberration is the fact that in special relativity “transverseness” of motion is not transitive. If a pulse of light is emitted perpendicular to the source’s motion relative to the receiver’s rest frame, it is not generally perpendicular to the receiver’s motion relative to the sources rest frame. In a sense, the equivalence of mass and energy can be traced directly to this fact – which of course did not escape Einstein’s notice, and led to a brief follow-up paper in September of 1905. This is why the charge that Einstein misunderstood relativistic aberration is so absurd. The profound understanding of the relativistic aberration/Doppler effect and its implications was arguably his greatest achievement.

Regarding the charge that subsequent expositors of special relativity, notably Pauli, have “repeated Einstein’s mistake”, a review of these expositions shows that they are perfectly correct. The mistake is on the part of readers who erroneously fail to take into account the complete relativity and reciprocity of aberration. Admittedly some expositions might be more clear if they described this in detail, explicitly addressing the misconception about binary stars, etc., but these things are rather obvious to anyone who has grasped the basics of special relativity – and of course incomprehensible to anyone who hasn’t.

Return to MathPages Main Menu