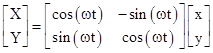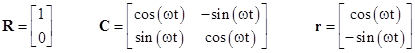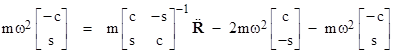Inertial Forces and D’Alembert’s Principle

The distinction between what Aristotle called natural motions and violent motions has always played a central role in the formulation and interpretation of physical theories. Natural motions are regarded as passive “states” that need no active external influence to sustain them, whereas violent motions are considered to be the result of some external influence. Obviously this invokes other distinctions, such as the one between external and internal, which pre-supposes a degree of separability or isolation between different entities. Moreover, there is a distinction between active and passive effects, which relies on the tacit assumption of super-natural (i.e., violent) agencies, related to the concepts of vitalism and free will. It took thousands of years for people to arrive at the modern scientific conception of inertial motion, according to which any motion at constant speed in a straight line is considered natural, and such motion will continue indefinitely until some external influence is applied. Of course, the concepts of “constant speed” and “straight line” must be defined in order for this formulation to have meaning, and ultimately the only possible definition is a circular one: we define straight lines and constant speeds based on the characteristics of the motions of objects that are not subjected to external influence, but we know they are not subjected to external influence only from the fact that they are moving at constant speed in a straight line.

This circularity can be seen in the modern treatment of (classical) dynamics, where the “laws of motion” are defined in terms of a special class of space and time coordinate systems, called inertial coordinates, but those systems are effectively defined by the laws of motion. In other words, these coordinate systems are aligned with the inertial behavior of objects, so that motions are “unaccelerated” when they occur purely as a result of inertia. Here the word “unaccelerated” means that the second derivative (with respect to time) of the space coordinates is zero. If the second derivatives of the space coordinates of an object do not vanish, we attribute this to some external influence, which we call a force. In principle, we could define any class of motions as “natural”, and prefer the corresponding class of coordinate systems in terms of which those “natural” motions are unaccelerated. Any deviations from unaccelerated motion (in terms of these coordinates) would then be interpreted as being due to the application of external forces. This is the essential content of D’Alembert’s principle, which asserts that we can with equal validity describe physical phenomena in terms of any system of coordinates, regardless of whether they are inertial coordinates, provided we introduce suitable forces. This idea was implicit in the Principia, and was a forerunner of Einstein’s equivalence principle.

Our preference for inertial coordinate systems is motivated by the fact that, within the context of such systems, the forces necessary to account for all observed motions are very few in number, and can be characterized very simply in terms of observable relations between objects. Thus inertial coordinates constitute an organizing principle – and a phenomenally successful one. Nevertheless, this way of organizing our knowledge is still the result of a choice, because it isn’t the only possible way of understanding and describing our experience. In fact, we sometimes find it more convenient to work (and think) in terms of non-inertial coordinate systems, usually in circumstances where the motions of interest happen to be easily characterized in terms of such coordinates. For example, if we are describing events taking place inside an automobile, we may find it convenient to describe those events in terms of coordinates that are co-moving with the automobile, even if the automobile is undergoing non-inertial motion. However, when we do this, we must recognize the “inertial forces”, since we are no longer using coordinates that are defined in such a way as to make those forces vanish. Some people refer to inertial forces as “fictitious”, partly because they are an artifact of our choice of coordinate systems. However, ultimately all forces are artifacts of our coordinate systems, in the sense that we could define coordinates in terms of which any particular force “vanishes”, i.e., in terms of which any object subject to that force moves in such a way that the second derivatives of its space coordinates with respect to time are zero. Hence this is not a valid reason to regard inertial forces as any more (or less) “fictitious” than any others.

Of course, inertial forces differ from the usual forces in other respects, such as the fact that we do not (normally) associate inertial forces with any interactions with other bodies. Indeed this is one of the most important factors underlying our decision to formulate physical laws of terms of inertial coordinates. But two things can be said against this rationale. First, we do not actually know whether or not inertia is ultimately due to interactions between bodies. As emphasized by Ernst Mach (for example), we do not know what would be the result of holding an elevator car motionless and accelerating the rest of the universe. Would this produce “inertial” acceleration on an occupant of the elevator? Lacking a theory of the origin of inertia, any claim that inertial forces are not due to interactions, and/or that inertial forces do not satisfy the law of reaction, are conjectural. Second, even if we accept that inertial forces differ from non-inertial forces in not being due to interactions, there is still no a prior reason to classify them as “fictitious”. The use of that term merely bespeaks a somewhat naïve chauvinism for one particular way of organizing our knowledge.

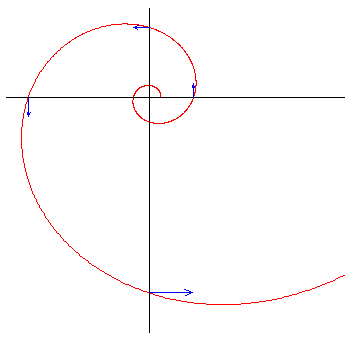
Another important distinction involving inertial forces (and one that is sometimes overlooked) is between passive and active transformations. Consider a bead attached to a stationary frictionless rod, so that the bead is free to slide along the length of the rod. If we describe these objects in terms of a rotating coordinate system centered at one end of the rod, the bead’s distance from the end of the rod does not change, even though the rod is rotating in terms of the rotating coordinate system. On the other hand, if we use an inertial coordinate system, but we set the rod into rotation about one end, the bead will be accelerated, and it’s distance from the center of rotation will increase at an accelerating rate. In both cases the rod is accelerating relative to the coordinate system, but in one case it is “really” the coordinate system that is accelerating, whereas in the other case it is the rod. These two cases lead to very different physical outcomes. In the first case, with the non-inertial coordinate system, we must account for inertial forces, i.e., the centrifugal and Coriolis forces, but there is no change in the radial position of the bead. In the second case, there are no inertial forces to consider, because we are working in terms of an inertial coordinate system, and yet in this case the bead is accelerated outwardly from the center of rotation. This may seem puzzling at first, because clearly the frictionless rod is incapable of exerting any radial force on the bead, and yet when we rotate the rod the bead is clearly compelled to move outwardly along the rod at an accelerating rate. Some would interpret this as signifying that a “real” centrifugal force, arising from the rotation of the rod, is being applied to the bead.  In a sense this is true, because when the rod is pointing due North it is accelerating the bead in the westward direction, and shortly thereafter the rod is pointing West, so the rod actually was accelerating the bead in the outward direction, albeit out of phase by 90 degrees, as illustrated in the figure below.

For a rod rotating at constant angular speed, the bead’s radial distance from the center of rotation is proportional to cosh(ωt), the radial velocity is proportional to ωsinh(ωt), and the radial acceleration is proportional to ω²cosh(ωt). So, although the bead’s acceleration is always strictly circumferential at any given instant, it is nevertheless being forced away from the center. This is the basis of operation of centrifugal pumps.

We should also note that as the bead acquires an outward speed, it’s angular speed would tend to decrease if it weren’t accelerated tangentially by the rod. Since a tangentially-moving object possesses radially outward kinematic acceleration away from the center, the inertia of the object (if regarded as being due to an interaction with the distant galaxies, for example) does really represent an “outward” force. Furthermore, since this kinematic acceleration is proportional to the square of the tangential speed, by accelerating the bead tangentially the rod is acting to increase the outward acceleration of the bead. This is a real physical effect, described in terms of an inertial coordinate system, not an artifact of a non-inertial coordinate system. Rotation of the rod really does compel the bead to accelerate outward, even though the force applied by the rod is always purely perpendicular to the rod’s current orientation (which defines the current “outward” direction). These considerations are perhaps what convinces some people that the centrifugal force is a “real” force arising somehow from the tangential force, the inertia of the object (whatever its origin), and the kinematics of the situation.

It’s worth mentioning that much of the confusion is due not to rotation, but simply to the use of polar coordinates, as can be seen from the fact that the “outward” direction depends on location, so there is an inherent ambiguity as to whether an object is being subjected to “outward” force, especially when it is being subjected to forces in all directions at different times. The fact that the direction of the force is always 90 degrees out of phase from the “outward” direction is arguably not sufficient reason to deny that the object is indeed being subjected to a “real” outward (i.e., centrifugal) force. It is certainly being compelled to recede from the center at an accelerating rate (as described in terms of an inertial coordinate system), so there is at least some plausibility to this argument. Certainly if inertia were attributed to an interaction with the distant masses in the universe, there would be no question that the bead sliding on a rotating rod was subjected to a “real” outward force, and presumably the distant masses would be (very slightly) drawn inward. But lacking any definite explanation for the origin of inertia, the question of the “reality” of inertial forces is unanswerable (if not meaningless).

Setting aside the perplexing questions about “reality” and the ultimate origin of inertia, people are sometimes puzzled by the simple mathematics of the preceding example, in which with a stationary rod, described in terms of rotating coordinates, there is a centrifugal force on the bead, and yet the bead’s radial position doesn’t change. The explanation is that there is another component of inertial force, called the Coriolis force, that cancels out the centrifugal force in such cases. To see explicitly how this works, let X,Y,Z denote an inertial coordinate system, and let x,y,z denote a different Cartesian coordinate system, defined in such a way that if the position vector to a certain particle is R with respect to the X,Y,Z system, then the position vector r with respect to the x,y,z system is given by R = Cr for some time-dependent rotation matrix C. Differentiating this relation by the chain rule, we get the absolute velocity of the particle in terms of the velocity relative to the x,y,z coordinates as

Differentiating again, we get the absolute acceleration of the particle in terms of the position, velocity, and accelerations relative to the x,y,z coordinates

The second term on the right hand side is the Coriolis acceleration, and the third term is the centrifugal acceleration. Multiplying through by m (signifying the mass of the particle) and the inverse of C, and re-arranging terms, we get

The left hand side is the mass times the acceleration in terms of the x,y,z coordinates, and if those were inertial coordinates we would expect this to equal the sum of the “real” forces on the particle, represented by the first term on the right hand side. If the transformation matrix C is constant, then the x,y,z coordinates are inertial, and in that case the second and third terms on the right hand side are each zero. However, if the transformation matrix is not constant, those two terms are non-zero, and they represent the Coriolis force and the centrifugal force respectively, i.e., the “inertial forces” that must be included to account for the use of non-inertial coordinates.

To illustrate, suppose a particle is stationary at location R = (1,0,0)^T in terms of the inertial coordinates, and suppose the x,y,z coordinates have the same origin but are rotating about the Z axis at the constant angular speed ω. We can ignore the z axis, and write the relationship between the coordinate systems as

Thus we have

Substituting into equation (1) we get

where we’ve abbreviated the sine and cosine of ωt as simply s and c respectively. Again, the left hand side is the total inertial “force” on the particle with respect to the x,y,z coordinates, because it is the mass times the acceleration of the particle in terms of these coordinates (with respect to which the particle is moving in a unit circle about the origin). In our example, the particle is stationary in the inertial coordinates (meaning R is constant), so we know that the “real” forces applied to the particle, represented by the first term on the right hand side, are zero. Therefore, in this case, the only “forces” on the particle are the inertial forces, i.e., we have

Hence in this case the Coriolis force is twice size of the centrifugal force, and the former points inwards whereas the latter points outwards, yielding a net inertial force of –mω²r, (noting that the second derivative of r equals –r in this case) just as we would expect. This inward fictitious force corresponds to the fact that the particle, which is stationary in terms of the inertial coordinates, is moving in a circle in terms of the rotating coordinates, and hence is undergoing a net fictitious centripetal acceleration.

As noted above, inertial forces also appear in stationary curvilinear coordinate systems, the most familiar of which are stationary polar coordinates r,θ, related to inertial coordinates X,Y by the equations X = r cos(θ) and Y = r sin(θ). Differentiating each of these twice with respect to time, we get

where c and s now signify the cosine and sine of θ. Solving these for the second derivatives of r and θ, we get

If we multiply through by the mass m of a particle, and let ϕ denote the angular direction of the force of magnitude F associated with the second derivatives of X and Y, we can write this as

For a particle motionless with respect to the inertial X,Y,Z coordinates, the first and second derivatives of r and θ are zero, so the only “accelerations” would be due to F. On the other hand, a particle of mass m moving at uniform angular speed ω in a circle must be subject to a centripetal force of constant magnitude directed at an angle opposite the angular position of the particle, which implies ϕ = θ + π. In this case we also have the positive value mrω², which represents the centrifugal force, so the second derivative of r is zero, as expected.

Obviously we could multiply through these equations by the mass of a particle, and refer to each term as a “force” instead of an acceleration. Whether we regard these “forces” and the corresponding accelerations as real or fictitious is ultimately a matter of definition. If we define the word “acceleration” to mean the second derivative (with respect to time) of a position coordinate, then the second derivatives of r and θ are indeed genuine accelerations. On the other hand, if we apply the (admittedly circular) Newtonian definition of acceleration, according to which a true acceleration is a deviation from inertial motion, then we would not necessarily consider the second derivatives of arbitrary positional coordinates to be true accelerations. The article on Curved Coordinates and Fictitious Forces presents further discussion of this topic in a more general context.

Return to MathPages Main Menu