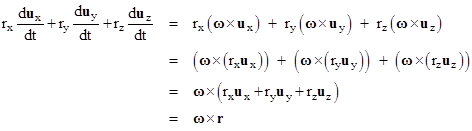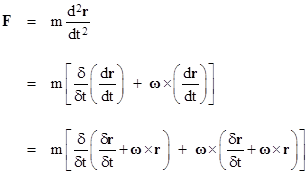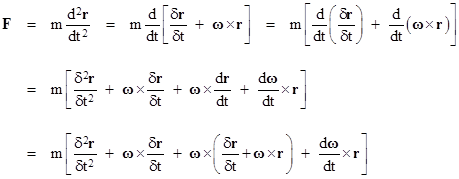Centripetal and Centrifugal Forces

The Latin word “petitus” means inclining towards, and the Latin word “fugo” means to drive away. Hence the European scientists of the 17th century (who customarily composed their scholarly treatise in Latin) used the terms centripetal and centrifugal to refer to effects directed towards or away from (respectively) some central point. For example, the effect of the Sun’s gravity was said to be centripetal because it compels an orbiting planet toward the center of the orbit. On the other hand, the inertia of an orbiting object is said to have a centrifugal effect, because continued motion in a straight line would tend to carry the object away from the center. In a circular orbit these two effects are equal, so the object maintains a constant distance from the center.

The meanings of the words “centripetal” (inward) and “centrifugal” (outward) are fairly clear and free of ambiguity, provided both the “central” point and the location of the effect are adequately specified. However, these words are often conjoined with the word “force”, the meaning of which has been the subject of philosophical debate since ancient times. As a result, the meanings of the terms “centripetal force” and (especially) “centrifugal force” have sometimes been obscured.

According to Newton, a material object moves with constant velocity unless acted upon by a force, in which case the object undergoes an acceleration proportional to the applied force. More precisely, a system of coordinates is defined such that the space coordinates of every free particle are linear functions of the time coordinate. This leads to rectilinear inertial coordinate systems. In terms of such coordinates, the applied force is proportional to the second time derivative of the space coordinates. In addition, Newton asserted that “to any action there is always an opposite and equal reaction”. For example, the Sun acts on a planet by applying a centripetal force that continually accelerates the planet, holding it in a (roughly) circular orbit; and likewise the planet acts on the Sun by applying a centripetal force that continually accelerates the Sun, holding it in a (roughly) circular orbit. Newton was the first to recognize that the center of the Sun is not actually the center of the orbits of the planets, because the Sun itself orbits the true center of mass of the solar system. Of course, the radius of the Sun’s orbit is extremely small compared with the radii of the planetary orbits, but nevertheless the Sun does “orbit the Earth” in this sense, just as the Earth orbits the Sun. (Eppur si muove!)

Notice that we have not mentioned any “centrifugal force” in our description of orbiting bodies. This is consistent with the fact that the only forces involved are the mutual forces of gravity that the Sun and planet exert on each other, and these forces compel each body toward the other, and therefore toward the center of their orbits. Now, one might argue that there is some ambiguity in the direction of the forces based on the ambiguity in the location of those forces. For example, the planet is “pulling” the Sun inward (i.e., toward their common center of mass) by a force acting in the direction from the Sun toward the planet. If we regard this force as existing at the Sun’s location, then the indicated direction is indeed “inward”, but if we regard this force as existing at the planet, then the indicated direction of the force is actually “outward”. On that basis, we might claim that the force of the planet on the Sun should be called centrifugal rather than centripetal, and the same argument could be made for the force of the Sun on the planet. This ambiguity is especially acute in the context of the Newton-Cotes concept of gravity as an instantaneous “force at a distance”, which makes the location of forces indeterminate. However, it is generally agreed (in the Newtonian context) to identify a force with the associated action, i.e., the deviation of an object from an inertial path. Thus the force exerted by the planet on the Sun is regarded as being located at the Sun, and therefore the force is properly called centripetal (as is the force of the Sun on the planet).

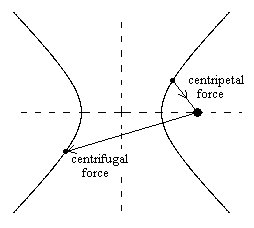
There are, however, examples of genuine centrifugal forces. For example, two electrons repel each other, so the forces could be termed centrifugal, meaning the forces tend to drive the objects away from the “center”. Of course, in such cases, the concept of a “center” is less clear than in the case of closed orbital motion, but it still seems legitimate to regard the source of the repulsion as the “center”. Interestingly, Newton included a brief mention of this kind of “centrifugal force” in the Principia. First he explained that the motion of an object subject to a central force, whose magnitude varies inversely as the square of the distance from the “central” point, is a conic section with the central point at one focus. Then, in Book I, Section 3, Proposition 12, after proving this for one branch of a hyperbolic path, he notes that “if this centripetal force is turned into a centrifugal force, a body will move in the opposite branch of the hyperbola”, as illustrated in the figure below.

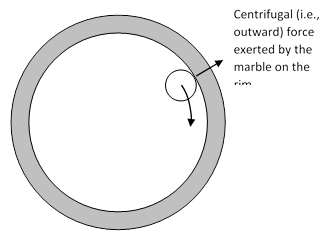
Another situation in which centrifugal forces arise is in cases exemplified by a marble rolling around the stationary circular housing of a roulette “wheel”. This is similar to the case of a planet moving in a circular orbit, except that the reaction force exerted by the marble on the housing is applied at the point of contact, and hence is directed outwardly from that point, as shown in the figure below.

Thus the marble exerts a genuine centrifugal (i.e., outward) force on the housing, balancing the centripetal (i.e., inward) force exerted by the housing on the marble, so that the marble maintains a constant distance from the center of the wheel. Indeed Newton used the term “centrifugal force” to describe precisely this kind of force in Principia. (See the Scholium following Proposition 4 of Section 2, Book 1.) However, it must be remembered that Newton was writing in Latin, using the word centrifugal simply as a literally descriptive adjective signifying the direction away from the center.

Confusion about the meaning of the term “centrifugal force” in modern English usage comes about because that Latin word has been adopted to refer to something entirely different than the literal outward force described above. Just to re-iterate, in the preceding example the housing exerts a centripetal force on the marble, which causes the marble to undergo centripetal acceleration, continually diverting it inward from its inertial path, and compelling it to follow a circular path. This is the only force (in the Newtonian sense of the word) being applied to the marble. Admittedly the marble is, in turn, exerting a centrifugal force on the housing, but there is no centrifugal (i.e., outward) force on the marble. The confusion arises if we try to view the situation in terms of a system of coordinates rotating (about the center of the roulette wheel) in such a way that the marble is stationary. The housing is still exerting an inward force on the marble and yet, in terms of this rotating coordinate system, the marble is not accelerating. Needless to say, this is not a violation of Newton’s second law, because that law – written in homogeneous form so that force is proportional to the second derivative of the position coordinate with respect to the time coordinate - applies only to motions described in terms of inertial coordinate systems, whereas our rotating coordinate system is clearly not an inertial coordinate system.

We might just choose to leave it at that, but in some circumstances there is a desire to make use of Newton’s laws (formally) while working in terms of a non-inertial coordinate system. This can actually be done by introducing certain fictitious forces. For example, in the rotating system of coordinates we must posit a centrifugal force on every (stationary) particle, dependent on the rotational speed of the coordinate system, and varying in proportion to the distance from the center of rotation. This fictitious force exactly balances the inward force on the marble, so the absence of acceleration (in terms of these rotating coordinates) is made formally consistent with the homogeneous and isotropic form of Newton’s second law. In other words, we explain why the marble is not accelerating by saying that the net radial force on the marble is zero. Of course, in the inertial sense, the marble actually is accelerating inward, but we are accounting for one fiction by means of another. We are pretending, first, that the marble is not accelerating, and second, that the marble is subject to an outward (centrifugal) force – which explains why it is “not accelerating”.

In general we can consider a rigid Cartesian coordinate system xyzt whose origin is co-located with the origin of some inertial coordinate system XYZt, and whose absolute angular velocity is ω(t). If an arbitrary vector q is stationary in the rotating system, it follows that the derivative of q with respect to time for the inertial system is given by the cross product

Now let r be an arbitrary vector, not necessarily stationary in the rotating system, and let the scalars  r_x(t), r_y(t), r_z(t) be the magnitudes of its components (as functions of time) relative to the rotating system. Thus we have

where u_x, u_y, u_z are the unit vectors (also functions of time) of the xyz coordinate axes. Differentiating each term with the chain rule and re-arranging the resulting terms, we get the derivative of r with respect to t relative to the inertial coordinates:

The expression in the first parentheses is simply the derivative of the r vector in terms of the rotating coordinates. To simplify the expression in the second parentheses, note that the unit vectors are stationary in the rotating frame, so we can use the identity dq/dt = ω x q to write

Thus the derivative of r in terms of the inertial XYZ coordinates is related to the derivative in terms of the rotating xyz coordinates by

This applies to any vector. Hereafter for convenience we will omit the subscripts and simply denote derivative in terms of the inertial XYZ frame with ordinary “d” symbols, and derivative in terms of the rotating xyz frame with “δ” symbols.

Now, recall that Newton’s law of motion for a particle of mass m is

To express this in terms of a reference frame rotating with angular velocity ω, we need only apply equation (2) twice, as follows.

Expanding this expression, noting that the chain rule applies to differentiation of cross products, and that the cross product is distributive over addition, we have

The first term on the right hand side looks like the right side of Newton’s law in an inertial frame, except that the differentiations are in terms of the rotating coordinates, so the second derivative does not represent the absolute acceleration. The second term on the right side is sometimes called the Euler acceleration, and is proportional to the rate of change of the rotating frame’s angular velocity. The above expression indicates that this derivative is evaluated in terms of the rotating coordinate system, but an equally valid application of formula (2) gives

Expanding and collecting terms, this gives

This is identical to equation (4), except that the indicated derivative of ω is taken with respect to the inertial coordinates. It follows that

meaning that the vector corresponding to the rate of change of the angular velocity of the rotating frame is the same, regardless of whether the derivative is evaluated in terms of the inertial frame or the rotating frame. On some level this might seem vaguely paradoxical, because one might think that the rotating frame is always stationary with respect to itself, by definition. Thus we have [ω]_xyz = 0 at all times, and yet [dω/dt]_xyz need not be zero. Of course, there’s nothing surprising about the fact that a function may be zero while its derivative is non-zero, but this condition would ordinarily exist only for an instant, not for a continuous span of time. This is a subtle but profound example of the difference between inertial and non-inertial systems of reference.

The third term on the right side of (5) is commonly called the Coriolis acceleration, and the fourth term is the centripetal (inward) acceleration. Occasionally people find it convenient to bring some of the acceleration terms over to the “force” side of the equation (with negated signs) can treat them as fictitious forces. If all the accelerations are brought over, the right hand side becomes zero, and we have dynamic equilibrium, but it’s also common to leave the first term on the right hand side, and just bring over the remaining terms. In that case Newton’s law is written in the form

where

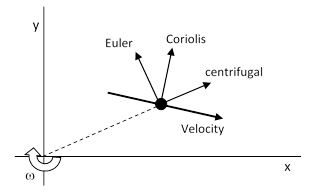
To illustrate, consider a reference frame rotating about the z axis, and suppose a particle of mass m is moving with some velocity v in the xy plane. Since each of the fictitious forces is given by a cross product involving the angular velocity vector or its derivative, it follows that they are all in the xy plane, except possibly for the Euler force in case the axis of rotation is changing. The above equations show that the Coriolis force is perpendicular to the velocity of the particle, with magnitude 2mωr where r is the distance from the origin. The centrifugal force points directly away from the origin (i.e., the axis of rotation) with magnitude mω²r. Lastly, the Euler acceleration is perpendicular to the radial direction, with magnitude mr(dω/dt), and lies in the xy plane if the axis of rotation is fixed. This is illustrated in the figure below.

Notice that the centripetal acceleration term becomes a centrifugal force when brought over to the force side of the equation. Newton himself made use of the term “centrifugal force” in this fictitious sense. The Scholium following Proposition 4 at the beginning of Book 3 explains the reasoning by which Newton realized that the moon is held in its orbit around the earth by the force of gravity, i.e., the same force that pulls terrestrial objects (like apples) to the ground. He imagines several moons orbiting the earth at different radii, and notes that Kepler’s law for orbiting bodies implies that the inward acceleration is proportional to the inverse square of the orbital radius. If we then imagine the lowest of these moons being at the radius of the mountain tops on earth, we find that its downward acceleration (in accord with Kepler’s law) has the very same value as the downward acceleration of an apple at the top of the mountain. We must therefore conclude that the inward force on orbiting bodies like the moon must be nothing other than the very same force of gravity that pulls apples to the ground. Newton wrote

This centripetal force [implied by Kepler’s law] would cause this little moon, if it were deprived of all the motion with which it had remained in its orbit, to descend to the earth – as a result of the absence of the centrifugal force with which it had remained in its orbit – and to do so with the same velocity with which heavy bodies fall on the tops of those mountains…

Here we see that Newton has tacitly asserted the existence of a centrifugal (outward) force given to the “little moon” by its orbital motion, and he conceives of this centrifugal force as balancing the centripetal force, thereby maintaining the moon at its normal distance. This illustrates how psychologically natural it is for us to “abstract away” the acceleration of an object in circular motion and to conceive of a fictitious (in Newtonian terms) outward force on the object to balance the real inward force. (The same tendency can be seen underlying Galileo’s difficulty in freeing himself from the idea that purely circular motion represented a kind of force-free motion – the idea that prevented him from clearly articulating the rectilinear law of inertia.)

Thus Newton uses the term “centrifugal force” in the Principia to describe three very distinct concepts. First, he uses it to refer to a hypothetical repulsive force (such as the force between two electrons), which would result in a hyperbolic path, accelerating away from the source of the “central” repulsive force. Second, he uses the term to refer to the outward force exerted by a revolving object on some framework (such as the force exerted by a roulette marble on the housing). Third, he uses the term to refer to the “fictitious” outward force on a revolving object when viewed from a revolving frame of reference. A fourth context in which the concept of “centrifugal force” may arise is when phenomena are described in terms of curved coordinate systems, such as polar coordinates. Such non-linear coordinate systems are not inertial in the spatial sense, even though they may be static (i.e., not accelerating), as discussed in the note on Curved Coordinate Systems and Fictitious Forces. A fifth usage of the term “centrifugal force” occurs when the inertial forces on an object, relative to a momentarily co-moving inertial frame, are de-composed into tangent and normal components (in the osculating plane). The normal component is called centrifugal force. There is no Coriolis force with this convention, because the particle is always at rest with respect to the co-moving inertial coordinates. Needless to say, all these usages are very closely related, and differ only by context and convention.

Of course, if the origin of our rotating coordinate system was undergoing translational acceleration, there would be an additional acceleration term in equation (4), and that term could also be brought over to the left side and treated as a fictitious force. Interestingly, a fictitious force of that kind is found to behave exactly like a “real” homogeneous gravitational field. This fact, due to the proportionality of inertial and gravitational mass established by Galileo and Newton, served as the inspiration for the Equivalence Principle, which led Einstein to the general theory of relativity. According to that theory there is no local physical difference between a “real gravitational force” and a “fictitious inertial force”, because free motion in a gravitational field is understood to be purely inertial motion (locally). In other words, the gravitational field and the inertial field are one and the same, characterized by the ten metric tensor coefficients at each point of spacetime. For more on this topic, see Vis Inertiae.

The question of whether inertial forces are “real” or merely “fictitious” has sometimes been passionately debated – as is usual for matters of definition. One hears it stated confidently that fictitious forces may be distinguished from real forces by the (alleged) fact that the latter are mutually exerted between objects whereas the former – being supposedly just an artifact of a choice of an accelerating coordinate system, are not. However, strictly speaking, the assertion that inertia is intrinsic to each body, rather than being a result of interactions with other objects in the universe, is only a conjecture. Some scientists, notably Ernst Mach, have maintained that inertia actually does arise from interactions with other objects, albeit interactions of a kind different from those with which we are most familiar. Indeed Einstein's general theory of relativity provides some (limited) support for this view, since the inertial behavior of each object is affected by the presence of other objects. Whether it is possible to account for all inertia in this way is an open question, and depends on subtle issues of boundary conditions and the topology of the universe. (A prominent advocate of this view was the late American physicist John Wheeler.) In the context of the "standard model" of quantum field theory, there have been intense efforts to detect the so-called Higgs particle, which according to the standard model of particle physics is an excitation of a field (the Higgs field) responsible for the inertial masses of most other elementary particles. The Large Hadron Collider (LHC) has reported that the Higgs particle has indeed been detected. Nevertheless, the Higgs mechanism does not explain or provide a mechanism for inertia itself, it “merely” represents the mechanism whereby energetic fields (which already have inertia proportional to their energy) acquire a rest frame with a speed below the speed of light, and hence some of their energy takes on the form of rest mass. The Higgs mechanism does not account for why energy has inertia in the first place. Thus, we still have no definitive theory of the origin of inertia. It is customary to disregard the issue, especially in elementary discussions, and simply accept uncritically the Newtonian view that there is such a thing as absolute acceleration (and we know it when we see it), independent of the mean state of motion of all the matter in the universe. Only on this naïve basis can we assert that inertial forces are “fictitious”, i.e., that they do not arise from interactions. General relativity clearly undermines this distinction between real and fictitious forces, because it teaches us that the metric field responsible for the “real” force of gravity is identical with the metric field responsible for the “fictitious” force of inertia.

Return to MathPages Main Menu