Cosmological Horizons

                                          Soft you now,

The fair Ophelia! – Nymph, in thy orisons

Be all my sins remembered.

If we conceive of the universe as a closed spherical space expanding in time, it may or may not be the case that a light pulse could circumnavigate the universe, depending on the rate at which the space is expanding. Let R(t) denote the radius of the universe at the epoch t, and let α denote a coordinate that signifies the angular position of a given particle on the circumference of the universe. The speed of a particle at the epoch t is

Notice that, even though R is a function of t, we do not regard d(Rα)/dt as the speed, because the “movement” in the radial direction is perpendicular to all the spatial directions. For a pulse of light, we have v equal to a constant c, and we can determine the equation of the path by re-writing the above equation as

Integrating both sides from t₀ to t₁, and putting α(t₀) = 0, we get

If the rate of expansion is uniform, meaning that R(t) = kt for some constant k, then we get

Thus the path of a pulse of light in spacetime is a logarithmic spiral, which is to say, the angular position α as a function of the radial position r is of the form

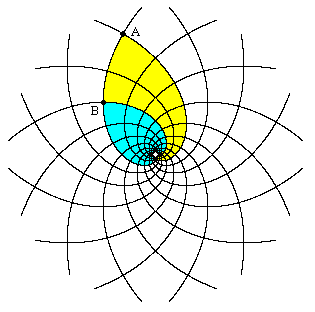
In this case the paths of light pulses in both directions are illustrated in the figure below.

The yellow and blue shaded regions together represent the causal past of event A, and the blue shaded region is the causal past of event B. This figure shows the partial ordering of events, i.e., if C is in the causal past of B, and B is in the causal past of A, then C is in the causal past of A. Each light pulse circles the origin infinitely many times in both the forward and backward directions, although at distances that increase (or decrease) exponentially. The worldlines of typical galaxies would be purely radial lines. In this model universe there are no cosmological event horizons, because every galaxy is “visible” to every other galaxy. In fact, each galaxy can (in principle) see infinitely many instances of each other galaxy.

On the other hand, if a spherical universe is expanding at an increasing rate, there may be limits to visibility. The diagram below shows the path of a light pulse for several consecutive time intervals in such a universe.

A light pulse is emitted at event A when the universe has radius R₀. The pulse travels a spatial distance L to the event B over an interval of time Δt, by which time the radius of the universe has increased to R₁. The pulse then travels another spatial distance L over the same duration of time Δt, and arrives at event C, at which time the radius of the universe is R₂. The pulse then travels another spatial distance L over the same duration of time Δt, and arrives at event D, at which time the radius of the universe is R₃. And so on. Letting α₁ denote the angular travel of the pulse during the first interval (as it travels from A to B), we have L = α₁R₁, and likewise L = α₂R₂ and L = α₃R₃. If R increases exponentially with time, we have R_j+1/R_j = k for some constant k, and therefore α_j+1/α_j = k. Thus the total angular travel for the light pulse is

Therefore, if k is less than 1, the pulse of light will travel only a limited angular distance around the circumference of the expanding universe. Regions of the universe outside that angular arc cannot be influenced by event A, and likewise there are galaxies at the present epoch that can never affect the galaxy the originated this light pulse at A. The boundary – which of course is spherical – between events that can send a signal to the galaxy at A and events that cannot, is called an event horizon.

In general, we will have an event horizon if and only if there is an upper limit to the value of α that is given by equation (1). In other words, if we increase the upper limit t₁ on the integration to infinity, and the integral still yields just a finite angular travel, a light pulse emitted at t₀ cannot reach any point beyond that angular displacement around the circumference of the universe. Of course, for a closed spherical universe, if the finite value of α exceeds 2π, the light pulse can circumnavigate the universe at least once, so we might prefer to define the necessary condition for a horizon to be that the integral

yields a value less than 2π. To illustrate, consider a universe that is expanding at an exponentially increasing rate, i.e., we have R(t) = Ae^kt for some positive constants A and k. Equation (1) gives

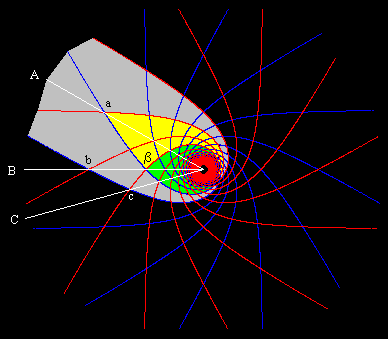
which is the equation of a hyperbolic spiral. A typical case is shown in the figure below.

The radial lines marked A, B, and C represent the worldlines of typical galaxies. The shaded yellow and green region is the causal past of galaxy A at event a. This region, combined with the shaded gray region, represents the portion of the universe that can send a signal to galaxy A. The boundary of the shaded gray region is the event horizon of A. We note that galaxy C passes outside this horizon at event c, and thereafter it cannot communicate with A. On the other hand, galaxy B remains within the event horizon of A until reaching event b, when it too passes outside. Eventually every other galaxy passes outside the event horizon of A.

One benefit of presenting horizons in a spacetime diagram, rather than in a purely spatial diagram, is that it makes clear the transitive nature of the partial ordering of events. In other words, if event b is inside the event horizon of event a, and if event c is inside the event horizon of b, then c is inside the event horizon of a. Lack of clarity on this point sometimes leads to confusion over the fact that galaxy C can be outside the horizon of galaxy A while it is inside the horizon of galaxy B, which is still inside the horizon of A. If horizons were purely spatial, this would seem to imply that C could send a signal to B, which could then relay the signal on to A, and hence C can send a signal to A, contradicting the fact that C is outside the event horizon of A. Needless to say, this reasoning is invalid, because it overlooks the fact that if C is outside the event horizon of A, then, even if B is presently inside the event horizon of A, by the time a signal from C reaches B, the latter must have passed outside of the event horizon of A.

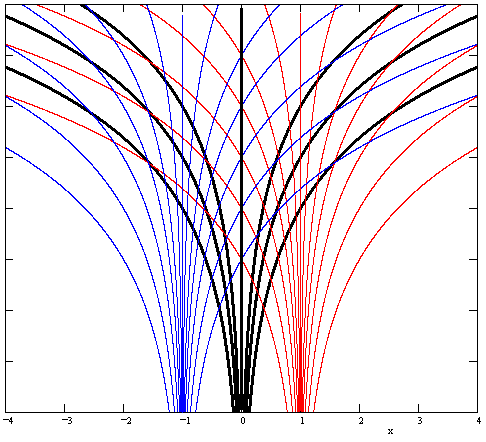
The preceding discussion has focused on spherical closed universes, but the notion of an event horizon can also apply to open unbounded universes, although the graphical depiction in such cases is different, and R(t) simply signifies a scale factor, rather than the actual radius of the universe. The figure below shows one such representation, for an infinite universe with an exponentially increasing scale factor R(t).

This figure actually shows only a small number of the galaxy worldlines and lightlines. The vertical axis is cosmological time. Each of the three “fountains” is actually infinitely wide, and they completely overlap each other for all times. The black curves represent the worldlines of typical galaxies. The blue and red curves represent the paths of light pulses emitted in the “rightward” and “leftward” directions respectively.  The equations for these curves are of the form

This diagram makes the event horizon of the central galaxy explicit at the locations x = −1 and x = +1, where light pulses emitted from a galaxy proceed “vertically”, and never intersect with the worldline of the central galaxy. Of course, these light pulses do eventually intersect with every closer galaxy, since those move outward. To transform to a system of coordinates in which some other galaxy is at the center, we simply offset the x coordinate in each of the three expressions.

In universes with maximally symmetric subspaces we can choose global coordinates r, θ, ϕ, t such that the spacetime metric takes the form

where k is a constant, and we can scale the units so that k is either +1, 0, or −1. This is called the Robertson-Walker metric. The function R(t) is fairly arbitrary, but if we impose the field equations of general relativity we get three possible forms of R(t), depending on the value of k. The simplest case is k = 0, which forms the boundary between closed and open universes (within this class of models). The resulting model, which expands forever from an initial singularity at t = 0, is known as the Einstein-deSitter model. In this model we have

Inserting this into equation (1), we get

As t₁ increases there is no limit to the amount of angular travel, so there is no event horizon in this model. Every event on every galaxy is eventually visible to every other galaxy. Notice, however, that the angular travel from t₀ = 0 to any given t₁ is finite, and equals zero at t₁ = 0. This signifies that, initially, no particle can have received a signal from any other particle at a different angular position, and by a given time t a particle has received light only from particles that are within an “cosmological angular distance” of

Multiplying this angular distance by R(t) gives the corresponding proper distance

This is called the particle horizon. A given particle cannot have received any signal (by the time t) from any particle that is presently further away than this distance. It can be shown that all three of the cases k = −1, 0, and +1 contain particle horizons, but, ironically, only the re-collapsing universe corresponding to K = +1 contains an event horizon. This may seem counter-intuitive, since one might think that as the “radius” of the universe shrinks during the collapsing phase, any light signals would be able to reach all points in the universe. In a sense they do, but only at the instant of final collapse. At any instant prior to that, there are regions that have never been visible to a given galaxy. To see this, note that for the Robertson-Walker metric in the equatorial plane θ = 0, the path of a light pulse (dτ = 0) satisfies

Therefore the cosmological angular travel for a pulse of light by equation (1) is

where the right-hand integral is evaluated along the path of a light pulse emitted at t₀,r₀ and received at t₁,r₁. With k = −1 or 0, the right-hand integral can achieve arbitrarily large values, but with k = +1 the integral is asin(r), which is bounded, so there is an event horizon. The light pulses converging on an observer can’t out-run the collapsing universe.

Essentially the existence or non-existence of event and particle horizons depends on whether the initial and final states of the universe are spacelike or null. Three different possibilities are illustrated schematically in the figures below.

Figure (a) represents a universe in which there are neither event horizons nor particle horizons. Every timelike worldline proceeds from the initial (lower) state to the final (upper) ultimate state, and the universe is spanned by light signals emanating from and converging on those states. Figure (b) represents a universe with a space-like initial state but a null final state. In this universe, a worldline becomes visible to a given particle only once the past lightcone of that particle encompasses that worldline. Hence we have a particle horizon, as indicated by the red null lines. However, there is no event horizon, because every event is eventually visible to every particle. Figure (c) represents a universe with a null initial state but a spacelike final state, so there is no particle horizon, but there is an event horizon, because eventually every other particle’s worldline passes outside the past light cone of a given particle at the final state, which implies that the given particle will never see those other worldlines once they have outside that horizon, represented by the green null lines. Lastly, Figure (d) represents a universe in which both the initial and the final states are spacelike. In this universe, there are both particle horizons and event horizons. The figure shows the past light cone of the central figure in red, indicating the boundary of the events that have been visible to the central particle up to the given time. Also shown (in green) is the past light cone of the central particle at its ultimate state. This is the event horizon of for the central worldline.

Return to MathPages Main Menu