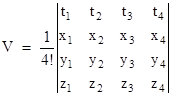Classical Electrons and Spacetime Volume

Maxwell’s equations predict the electric and magnetic fields associated with a given distribution of charge (and currents), but don’t constrain how charge is distributed, nor even whether the distribution is continuous or discrete. Only during the last decade of the 19th century did it gradually become clear that electric charge appears only in the form of identical discrete entities, those with negative charge being called electrons. Still, the structure of an electron was mysterious, because there seemed to be only two possibilities, each of which was considered problematic: either an electron is a singular concentration of charge at an infinitesimal point, or else it consists of a continuous distribution of charge spread over some finite region. A point-like charge was difficult to accept, because it seemed to imply infinite field strength at the point where the charge is located, and hence infinite potential energy. The alternative was for electrons to have some finite size. The most common idea was that an electron consists of a spherical shell of uniform charge, but this immediately raised the problem of explaining why the separate parts of the negative charge didn’t repel each other and fly apart. Obviously Maxwell’s equations – being linear – cannot account for any stable configuration of charge, so some other (non-electromagnetic) force must be present to hold the particle together.

Several competing models for an elementary charged particle were put forward during the early years of the 20th century. The three best known were those of Max Abraham, Alfred Bucherer and Paul Langevin, and Hendrik Lorentz. Abraham proposed a perfectly rigid spherical electron, whereas the models of Bucherer-Langevin and Lorentz were deformable, i.e., their equilibrium shapes varied with their velocity through the ether. Lorentz’s electron was subject to the Fitzgerald contraction in the direction of motion, but exhibited no change in size in the transverse directions (in agreement with the result of Heaviside and Searle in 1892 for the shape of a charged shell necessary to produce the same field as a point charge), whereas the Bucherer-Langevin model contracted in the direction of motion and expanded in the transverse directions so as to maintain a constant spatial volume. Strictly speaking, all three of these models required some unknown force to hold the parts of the electron together, but Abraham argued that this force could be ignored when dealing with his rigid model, since the forces maintaining the structure did not displace the surface, and hence performed no work. A similar argument could be made for the model of Bucherer-Langevin because, although it was deformable, it too had constant volume, so no net work was done by the forces maintaining the structure (even though, in this case, some work was transferred through the electron from the contracted portion of the surface to the expanded portions). In contrast, the volume of the Lorentz electron evidently changed when the electron was set in motion, so work was performed by the structure-preserving force. Abraham criticized Lorentz’s model on this account, pointing out that it led to two different predictions for the “longitudinal mass”, one based on momentum (which is unaffected by the structure-preserving force) and another based on energy.

All of these models predicted that the electromagnetic mass increased with speed, and if experiments showed that the entire mass of an electron varied in this way, many scientists were prepared to conclude that all mass was electromagnetic in origin. Furthermore, the hope was that measurements of the precise acceleration of rapidly moving charged particles would reveal which of the electron models was correct. All these considerations were soon cast in a new light by Einstein’s special theory of relativity, which made it clear that (on the assumption of relativity) all mass transforms in the same way as electromagnetic mass, so the longitudinal mass variation predicted by Lorentz’s theory was to be expected regardless of the structure of the electron, and regardless of whether the electron’s mass was or was not of purely electromagnetic origin. The famous factor of 4/3 in the expression for the electron’s energy and hence it’s rest mass is due to the pressure, called Poincare’s pressure, required to hold the electron’s charge together. In his Palermo paper of 1905 (published in 1906), Poincare wrote

The advantage of Langevin’s theory is that it requires only electromagnetic forces, and bonds; it is, however, incompatible with the postulate of relativity. This is what Lorentz showed, and this is what I found in turn using a different method, which calls on principles of group theory. We must return therefore to Lorentz’s theory, but if we want to do this and avoid intolerable contradictions, we must posit the existence of a special force that explains both the [Fitzgerald] contraction, and the constancy of two of the axes. I sought to determine this force, and found that it may be assimilated to a constant external pressure on the deformable and compressible electron, whose work is proportional to the electron’s change in volume.

With the advent of quantum mechanics, the old attempts to model the electron in terms of classical electrodynamics began to seem even less relevant, as the electron came to be regarded as point-like in quantum field theory, where the problems of infinite self-energy were handled by re-normalization. Max Born, who was a young researcher toward the end of the classical period, and who later became one of the founders of quantum mechanics, gives an interesting account in his essay “Physics and Relativity”:

Today this formula [for the energy and mass of the electron] is taken so much for granted that you can hardly imagine the acerbity of the controversies which raged around it. In 1901 W. Kaufmann in Göttingen had by an investigation of the electromagnetic deflection of fast cathode rays first established the fact that the mass of the electron depends on its velocity. Max Abraham took up this challenge and showed that the electromagnetic mass, as introduced by J. J. Thomson, i.e., the self-energy of the electron's own field, properly developed for high velocities did indeed depend on velocity. He assumed the electron to be a rigid sphere; but later he also modified his theory by taking account of the Lorentz-Fitzgerald contraction, and obtained exactly the formula which Lorentz had already found by a simpler reasoning. As a matter of fact, the velocity dependence of energy and of mass has nothing at all to do with the structure of the body considered, but is a general [generic] relativistic effect. Before this became clear, many theoreticians – including G. Herglotz, P. Hertz, A. Sommerfeld, and others – wrote voluminous, not to say monstrous, papers on the electromagnetic self-energy of the rigid electron. My first scientific attempt was also in this direction…  Today all these efforts appear rather wasted; quantum theory has shifted the point of view, and at present the tendency is to circumvent the problem of self-energy rather than to solve it. But one day it will return to the center of the scene.

Incidentally, we can see in retrospect that, like the models of Abraham and Bucherer-Langevin, the electron model of Lorentz also maintained constant volume in a manner of speaking, provided we evaluate not the spatial volume but the spacetime volume. In fact, this follows from the most basic premises – i.e., linearity, homogeneity, isotropy, reciprocity – of the transformation from one system of inertial coordinates to another. To make explicit the notion that the structure of an electron is maintained by structure-preserving forces that transform in the same way as electromagnetic forces, we could conceive of a Lorentzian electron as oscillating spherical shell, as shown in the figure below (with one of the spatial dimensions suppressed).

We regard one instance of the electron as a cycle of this expansion and contraction (these occurring at the speed of light), and the spacetime “volume” of the electron is the content of spacetime contained within the shell during this cycle. The projected areas in the xt plane are the same for both the stationary and the moving electron, and from this fact we can derive the full Lorentz transformation. To prove that the projected areas are equal, note that the size of the enclosed region is the same in the two transverse spatial directions (i.e., the y and z axes), so the ratio of the areas in the xt projections will be the same as the ratio of the spacetime volumes. Thus we need only show that the enclosed spacetime volumes are equal.

Any region of spacetime (given a fixed relationship between the units of space and time) can be partitioned into four-dimensional simplexes, each defined by five vertices (events) in spacetime. For any given simplex, by homogeneity, we can displace our origin so that one of the vertices is at the origin, and the other four vertices v_j = {t_j,x_j,y_j,z_j} for j=1,2,3,4 represent vectors emanating from the origin. It’s easy to show that the spacetime volume of the simplex is given by

We now subject all the events on the surface of this simplex to a linear transformation, which gives another simplex in the transformed coordinates, defined by the transformed vertices, and the spacetime volume in terms of these new coordinates will again be given by a determinant of the form shown above, except with the transformed coordinates replacing the original coordinates. Thus, letting X and X′ denote the 4x4 matrices consisting of the original and the transformed coordinates respectively, and letting L denote the linear transformation from one to the other, we have

This shows that V′ = V if the transformation L has unit determinant. Now, we know that L is strictly a function of the relative velocity v between the two systems of inertial coordinates, and by isotropy we know that the change in volume for a given speed does not depend on the direction, so we have |L(v)| = |L(−v)|. Furthermore, by reciprocity, if we apply the transformation for v and then apply the transformation for –v, we must arrive back at the same volume, which implies |L(v)| |L(-v)| = 1, and so |L(v)|² = 1. It follows that |L(v)| equals +1 or −1, but since |L(0)| = 1  we must have |L(v)| = 1, which completes the proof that the transformed spacetime volume of any defined region of spacetime is invariant under such a transformation.

It might seem as if a simpler form of this argument could be used to prove the invariance of almost anything. For example, suppose we assert that the spatial length factor ℓ relating the spatial length of a rod in two different coordinate systems, is a function of v, and by isotropy we have ℓ(v) = ℓ(-v), and by reciprocity we have ℓ(v)ℓ(-v) = 1, and therefore ℓ(v) = 1. However, this reasoning is invalid, because the ratio of spatial lengths for two frames is not purely a function of the velocity v between the frames. It also depends on the velocity of the rod relative to the initial frame, which cannot be inferred from the spatial length relative to that frame, precisely because spatial length is not an invariant. Thus the “proof” is based on the assumption of the very thing it sets out to prove, namely, the invariance of the subject attribute. The previous reasoning works for the spacetime volume only because, in that case, the given information is a set of vertices in terms of a given system of coordinates, and those vertices uniquely determine the spacetime volume of the region relative to those coordinates. We can then multiply the matrix of vertices by the transformation matrix, and use the fact that the latter has unit determinant to prove invariance of the volume. (The same argument could be applied to just the projected area based on the xt transformation, but the proof would be no simpler than the proof for the full spacetime volume.)

Of course, we couldn’t argue (as Abraham did for his constant-volume model) that the force preventing the electron from flying apart could be neglected because it does no work. We know (from the resolution of the “4/3” problem) that the Poincare force must be acknowledged to perform work. Moreover, the concept of work relies on variation of spatial volume with time, whereas the spacetime volume doesn’t vary with time. We’re accustomed to thinking that any invariant represents a physically significant quantity, and yet the significance of spacetime volume is unclear. One could argue that the only physical configurations that possess a well-defined spacetime volume are those that expand from and contract to singular spatial points. A stationary sphere, in contrast, has an infinite spacetime volume, and if we consider just a finite time-span of the sphere’s existence, there is an ambiguity in how the time slice is to be taken across the spatial extent of the sphere. But the sphere’s own rest frame could be taken as defining a distinguished time coordinate.

As a historical aside, it would be interesting to know if Poincare ever considered the similarity between (1) the universal pressure he posited to account for the apparent force of attraction holding together the separate parts of electrons, and (2) the Fatio-Lesage model of gravitation, which posited a universal pressure to account for the apparently attractive force of gravity. Poincare made a detailed study of the latter hypothesis, concluding that it was not viable on thermodynamic grounds, assuming the pressure was supplied by the impacts of either particles or waves. As far as I know, he never speculated about a mechanism for the Poincare pressure, which is usually described today as a negative pressure inside the electron, vanishing outside the electron, whereas (as shown in the quote given previously) Poincare originally presented it as an external pressure. Einstein wrote in 1919 a speculative paper about the possibility that gravitational fields play a role in the structure of elementary particles:

The scalar of curvature plays the part of a negative pressure which, outside of the electric corpuscles, has a constant value G₀. In the interior of every corpuscle there subsists a negative pressure (positive G – G₀) the fall of which maintains the electrodynamic force in equilibrium.

He also mentioned this in a letter to David Hilbert the same year, and again in his Princeton lectures (1921), where he explicitly mentioned Poincare by name in relation to this pressure:

Matter consists of electrically charged particles.  On the basis of Maxwell's theory these cannot be conceived of as electromagnetic fields free from singularities. In order to be consistent with the facts, it is necessary to introduce energy terms, not contained in Maxwell's theory, so that the single electric particles may hold together in spite of the mutual repulsions between their elements, charged with electricity of one sign. For the sake of consistency with this fact, Poincare has assumed a pressure to exist inside these particles which balances the electro-static repulsion. It cannot, however, be asserted that this pressure vanishes outside the particles. We shall be consistent with this circumstance if, in our phenomenological presentation, we add a pressure term. This must not, however, be confused with a hydrodynamical pressure, as it serves only for the energetic presentation of the dynamical relations inside matter… the physical nature of this pressure can be appreciated only after we have a better theoretical knowledge of the electromagnetic field.

Just four years later, quantum mechanics and then quantum field theory began to provide a “better theoretical knowledge of the electromagnetic field”, and the electron came to be regarded as a structureless point (or rather, as the quantum field corresponding to a point particle). This, as mentioned above, led Max Born to comment that “at present the tendency is to circumvent the problem of self-energy rather than to solve it. But one day it will return to the center of the scene.”

Return to MathPages Main Menu