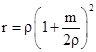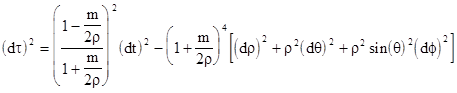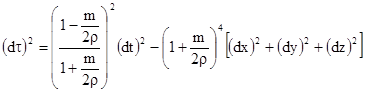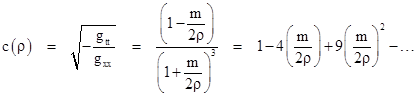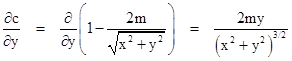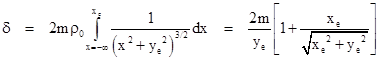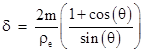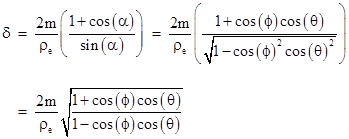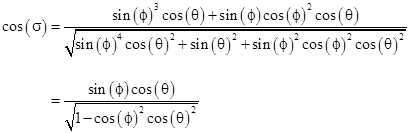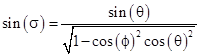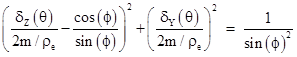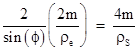Celestial Deflections

"I'm going to get out of this town," Nick said. "Yes," said George. "That's a good thing to do." "I can't stand to think about him waiting in the room and knowing he's going to get it. It's too damned awful." "Well," said George, "you better not think about it."

                                                                                              Ernest Hemingway, 1927

One of the earliest and most famous successes of general relativity was the correct quantitative prediction of the deflection of a beam of light in a gravitational field. During the early part of the 20^th century the only feasible opportunity for observing this effect was for beams of light grazing the Sun during a solar eclipse. The predicted deflection for this case can be computed by evaluating the asymptotic Sun-centered angles of the geodesic path of light, since the perigee of the path is extremely small (essentially just the radius of the Sun) compared with the distance to the receiver (the radius of the Earth’s orbit). We can use Schwarzschild coordinates to conveniently perform this evaluation, since central angles are represented in the usual way in terms of these coordinates. However, it’s worth noting that the rate of deflection along the trajectory of light varies in a peculiar way in these coordinates, because non-central angles are not related to the x and y coordinate differences in the usual way, due to the curvature of space. This is discussed in the article “Doubling the Deflection”.

The problem is that if we try to evaluate the angle of the light ray, not just asymptotically as the distance from the Sun increases to infinity (in which case we are dealing with central angles), but at some intermediate point along the trajectory, we are no longer dealing with a central angle, so we can’t express the actual physically measureable angle (between, say, the radial line from Sun to receiver and the trajectory of the light ray) in simple terms of the x and y coordinate increments.

To derive the deflection of light arriving at some arbitrary point (in the solar system) from an infinitely distant star, it is best to work in terms of isotropic coordinates. These are defined as the coordinates in terms of which the coordinate speed of light is isotropic at every point. Isotropic coordinates are more suitable for this purpose than Schwarzschild coordinates because angles are represented in the usual way in terms of isotropic coordinates (although distances are not). Beginning with the Schwarzschild coordinates t,r,θ,ϕ, we get isotropic coordinates t,ρ,θ,ϕ where the radial Schwarzschild coordinate r is related to the radial isotropic coordinate ρ by

In terms of the isotropic coordinates, the metric line element in a spherically symmetrical gravitational field is

If we define space coordinates x,y,z by

then the metric can be written as

We will first consider rays of light arriving in the solar system from a star located at infinite distance in the negative x direction, in the z = 0 plane of the Earth’s orbit. Following the analysis described in Doubling the Deflection, but now in terms of isotropic instead of Schwarzschild coordinates, we have the speed of light in the x direction as a function of radial distance from the Sun

Therefore, to the first order we have c(ρ) = 1 – 2m/ρ, and we have the partial derivative

For sufficiently small total deflection we can consider a virtually straight ray moving in the positive x direction at constant y = y_e. Using Huygens’ Principle, the total deflection (to first order) from an infinitely distant source to the point located at x_e, y_e is

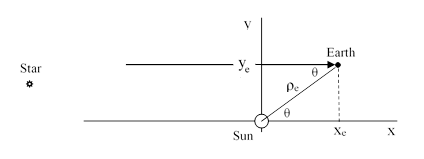
Let θ denote the angle between the incoming light ray and the line from the Earth to the Sun, and  ρ_e the radius of the Earth’s orbit (assumed circular) around the Sun, as shown in the figure below.

Making the substitutions

into the preceding expression for δ, we find that the gravitational deflection of the star light received on the Earth is (to the first order)

As expected, if θ approaches 0, so that the ray of light is just grazing the Sun, this deflection goes to 4m/ρ_s where ρ_s is the radius of the Sun. For other values of θ one might think the deflection would be too small to observe, but with Very Long Baseline Interferometry (VLBI) it is actually possible to discern the gravitational deflection in the light from stars at all positions in the celestial sphere, not just those appearing near the Sun. (Of course, in order to resolve such small effects, it is necessary to first account for all other effects, such as aberration, distortion in the Earth’s atmosphere, refraction due to the solar corona, and so on.)

It’s interesting to consider how the apparent position of a distant star or quasar (after correcting for all other effects) varies over the course of a year due to the gravitational field of the Sun as the Earth completes an orbit. In general, the stars are not located on the ecliptic plane. Let ϕ denote the angular elevation above the ecliptic of a certain star. The unit vector pointing from the Earth to that distant star, at constant y, is [-cos(ϕ),0,sin(ϕ)], and the unit vector pointing from the Earth to the Sun is [-cos(θ),-sin(θ),0]. The cosine of the angle α between these two unit vectors is their dot product, so we have

The angle α is to be substituted for θ in the prior equation for the deflection, so the magnitude of the deflection is

To determine the direction of this deflection  as seen from the Earth, we first note that the path of the light ray can be written parametrically in terms of a path length parameter s progressing from the Earth toward the star as

Differentiating the distance from this path to the origin, and setting the result to zero, we find that the point of closest approach is at s = cos(ϕ)x_e, so the vector from this point to the Sun is proportional to

Also, recall that the unit vector in the direction from Earth to star is [-cos(ϕ),0,sin(ϕ)], so a unit vector in the y = y_e plane that is perpendicular to the ray of light is [-sin(ϕ),0,-cos(ϕ)]. We take this latter vector as our reference direction, and the cosine of the angle σ between this reference vector and the vector from the perigee to the Sun is given by the dot product divided by the product of the magnitudes. Thus we have

It follows that

Therefore, letting dY denote the component of the deflection parallel to the ecliptic plane, and dZ the component perpendicular to the ecliptic plane, relative to the axis pointing directly to the star’s actual position, the components of the gravitational deflection are

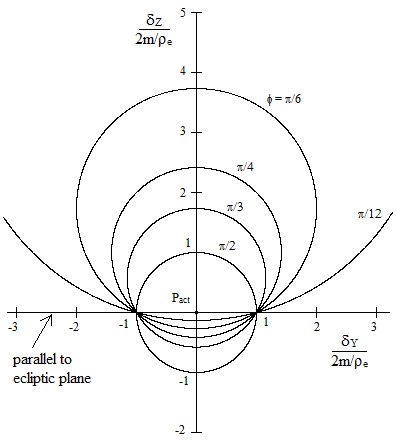
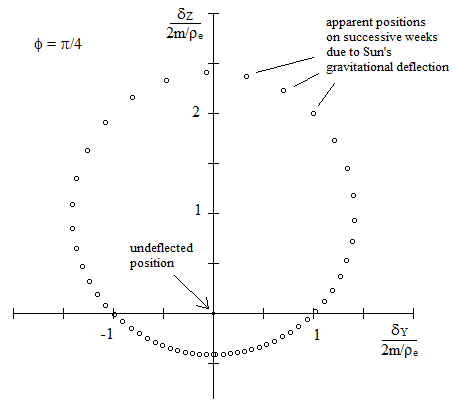
The apparent positions of the star throughout the year (as the Earth completes one circular orbit around the Sun) are shown below for various elevations ϕ of the star above the ecliptic plane.

Remarkably, the apparent position of the star traces out a perfect circle (as we show below). The actual position of the star, i.e., where it would appear without gravitational deflection, is at the coordinate origin point denoted by P_act in this figure. The case of ϕ = π/2 is for stars located in a direction normal to the Earth’s orbital plane (i.e., directly above the “North Pole” of the solar system), and in that case the deflection has the constant magnitude 2m/ρ_e, consistent with the fact that this is half the total asymptote-to-asymptote deflection for a ray whose nearest distance from the Sun is ρ_e, the radius of the Earth’s orbit.

The fact that the loci of apparent positions are perfect circles is confirmed by noting that

Thus the radius of the normalized circle is 1/sin(ϕ). This is consistent with the familiar expression for the deflection of a ray grazing the Sun, because for very small ϕ the bottom of the circle shows virtually no deflection and the top of the circle (when the star and Earth are nearly in opposition and the ray is just grazing the Sun) is at 2/sin(ϕ). Noting that the radius of the Sun ρ_S equals sin(ϕ)ρ_e in this configuration, the deflection is

as expected.

Naturally the apparent position of the star doesn’t move uniformly around the circle (except in the special case ϕ = π/2). For example, with ϕ = π/4, there is relatively little deflection during most of the year, and the deflection reaches its maximum value only when the star is closest to opposition. The figure below shows the sequence of apparent (normalized) positions for this case at one week intervals during the year.

Needless to say, this is an idealized analysis, since (for example) the Earth’s orbit is not perfectly circular. At the extreme levels of resolution achievable by VLBI it would likely be possible to discern various non-ideal effects. Also, we’ve assumed the total deflection is sufficiently small that we can integrate over an essentially straight ray.

Return to MathPages Main Menu