Acceleration and Gravitation in 1907

In Section 18 of his 1907 Jahrbuch survey article, Einstein discusses the relationship between clock rates at different locations in terms of what he calls accelerating systems of reference. He considers a standard system S of inertial coordinates, and another system Σ that is “uniformly accelerated” relative to S. This is slightly ambiguous, because he doesn’t specify whether it is constant coordinate acceleration or constant proper acceleration. However, for purposes of his discussion, the difference is insignificant, because he restricts his analysis to just the first order, and considers only incremental acceleration from a stationary condition. It should also be noted that Einstein is taking as the temporal foliation of the accelerating coordinate system the locus of time slices of the clock’s momentarily co-moving system of inertial coordinates, which he generically refers to as S′. Naturally this doesn’t yield a coherent foliation over arbitrary distances, since these slices intersect with each other at sufficient distance, but Einstein’s discussion focuses on the local region.

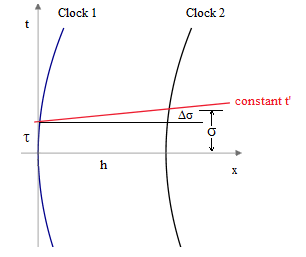
He begins by noting that if, at time t = 0 of the S coordinates, two clocks at separate locations on the x axis are synchronous with respect to S and thereafter undergo the same motions (i.e., equal velocities at equal t) along the x axis, they remain forever synchronous with respect to S. However, those clocks are not in general synchronous in terms of some other system S′ of standard inertial coordinates in terms of which the clocks may be stationary at a given time t′. Note that Einstein doesn’t consider that two separate accelerating clocks generally don’t share the same sequence of co-moving standard inertial coordinate systems, other than in the special case of Born rigid motion, which entails that the leading clock has slightly less proper acceleration than the trailing clock. However, this is a higher-order effect, and can be neglected for purposes of Einstein’s discussion, because he is focusing exclusively on the first-order effect of the tilting time slices, as depicted in the figure below.

Beginning from a time t=0 when both clocks were stationary and separated by a distance h, after the left hand clock has undergone an elapsed time of τ with an acceleration a, it has velocity v = aτ, and using geometrical units such that c=1, it follows from the Lorentz transformation that, to the lowest order of approximation, we have Δσ/h = v = aτ. Therefore, to the first approximation we have

At this point, Einstein notes that we could take as our origin any event along the trajectory, if the acceleration a is constant in terms of every S′ (which implies constant proper acceleration), and get a factor of this form for any increment, and hence we could split the increment into two equal parts and assert σ = τ(1 + ah/2)², or we could split into three equal parts and assert σ = τ(1 + ah/3)³, and in general for n parts we could assert σ = τ(1 + ah/n)ⁿ, in the limit as n increases indefinitely, which leads to Einstein’s conclusion that, strictly speaking, the relation should be

This differs from the previous expression only in higher orders, but recall that the previous expression was derived by expressly neglecting terms of higher than first order, so it can’t really serve as the basis for inferring a putative exact expression. To give an exact result for a finite interval (as decribed in another note), we must specify the exact trajectories of the two clocks in terms of some specific system of coordinates, including whether the trajectories maintain constant proper separation (like the ends of an object in Born rigid motion) or constant coordinate separation (like two independent objects subjected to identical proper accelerations). It is then straightforward to deduce the exact result for any specified situation. Likewise for two clocks that are stationary at different elevations in terms of, say, Schwarzschild coordinates near a spherically symmetrical gravitating body, we can deduce the exact expression for the gravitational time dilation.

Among well-known texts, only Rindler repeats Einstein’s exponential form, which he does by (again) neglecting some higher order terms and asserting the classical first-order Doppler shift dv for an incremental change dh in elevation given by 1 + νdν/ν = 1 + a dh, from which he gets dν/ν = ah, and hence by integration ν₂/ν₁ = e^aΔh, which corresponds to the ratio σ/τ of time intervals (periods).

In his 1907 paper Einstein goes on to assert the equivalence between the above situation and two clocks resting at different elevations in a “homogeneous gravitational field”, equating the quantity aΔh with the difference in gravitational potential. It’s interesting that, even at this early stage in his development of general relativity, he carefully points out the different possible choices of coordinate systems, and notes the special significance of the system in terms of which “the laws of nature can vary with position but not with time”. In other words, in a gravitational field we ordinarily prefer the essentially unique temporal foliation (such as the coordinate time t of Schwarzschild coordinates in a spherically symmetrical field) in terms of which the metric coefficients are independent of the time coordinate.

In §17 Einstein asks us to consider two “systems” (presumably of space and time coordinates), one in flat spacetime undergoing constant acceleration a, and the other stationary in a homogeneous gravitational field that imparts to all objects an acceleration –a. He proposes that the laws of physics expressed in terms of these two systems are identical.

There are already some difficulties in what has been stated there. For one, even in flat spacetime the concept of an accelerating system of space and time coordinates is fraught, because there is no such thing as a rigid accelerating grid in special relativity. For another, the concept of a homogeneous gravitational field in general relativity is inherently problematic. In Newtonian theory under Galilean relativity, the gravitational acceleration due to an infinite flat wall is constant at all distances from the wall, and similarly it is possible to have a perfectly rigid accelerating grid of any size in the absence of gravity. However, in general relativity, neither of these things are true.

In 1907 Einstein obviously didn’t know general relativity, but he was in a position to know that there can be no perfectly rigid accelerating bodies or reference frames in special relativity. In §18 he restricts his discussion to sufficiently low accelerations and considers only the lowest order terms. He considers two clocks separated by a distance L and both undergoing the same constant acceleration a, and he assets that the distances between the clocks remain constant, and that the ratio of the clock rates for the leading and trailing clocks is (to the lowest order) 1 + La.

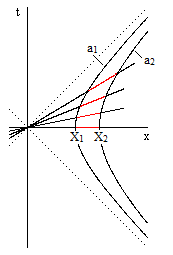
To determine the exact answer, we must consider the case of two clocks accelerating in Born rigid motion, i.e., imagine them attached to the ends of a rod of proper length L undergoing Born rigid constant proper acceleration such that the trailing clock has constant proper acceleration a₁.  (See also Accelerated Travels.) This is depicted in the figure below.

As discussed in the referenced articles, working in geometrical units (so c=1), the elapsed proper time for the trailing clock from the time when it had zero velocity is

where X₁ is the constant distance of the trailing clock from the hyperbolic fulcrum event, and v is the velocity of the clock in terms of the original inertial coordinate system. Likewise the elapsed proper time for the leading clock from the time when it had zero velocity is

We have X₂ – X₁ = L, and the derivatives of the proper times with respect to v (simultaneous in terms of the common inertial coordinates in which the clocks are momentarily at rest) are

Accordingly we have the ratio of the proper time rates (matched with this co-moving simultaneity)

Thus the ratio of proper time rates equals the ratio of distances to the fulcrum, and equals the reciprocal of the ratio of accelerations. Since X₂ = X₁ + L, this implies

If we have a row of clocks, separated by L and subjected to aggregate Born rigid motion, the ratios of the proper time rates mapped by the co-moving inertial foliation for consecutive clocks are 1 + a₁L, 1 + a₂L, 1 + a₃L, … and so on, where the accelerations are in descending order. In Einstein’s paper he was working with the mutually contradictory premises that the proper distances between consecutive clocks were constant and they all had equal constant proper acceleration a, so he thought the ratio of rates for consecutive clocks were all 1 + aL. If this were true, then the ratios of proper times to the rate at the origin would have to increase exponentially, and to match the lowest order expression in the limit we must have dτ₂/dτ₁ = e^ax. However, as noted, this was based on the mutually exclusive premises of equal proper accelerations and constant proper distance in terms of the relevant coherent temporal foliation (which requires Born rigid motion). Fortunately, Einstein confined himself to the lowest order expression, and made no use of the exponential expression.

Einstein then turned his attention to gravitational fields, commenting that, by his proposed equivalence, we should find that a clock at higher elevation in a (assumed uniform) gravitational field where the gravitational potential differs from the potential at the origin by the amount Φ = aL should “run faster” by the ratio 1 + Φ. He then carefully explains that this comparison of rates is based on the simultaneity mapping of a stationary system of coordinates, in terms of which the expressions of the laws of physics may differ at different locations, but not at different times.

Ironically, significant gravitational fields of our experience are ordinarily produced by a large and roughly spherical mass, so two stationary clocks at different elevations will actually have different “proper” accelerations, just as we find for clocks in Born rigid motion in flat spacetime. However, there aren’t enough degrees of freedom to match the relations for an arbitrary spherical gravitational field over any extended region. As Einstein continued to develop general relativity it became clear that the equivalence principle is a differential principle that applies to the functions and first derivatives at any given event, rather than over extended regions.

Return to MathPages Main Menu